
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка и анализ результатов измерений.Содержание книги
Поиск на нашем сайте 1. Заполнить таблицу 1.1, вычислив средние значения угла φ2, а также по формуле (1.17) коэффициент восстановления 2. Определить, какая часть первоначальной кинетической энергии переходит в другие виды энергии по формуле:
3. Вычислить среднее значение времени соударения и по формуле (1.16) значение скорости первого шара до удара для каждого угла 4. Записать массу шара т. Вычислить для каждого угла
Результаты занести в таблицу 1.2. 5. Построить графики зависимости времени соударения τ и средней силы взаимодействия F ср от относительной скорости шаров до удара v отн = v 01. 6. Определить вид зависимости времени соударения τ от относительной скорости шаров v отн. Для этого построить график зависимости lgτ = f (lg v отн). Если график представляет собой прямую линию, то lgτ = b ·lg v отн + const, где b − тангенс угла наклона графика к оси, на которой отложен lg v отн. Из графика определить значение b и записать зависимость τ от v отн в виде Контрольные вопросы 1. Какие виды ударов вы знаете? Дайте их краткую характеристику. 2. Что называется коэффициентом восстановления? От чего он зависит? Назовите основные источники погрешностей измерений коэффициента восстановления. 3. Напишите физические законы, которые используются для вывода формул скоростей шаров при центральном ударе. 4. Запишите формулу второго закона динамики в импульсной форме. Каков физический смысл величин, входящих в эту формулу? 5. Как определяется по контактной теории время соударения двух одинаковых шаров при центральном ударе?
Литература: [ 1, § 16, 23, 24, 25]; [ 2, § 18, 26, 28, 29]; [ 4, § 5.1, 5.2]; [ 5 ]
Лабораторная работа № 2
Определение коэффициента трения качения
Цель работы – экспериментальное нахождение коэффициента трения качения при помощи наклонного маятника. Приборы и принадлежности: наклонный маятник FPM-07.
Краткие сведения из теории
Всякое движущееся тело встречает сопротивление своему движению со стороны окружающей его среды и других тел, с которыми оно во время движения соприкасается. Иначе говоря, на любое движущееся тело действуют силы трения или силы сопротивления. В результате их действия всегда происходит превращение механической энергии во внутреннюю энергию трущихся тел, т.е. в энергию теплового движения их частиц. Силы трения имеют электромагнитную природу и связаны с межмолекулярным взаимодействием тел, но в механике останавливаются на эмпирических законах трения, которые зачастую являются довольно грубыми приближениями. Силы трения между взаимодействующими телами зависят не только от взаимного расположения, но и от их относительной скорости Остановимся на классификации сил трения. Трение называют внешним, если оно действует между различными соприкасающимися телами, не образующими единого тела (брусок на наклонной плоскости). Внутреннее трение проявляется между отдельными частями одного и того же тела (слои газа или жидкости). Трение между поверхностью твердого тела и жидкостью или газом, в котором оно движется, называют вязким. Трение между поверхностями твердых тел называют сухим. Оно делится на трение скольжения и трение качения. Сухое трение (в отличие от вязкого) не исчезает при обращении в ноль относительных скоростей соприкасающихся тел (трение покоя). Существует максимальное значение трения покоя f 0. Если брусок будет двигаться со скоростью v, то сила трения будет зависеть от скорости. Она не зависит тот площади поверхности контакта и пропорциональна силе нормального давления f n, с которой одно тело действует на другое. F тр = μ f n Коэффициент μ называют коэффициентом трения. Если речь идёт о трении скольжения, то μ – коэффициент трения скольжения. Трение качения возникает между шарообразным или цилиндрическим телом, катящимся без скольжения по плоской или изогнутой поверхности. Трение качения описывается теми же законами, что и трение скольжения, но коэффициент трения при качении во много раз меньше, чем при скольжении. Если тело катится без проскальзывания, то скорость точек касания поверхности равна нулю, а, значит, сила трения качения работы не совершает. Это справедливо, если при качении не возникают деформации, как самого тела, так и поверхности, по которой оно катится. Но при возникновении деформаций сила трения качения совершает отрицательную работу и кинетическая энергия тела уменьшается. Убыль этой энергии идет на преодоление сил трения. Рассмотрим перераспределение сил, действующих на катящееся тело при возникновении деформаций.
Рис. 2.1 При качении по плоской поверхности шара возникают деформации. Поэтому точка А приложения силы F R реакции поверхности несколько смещается вперед, а линия действия силы отклоняется от вертикали назад (рис.2.1). Нормальная составляющая реакции F R п = – mg, а касательная составляющая F Rτ и является силой качения: F кач = F Rτ. При равномерном качении сила F кач компенсируется силой тяги F, а реакция F R направлена вдоль прямой АО, так что ее момент относительно, оси симметрии катящегося тела равен нулю. Если R – радиус шара, а f к величина смещения точки А приложения реакции, то из условия равенства нулю момента силы относительно оси 0 следует, что F кач · R = F R п · f к = mg · f к. Поэтому для силы трения качения справедлив закон Кулона: F кач = f к · Величину f к называют коэффициентом трения качения k тр.
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

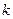 для каждого значения угла
для каждого значения угла 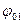 . Найти среднее значение коэффициента восстановления и оценить погрешность определения
. Найти среднее значение коэффициента восстановления и оценить погрешность определения 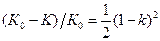
 от центра шара до оси вращения.
от центра шара до оси вращения.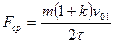
 ~
~ 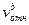 . Полученную формулу сравнить с формулой (1.15). Сделать вывод о соответствии результатов опыта с контактной теорией удара.
. Полученную формулу сравнить с формулой (1.15). Сделать вывод о соответствии результатов опыта с контактной теорией удара.
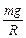 .
.


