Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка экспериментальных данныхСодержание книги Поиск на нашем сайте 1. По формуле (8.8) вычислить коэффициент крутильной жесткости k. 2. По данным таблицы 8.1 для каждого измерения вычислить период колебаний 3. Усреднить значения 4. По данным таблицы 8.2 вычислить периоды колебаний 5. Вычислить по формуле (8.7) моменты инерции образца Ii относительно осей x, y, z и AB. Для каждой из осей усреднить полученные значения Ii, оценить погрешность по разбросу значений и записать окончательный результат. 6. Провести оценочные расчёты моментов инерции Ii выбранного образца (параллелепипеда) без учёта скоса вершин относительно осей x, y, z и AB по формулам (8.1 – 8.4). При расчетах использовать следующие данные:
7. Сравнить результаты п. 4 с опытными данными (результатами п. 3). Контрольные вопросы
1. Уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси. 2. Что называется моментом инерции твёрдого тела? 3. Выведите формулу для момента инерции однородного прямоугольного параллелепипеда относительно оси x (рис. 8.3). 4. Сформулируйте теорему Штейнера.
Литература: [ 1, § 13, 27, 28, 31, 32]; [ 2, § 33-36, 46, 79]; [ 4, § 4.1-4.3 ]; [ 5 ]. Лабораторная работа №9 ОПРЕДЕЛЕНИЕ МОДУЛЯ КРУЧЕНИЯ НИТИ И МОМЕНТА ИНЕРЦИИ СИСТЕМЫ, СОВЕРШАЮЩЕЙ КРУТИЛЬНЫЕ КОЛЕБАНИЯ
Цель работы – определение момента инерции крутильного маятника и модуля кручения нити по результатам исследования неупругого соударения математического и крутильного маятников. Приборы и принадлежности: крутильный маятник, математический маятник, секундомер.
Краткие сведения из теории
Крутильным маятником называется твёрдое тело, подвешенное на упругой нити, которое может совершать колебания вращательного характера под воздействием момента упругих сил, возникающих в нити. В работе используется маятник с большим периодом собственных колебаний T0. Предположим, что под кратковременным воздействием внешней силы (tдейств<< T0) маятник выведен из положения равновесия. Нить, на которой подвешен маятник, закрутится. Пи этом возникнет момент упругих сил, возвращающих маятник в начальное положение: Мкр= – kj, (9.1) где j – угол закручивания нити; k – модуль кручения нити, численно равный величине крутящего момента относительно оси вращения, приходящегося на единичный угол закручивания (в литературе можно встретить другое название этой величины – крутильная жесткость нити). Знак «–» говорит о том, что направление крутящегося момента сил упругости противоположно направлению угла закручивания. Тогда уравнение вращательного движения маятника относительно неподвижной оси ОО 1 (рис 9.2) с учётом (9.1) можно записать
где I – момент инерции маятника относительно оси вращения; Если обозначить
то уравнение движения крутильного маятника (9.2) можно переписать так: Циклическая частота связана с периодом свободных колебаний маятника
Принимая во внимание, что угловая скорость вращательного движения
В качестве тела, воздействующего на исследуемый крутильный маятник, можно использовать математический маятник – массивный шарик, подвешенный на лёгком, нерастяжимом стержне длиной l (при этом rш<<l, mш>> mподвеса). Математический маятник совершает колебания в вертикальной плоскости под действием возвращающей силы F= mgsin β0 (рис.9.1).
Рис. 9.1 Если маятник отклонить от положения равновесия на угол β0 ( или поднять на высоту h), то скорость шарика в нижней точке траектории можно оценить по закону сохранения энергии mgh = m
Исследуемый крутильный маятник представляет собой два металлических стержня, сцеплённых между собой так, чтобы угол между ними был равен 90° (рис.9.2). На концах горизонтального стержня укреплены два диска, расположенные в вертикальной плоскости. Выведенный из положения равновесия шарик ударяется о диск Д2, приводя крутильный маятник в колебание. После соударения о диск скорость шарика становится равна
где Для системы «крутильный маятник – математический маятник» применим закон сохранения момента импульса относительно неподвижной оси ОО 1. До удара момент импульса системы равен моменту импульса математического маятника относительно оси вращения ОО 1 L0=mv0r, где r – расстояние от оси крутильного маятника до точки удара шарика о диск; v0 – скорость шарика перед ударом; m – масса шарика. После соударения момента импульса шарика относительно оси L = – mvк r, где vк – скорость шарика после удара. Момент импульса крутильного маятника относительно оси сразу после соударения, с учетом (9.5) равен: Lкр = Iwmax = I Таким образом, закон сохранения момента импульса системы запишется: mv0r = – mvк r + I Найдем из этого равенства момент инерции крутильного маятника: I= Подставив в это выражение (9.6) и (9.7), получим:
Это соотношение является рабочим для расчёта момента инерции крутильного маятника. (При расчётах Масса шарика m, длина подвеса l и расстояние r от оси крутильного шарика до точки соприкосновения с шариком при ударе указаны на установке.
Описание экспериментальной установки
Рис. 9.2 Крутильный маятник состоит из двух взаимно перпендикулярных стержней. Вертикальный стержень с двух сторон жестко соединён с упругой вертикальной нитью, модуль кручения которой нужно определить. На горизонтальном стержне, кроме дисков Д имеются цилиндры С, положение которых можно менять, передвигая их вдоль стержня. Изменение положений цилиндров С относительно оси вращения крутильного маятника приводит к изменению момента инерции всей системы. К центру горизонтального стержня прикреплён указатель К1, при помощи которого можно измерять углы поворота Математический маятник представляет собой маятник известной массы m, подвешенный на лёгком стержне длиной l. С шариком скреплён указатель К2, перемещающийся по вертикальной шкале Ш2. Шкала Ш2 разделена на градусы, по ней определяются углы отклонения шарика от положения равновесия Крутильный и математический маятники расположены так, чтобы выведенный из положения равновесия шарик ударялся о диск крутильного маятника в момент, когда скорость шарика направлена горизонтально.
Порядок выполнения работы
1. Проверить, что указатели углов К1 и К2 находятся на нулевом делении. 2. Цилиндры С разместить вплотную к дискам Д1 и Д2 и закрепить их. 3. Отклонить математический маятник на угол 4. Отклонить шарик математического маятника на тот же угол
I ср=……….. 5. Лёгким толчком по диску Д2 привести крутильный маятник в движение. Измерить по секундомеру время десяти полных качаний маятника и вычислить период собственных колебаний T0 = ti / 10. 6. Для каждого из пяти значений 7. По среднему значению момента инерции Iср, пользуясь формулой (9.4), определить модуль кручения нити k. 8. Цилиндры С переместить вплотную к вертикальному стержню крутильного маятника. Повторить п.п. 2-7. Данные занести в таблицу, аналогичную табл. 9.1. 9. Подсчитать погрешность полученных значений моментов инерции как погрешность прямых изменений. Погрешность измерения модуля кручения подсчитать по правилам оценки погрешности косвенных измерений.
Контрольные вопросы и задания 1. Дайте определение момента инерции и момента импульса материальной точки и твёрдого тела. 2. От чего зависит момент инерции абсолютно твёрдого тела? 3. Сформулируйте закон сохранения момента импульса. 4. Запишите законы сохранения для абсолютно упругого соударения для системы «крутильный маятник – математический маятник». 5. От чего зависит модуль кручения?
Литература: [ 1, § 13, 28, 31, 32]; [ 2, § 33-36, 46, 79]; [ 4, § 4.1-4.3, 27.1, 27.2]; [ 5 ].
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 945; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 и момент инерции рамки
и момент инерции рамки  по формуле (8.6).
по формуле (8.6). относительно различных осей.
относительно различных осей.
 , (9.2)
, (9.2)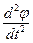 – угловое ускорение вращательного движения относительно оси вращения; Уравнение (9.2) справедливо для углов
– угловое ускорение вращательного движения относительно оси вращения; Уравнение (9.2) справедливо для углов  < 30°, когда
< 30°, когда 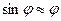 .
.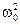 = k/I, (9.3)
= k/I, (9.3)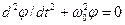 . Решение данного дифференциального уравнения ищем в виде
. Решение данного дифференциального уравнения ищем в виде  , где
, где  – амплитудное значение угла закручивания; a – начальная фаза колебаний,
– амплитудное значение угла закручивания; a – начальная фаза колебаний,  – циклическая частота собственных колебаний маятника.
– циклическая частота собственных колебаний маятника. формулой
формулой  , тогда с учётом (9.3) модуль кручения нити можно выразить
, тогда с учётом (9.3) модуль кручения нити можно выразить (9.4)
(9.4) , получаем
, получаем  . Очевидно, что максимальное значение угловой скорости вращения маятника равно
. Очевидно, что максимальное значение угловой скорости вращения маятника равно . (9.5)
. (9.5)
 . С учётом h = l – l cosβ0 = l(1 – cosβ0 ) = 2 l sin2β0/2 (рис.9.1) получаем
. С учётом h = l – l cosβ0 = l(1 – cosβ0 ) = 2 l sin2β0/2 (рис.9.1) получаем (9.6)
(9.6) (9.7)
(9.7)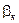 - угол отклонения математического маятника после удара.
- угол отклонения математического маятника после удара. ,
,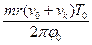
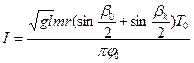 (9.8)
(9.8)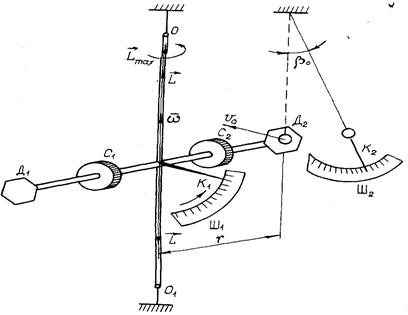
 крутильного маятника. Указатель К1 перемещается по шкале Ш1, проградуированной в градусах (рис.9.2).
крутильного маятника. Указатель К1 перемещается по шкале Ш1, проградуированной в градусах (рис.9.2).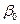 и
и 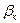 .
.
 в диапазоне 15° – 20° и отпустить его. Сразу же после удара о диск Д2 отвести горизонтальный стержень крутильного маятника в сторону для того, чтобы диск Д2 не мешал шарику совершать свободные колебания. По шкале Ш2 измерить амплитудное значение угла
в диапазоне 15° – 20° и отпустить его. Сразу же после удара о диск Д2 отвести горизонтальный стержень крутильного маятника в сторону для того, чтобы диск Д2 не мешал шарику совершать свободные колебания. По шкале Ш2 измерить амплитудное значение угла 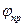 и
и  ). Опыт повторяют пять раз. Результаты измерений занести в табл.9.1.
). Опыт повторяют пять раз. Результаты измерений занести в табл.9.1. ……. Таблица 9.1
……. Таблица 9.1