
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффициента упругости (жесткости) пружиныСодержание книги
Поиск на нашем сайте
Груз, подвешенный на пружине, вызывает ее деформацию. Если пружина способна восстановить первоначальную форму, то ее деформация называется упругой. При упругих деформациях выполняется закон Гука:
где Fупр ¾ сила упругости; k ¾ коэффициент упругости (жесткость); D l - удлинение пружины. Примечание: знак “-” определяет направление силы упругости. Если груз находится в равновесии, то сила упругости численно равна силе тяжести: k D l = m g, тогда можно найти коэффициент упругости пружины:
где m ¾ масса груза; g ¾ ускорение свободного падения.
При последовательном соединении пружин (см. рис.1) силы упругости, возникающие в пружинах, равны между собой, а общее удлинение системы пружин складывается из удлинений в каждой пружине. Коэффициент жесткости такой системы определяется по формуле:
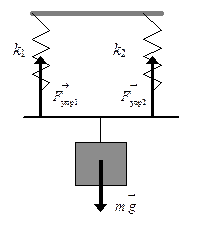
где k 1 — жесткость первой пружины; k 2 — жесткость второй пружины. При параллельном соединении пружин (см. рис. 2) удлинение пружин одинаково, а результирующая сила упругости равна сумме сил упругости в отдельных пружинах. Коэффициент жесткости при параллельном соединении пружин находится по формуле: k рез = k 1 + k 2. (3)
Порядок выполнения работы
1. Прикрепить пружину к штативу. Подвешивая к каждой пружине грузы в порядке возрастания их массы, измерять удлинение пружины D l. 2. По формуле F = mg рассчитать силу упругости. 3. Построить графики зависимости силы упругости от величины удлинения пружины. По виду графиков определить выполняется ли закон Гука. 4. По формуле (1) рассчитать коэффициент упругости пружины. Найти среднее арифметическое значение k ср. 5. Найти абсолютную погрешность каждого измерения D ki = ê ki - k ср ê. 6. Найти среднее арифметическое значение абсолютной погрешности D k ср. 7. Результаты измерений и расчетов занести в таблицу.
1. Провести измерения (как описано в задании 1) и рассчитать коэффициенты упругости последовательно и параллельно соединенных пружин. 2. Найти среднее значение коэффициентов и погрешности их измерений. Результаты измерений и вычислений занести в таблицу. 3. По формулам (2) и (3) рассчитать теоретические значения коэффициентов упругости при последовательном и параллельном соединении пружин. 4. Найти погрешность эксперимента, сравнив теоретические значения коэффициента упругости с экспериментальными по формуле:
Контрольные вопросы Сформулируйте закон Гука. Дайте определение деформации, коэффициента упругости. Назовите единицы измерения этих величин в СИ. Как находится коэффициент упругости для параллельного и последовательного соединения пружин? Лабораторная работа № 1-5 Изучение законов динамики Поступательного движения
Теоретические сведения Динамика изучает причины, вызывающие механическое движение. Инерция — способность тела сохранять состояние покоя или прямолинейного равномерного движения, если на это тело не действуют другие тела. Масса m (кг) — количественная мера инертности тела. Первый закон Ньютона: Существуют такие системы отсчета, в которых тело находится в состоянии покоя или прямолинейного равномерного движения, если на него не действуют другие тела. Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными. Сила Принцип суперпозиции сил: Если на материальную точку действуют одновременно силы
Импульс тела
Второй закон Ньютона:
где Замечание. Если масса тела постоянна, то второй закон Ньютона принимает вид:
где Сила тяжести Вблизи поверхности Земли тело массой m под действием силы тяжести
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 2933; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |

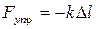 ,
,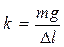 , (1)
, (1)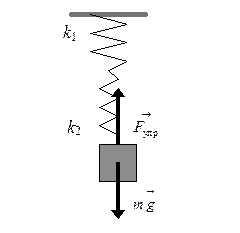
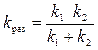 , (2)
, (2)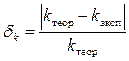 .
.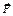 (Н) — векторная величина, характеризующая взаимодействие между телами или частями тела.
(Н) — векторная величина, характеризующая взаимодействие между телами или частями тела. и
и 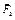 , то их можно заменить равнодействующей силой
, то их можно заменить равнодействующей силой 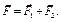
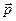 (кг∙м/с) — векторная величина, равная произведению массы m материальной точки на его скорость
(кг∙м/с) — векторная величина, равная произведению массы m материальной точки на его скорость 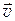 :
: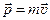 ,
,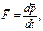
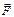 — равнодействующая сила, действующая на материальную точку.
— равнодействующая сила, действующая на материальную точку.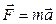 ,
,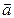 — ускорение, приобретаемое телом массой m под действием силы
— ускорение, приобретаемое телом массой m под действием силы 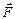 .
.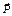 — сила, действующая на тело вследствие его притяжения к Земле или другим небесным телам.
— сила, действующая на тело вследствие его притяжения к Земле или другим небесным телам.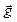 . Поэтому по второму закону Ньютона сила тяжести равна:
. Поэтому по второму закону Ньютона сила тяжести равна: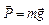 .
.


