
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упражнение 1. Измерение ускорения грузовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. После нажатия кнопки "ПУСК" подключите к сети лабораторную установку нажатием кнопки "СЕТЬ". На табло "ВРЕМЯ, С" должны появиться нули. Отожмите кнопку "ПУСК". 2. Установите средний кронштейн 7 на некотором расстоянии L2 от нижнего кронштейна 5. Измерьте L2 и расстояние L между верхним 6 и нижним 5 кронштейнами. Результаты измерений запишите в таблицу 1. 3. Опустите левый груз на нижний кронштейн. Добейтесь, чтобы нижняя грань правого груза совпадала с чертой на верхнем кронштейне. 4. Найдите массы груза М и перегрузка m. 5. Поместите перегрузок на правый груз. Таблица 1
6. Устранив возможные колебания грузов, нажмите кнопку "ПУСК" до ее фиксирования. 7. После остановки грузов запишите в таблицу 1 время t равномерного движения грузов, измеренное миллисекундомером и показанное на табло "ВРЕМЯ, С". 8. Нажмите кнопку "СБРОС". 9. Повторите пункты 2¸8 не менее четырех раз, меняя расстояние L2 между средним и нижним кронштейнами. 10. Для каждого измерения вычислите величины Если формула 11. Найдите величину ускорения а по методу наименьших квадратов:
где Результат измерения а: а ± D а. Используя найденные значения а и с, постройте на графике с экспериментальными точками прямую линию у = а х + с.
Упражнение 2. ИЗМЕРЕНИЕ УСКОРЕНИЯ
12. Определите величину ускорения свободного падения g по формуле
Полуширину доверительного интервала Dg найдите с помощью формулы:
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте цель лабораторной работы. 2. Что называется системой отсчета? 3. Дайте определение материальной точки. 4. Сравните понятия пути и перемещения. 5. Дайте определения средней и мгновенной скоростей. 6. Дайте определения среднего и мгновенного ускорений. 7. Как зависит траектория движения от направления ускорения? 8. Укажите формулы, связывающие кинематические величины при равноускоренном прямолинейном движении. 9. Дайте определение силы. 10. Что характеризует масса тела? 11. Сформулируйте основные законы динамики - законы Ньютона. 12. Какая система тел называется изолированной? 13. Сформулируйте законы сохранения импульса и механической энергии. 14. Какое движение тела называется свободным падением? 15. Как записать 2-ой закон Ньютона для свободного падения? 16. Как ускорение свободного падения зависит от широты точки наблюдения? 17. Почему величина ускорения свободного падения на уровне моря различна на полюсе и экваторе? 18. Как уменьшится ускорение свободного падения при подъеме с уровня моря на высоту h = 10 км? Радиус Земли R3=6370 км. 19. Нарисуйте эскиз машины Атвуда. 20. При каком условии ускорения тел, используемых в машине Атвуда, одинаковы по модулю? 21. При каких условиях одинаковы силы натяжения нитей по обе стороны неподвижного блока? 22. Как движется система тел в машине Атвуда? 23. Какое время измеряет секундомер машины Атвуда? 24. Укажите зависимость квадрата скорости равноускоренного движения системы тел от величины перемещения. 25. Какие величины определяют с помощью прямых измерений в данной лабораторной работе? 26. Какие сделаны допущения при выводе формулы ускорения системы тел? 27. По какой формуле определяют величину ускорения свободного падения g? 28. Найдите ускорение свободного падения, если масса 29. По какой формуле можно найти полуширину доверительного интервала Dg ускорения свободного падения? 30. Можно ли использовать закон сохранения механической энергии для описания движения системы тел в машине Атвуда? Лабораторная работа №2 ИЗУЧЕНИЕ АБСОЛЮТНО НЕУПРУГОГО УДАРА
ЦЕЛЬ РАБОТЫ
Изучение абсолютно неупругого удара. Оценка действующих сил и величины необратимых потерь механической энергии при абсолютно неупругом ударе.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Материальной точкой называется тело, размеры которого много меньше масштаба движения. В дальнейшем в этом пункте под словом "тело" следует подразумевать материальную точку. Силы, действующие на тела механической системы, можно разделить на две группы: 1) внешние силы 2) внутренние силы
Система тел называется изолированной или замкнутой, если на тела системы не действуют внешние силы, т.е. Если ускорение
где Рассмотрим систему двух тел с массами m1 и m2. Пусть тела системы взаимодействуют с силами
Складывая уравнения (3) и (4) и учитывая равенство (1), получим
Из уравнения (5) следует закон сохранения импульса: если система является изолированной (
Изменение скорости
где Импульсами внешних сил, например, сил тяжести, а также перемещениями тел за малое время удара Dt можно пренебречь. В этом случае уравнения (3) и (4) принимают вид:
Складывая уравнения (3¢) и (4¢) с учетом (1), получим уравнение (6), т.е. при кратковременных взаимодействиях даже в неизолированных системах закон сохранения импульса приближенно выполняется. Удар называется абсолютно неупругим, если после удара скорости тел одинаковы:
Изменение кинетической энергии тел при абсолютно неупругом ударе равно
Для кратковременного удара изменениями положения тел и их потенциальной энергии Ер можно пренебречь: DЕр = 0. Так как DЕk < 0, то полная механическая энергия тел убывает, переходя в другие виды энергии. Удар, при котором полная механическая энергия тел сохраняется, называется абсолютно упругим. Закон сохранения механической энергии можно сформулировать так: полная механическая энергия системы тел сохраняется, если система изолирована и на тела системы не действуют внутренние диссипативные силы (например, силы трения).
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.161.57 (0.007 с.) |

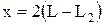

 и
и  , запишите результаты в таблицу 1 и постройте экспериментальные точки на графике, откладывая по оси абсцисс значения х, а по оси ординат - у.
, запишите результаты в таблицу 1 и постройте экспериментальные точки на графике, откладывая по оси абсцисс значения х, а по оси ординат - у. справедлива, то экспериментальные точки лежат на прямой, тангенс угла наклона которой определяет величину ускорения а грузов с перегрузком.
справедлива, то экспериментальные точки лежат на прямой, тангенс угла наклона которой определяет величину ускорения а грузов с перегрузком. ;
;  ;
; ;
; ;
;  ,
, - коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы
- коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы 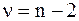 .
. .
. .
. , с которыми на тело с номером i действуют тела, не вошедшие в систему;
, с которыми на тело с номером i действуют тела, не вошедшие в систему; взаимодействия тел системы с номерами i и k. По третьему закону Ньютона:
взаимодействия тел системы с номерами i и k. По третьему закону Ньютона: или
или  . (1)
. (1) .
. записать в виде
записать в виде  ,
,  - малое изменение скорости тела за малый промежуток времени Dt, то второй закон Ньютона принимает вид
- малое изменение скорости тела за малый промежуток времени Dt, то второй закон Ньютона принимает вид или
или  , (2)
, (2) - начальная скорость тела;
- начальная скорость тела;  - конечная скорость спустя малый промежуток времени Dt. Величина
- конечная скорость спустя малый промежуток времени Dt. Величина  - импульс тела, а
- импульс тела, а  - импульс силы.
- импульс силы. и
и  и на тела действуют внешние силы
и на тела действуют внешние силы  и
и  . Запишем уравнение (2) для каждого тела системы:
. Запишем уравнение (2) для каждого тела системы: ; (3)
; (3) . (4)
. (4) . (5)
. (5) ;
;  ), то суммарный импульс тел такой системы сохраняется, т.е.
), то суммарный импульс тел такой системы сохраняется, т.е. . (6)
. (6) соударяющихся тел может быть достаточно большим, а время удара Dt очень мало (
соударяющихся тел может быть достаточно большим, а время удара Dt очень мало ( с). Поэтому ускорения тел и внутренние или ударные силы
с). Поэтому ускорения тел и внутренние или ударные силы  во время удара могут быть очень большими. Эти силы значительно превосходят внешние силы:
во время удара могут быть очень большими. Эти силы значительно превосходят внешние силы:  . Мерой механического воздействия на тело за время удара является импульс
. Мерой механического воздействия на тело за время удара является импульс  ударной силы
ударной силы  ,
, - средняя ударная сила за время Dt.
- средняя ударная сила за время Dt. ; (3¢)
; (3¢) . (4¢)
. (4¢)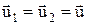 . Для такого удара уравнение (6) принимает вид
. Для такого удара уравнение (6) принимает вид .
. . (7)
. (7)


