
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава II. Механика материальной точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ГЛАВА II. МЕХАНИКА МАТЕРИАЛЬНОЙ ТОЧКИ Лабораторная работа №1 ИССЛЕДОВАНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ
ЦЕЛЬ РАБОТЫ Изучение равнопеременного и равномерного прямолинейных движений в поле земного тяготения. Определение ускорения свободного падения.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ Предварительно изучите теоретические основы работы №8. Механическим движением называется происходящее со временем перемещение тел или их частей относительно других тел (тел отсчета). Любое механическое движение рассматривается в определенной системе отсчета, состоящей из тела отсчета, связанной с ним системы пространственных координат и часов.
называют основным уравнением динамики. Эскиз машины Атвуда показан на рис.2. Два груза массами М соединены нитью, перекинутой через неподвижный блок. Если на один из грузов положить перегрузок массой m, то система приходит в ускоренное движение. Каждый из грузов натягивает участок нити, который, стараясь сократиться, действует на груз силой натяжения
а для другого груза:
Основное уравнение динамики вращательного движения неподвижного блока имеет вид:
где Если вращение по часовой стрелке считать положительным, то, согласно рис.2, получим
где R - радиус блока; Мтр - момент силы трения.
Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:
Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:
Наконец, в отсутствие скольжения нити по блоку ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока:
Проецируя уравнения (2) и (3) на ось У, направленную вертикально вверх, получим с учетом формул (5), (6) и (7) систему уравнений, к которой присоединим уравнение (4¢):
Умножая первое из уравнений (8) на -1 и складывая все уравнения (8), получим
В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство
Кроме того, в лабораторной установке величина момента инерции I блока такова, что справедливо другое неравенство:
Пренебрегая малыми величинами, из уравнения (9) получим ускорение а системы грузов под действием перегрузка массой m:
а модули сил натяжения нити Т1 и Т2 по обе стороны блока равны:
Можно сказать, что равенство (13) выполняется при двух предположениях (10) и (11). Равноускоренное движение системы грузов вдоль оси У описывается уравнениями движения произвольной точки системы:
где у1, v1 - начальные параметры. Исключая из этих уравнений время t при условии v1 = 0, получим
Система грузов перемещается на величину В точке с координатой у2 и скоростью v2 перегрузок подхватывается столиком и система грузов движется равномерно, перемещаясь на величину L2 за время t, измеряемое миллисекундомером экспериментальной установки. Подставляя в равенство (14) формулу
При изменении L2 меняется время t, измеряемое секундомером, но ускорение а должно оставаться неизменным. Уравнение (15) проверяется экспериментально в упражнении №1.
К основанию 1 экспериментальной установки (см.рис.3), которая стоит на регулируемых ножках 2, прикреплены миллисекундомер 3 и вертикальная стойка 4. К стойке крепятся три кронштейна, из которых два неподвижные - нижний 5 и верхний 6. А средний кронштейн 7 может перемещаться вдоль стойки. На кронштейне 7 находятся первый фотоэлектрический датчик 8 и столик 9 для снятия перегрузка. На нижнем кронштейне 5 установлен второй фотоэлектрический датчик 10 и резиновые амортизаторы 11. Все кронштейны содержат прорезь для определения положения кронштейна на вертикальной миллиметровой шкале 12. На верхнем конце стойки находится неподвижный блок 13. За блоком помещен электромагнит 14, при включении которого в сеть блок тормозится. И наоборот, при выключении тока нажатием кнопки "ПУСК" на передней панели установки система из грузов и перегрузка приходит в движение. Для наблюдения ускоренного движения грузов на правый груз 15 помещают перегрузок 16 и поднимают их в такое положение, в котором нижнее основание груза совпадает с чертой на верхнем кронштейне. После нажатия кнопки "ПУСК" начинается ускоренное движение грузов и перегрузка до того момента, когда столик 9 подхватит перегрузок. Одновременно фотоэлектрический датчик 8 включает миллисекундомер, измеряющий время равномерного движения грузов до тех пор, пока груз 15 не ударится об амортизатор II и не вызовет срабатывание датчика 10, выключающего миллисекундомер. Итак, во время равноускоренного движения грузы проходят расстояние L1 (см.рис.2) и приобретают скорость v2, с которой, двигаясь равномерно, проходят расстояние L2 за время t, измеренное миллисекундомером и показанное на табло "ВРЕМЯ, С". Для подготовки прибора к следующему измерению нажимают кнопку "СБРОС".
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Лабораторная работа №2 ИЗУЧЕНИЕ АБСОЛЮТНО НЕУПРУГОГО УДАРА
ЦЕЛЬ РАБОТЫ
Изучение абсолютно неупругого удара. Оценка действующих сил и величины необратимых потерь механической энергии при абсолютно неупругом ударе.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Материальной точкой называется тело, размеры которого много меньше масштаба движения. В дальнейшем в этом пункте под словом "тело" следует подразумевать материальную точку. Силы, действующие на тела механической системы, можно разделить на две группы: 1) внешние силы 2) внутренние силы
Система тел называется изолированной или замкнутой, если на тела системы не действуют внешние силы, т.е. Если ускорение
где Рассмотрим систему двух тел с массами m1 и m2. Пусть тела системы взаимодействуют с силами
Складывая уравнения (3) и (4) и учитывая равенство (1), получим
Из уравнения (5) следует закон сохранения импульса: если система является изолированной (
Изменение скорости
где Импульсами внешних сил, например, сил тяжести, а также перемещениями тел за малое время удара Dt можно пренебречь. В этом случае уравнения (3) и (4) принимают вид:
Складывая уравнения (3¢) и (4¢) с учетом (1), получим уравнение (6), т.е. при кратковременных взаимодействиях даже в неизолированных системах закон сохранения импульса приближенно выполняется. Удар называется абсолютно неупругим, если после удара скорости тел одинаковы:
Изменение кинетической энергии тел при абсолютно неупругом ударе равно
Для кратковременного удара изменениями положения тел и их потенциальной энергии Ер можно пренебречь: DЕр = 0. Так как DЕk < 0, то полная механическая энергия тел убывает, переходя в другие виды энергии. Удар, при котором полная механическая энергия тел сохраняется, называется абсолютно упругим. Закон сохранения механической энергии можно сформулировать так: полная механическая энергия системы тел сохраняется, если система изолирована и на тела системы не действуют внутренние диссипативные силы (например, силы трения).
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Упражнение 1. ОПРЕДЕЛЕНИЕ СРЕДНЕЙ СИЛЫ ТРЕНИЯ
1. Поместите гирю 5 (см.рис.4) на сравнительно небольшом расстоянии L1 от оси вращения О рычага 4. 2. Поднимите сваю 2 на максимальную высоту. 3. С помощью защелки 6 расположите груз 1 на такой высоте Н1, чтобы после удара с грузом свая не касалась втулки 3 своей горизонтальной платформой. 4. По вертикальной линейке 8 измерьте положение Н1 указателя груза и положение h1 указателя сваи до удара. Результаты измерения занесите в таблицу 1. 5. Нажимая на защелку 7, освободите груз. Наблюдайте абсолютно неупругий удар груза и сваи, а также их замедленное движение после удара. Измерьте положение h2 указателя сваи после удара и результат измерения запишите в таблицу 1. 6. Повторите пункты 2¸5 еще четыре раза при тех же значениях Н1 и h1. 7. Передвиньте гирю 5 вдоль рычага 4 на новое расстояние L2 от оси вращения О, установив гирю в середине рычага. Измените высоту Н1 поднятия груза. При изменении высоты Н1 поднятия груза необходимо контролировать выполнение пункта 3. Повторите измерения, указанные в пунктах 2 ¸ 6, при новом расстоянии L2. 8. Передвиньте гирю 5 на максимальное расстояние L3 от оси вращения О и повторите измерения, указанные в пунктах 2 ¸ 6.
9. Используя методику обработки результатов прямых измерений, изложенную в главе I, для каждого L найдите средние значения величин Н1, h1, h2 и полуширину доверительных интервалов DН1, Dh1, Dh2. 10. Для каждого L по формулам (14) и (15) найдите высоту Н падения груза и путь S замедленного движения тел после удара, а по формулам
определите полуширину доверительных интервалов этих величин. 11. Для каждого L по формуле (17) вычислите усредненную силу трения F, используя данные экспериментальной установки: m1 = 0,32 кг; m2 = 0,12 кг; Dm1 = Dm2 = Dm = 1 г = 0,001 кг. Пренебрегая погрешностью Dg ускорения свободного падения, полуширину доверительного интервала DF найдите по формуле:
Таблица 1
Результаты вычислений занесите в таблицу 1. Сравните силу трения F для разных значений L длины рычага, т.е. для разных величин силы нормального давления.
Упражнение 2. ОЦЕНКА ВЕЛИЧИНЫ 12. По формуле (11) оцените величину внутренней силы f, действующей на груз при абсолютно неупругом ударе груза и сваи, считая, что время удара Dt» 2×10-4 с. Сравните полученную силу с силой тяжести FТ = m1g, которая является внешней силой в системе "груз-свая".
Упражнение 3. ОПРЕДЕЛЕНИЕ НЕОБРАТИМЫХ ПОТЕРЬ
13. Подставляя формулу (8) в формулу (12), получим расчетную формулу для величины необратимых потерь механической энергии при абсолютно неупругом ударе груза и сваи:
Найдите величину необратимых потерь механической энергии dЕ, а полуширину доверительного интервала D(dЕ) этой величины определите с помощью формулы:
14. Долю g необратимых потерь механической энергии определите по формуле (13), а полуширину доверительного интервала Dg найдите с помощью формулы:
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Сформулируйте цель лабораторной работы 2. Сформулируйте закон сохранения импульса 3. Какой удар называется абсолютно упругим? 4. Какой удар называется абсолютно неупругим? 5. Что происходит с механической энергией при абсолютно неупругом ударе? 6. Выполняется ли закон сохранения импульса при кратковременном абсолютно неупругом ударе? 7. Какую скорость имеет груз после свободного падения с высоты Н = 1 м? 8. Какую скорость имел груз до удара о сваю, если после абсолютно неупругого удара скорость груза и сваи равна 2,4 м/с, а масса сваи в 3 раза меньше массы груза? 9. Выполняется ли закон сохранения механической энергии при свободном падении груза до удара? 10. Как движутся груз и свая после абсолютно неупругого удара? 11. Выполняется ли закон сохранения механической энергии при движении груза и сваи после удара?
12. Укажите формулу работы постоянной силы. 13. Как работа силы, действующей на тело, связана с изменением механической энергии тела? 14. Как найти силу, с которой свая действует на груз при их абсолютно неупругом ударе? 15. Каким должно быть соотношение между внешней силой F и внутренней f при кратковременном ударе, чтобы приближенно выполнялся закон сохранения импульса? 16. Чему равна величина необратимых потерь механической энергии при ударе груза и сваи? 17. Как меняется доля необратимых потерь механической энергии во время удара груза и сваи при увеличении массы сваи и неизменной массе груза? 18. Нарисуйте эскиз экспериментальной установки 19. Какая система тел является изолированной? 20. По какой формуле можно найти величину необратимых потерь механической энергии при ударе груза и сваи? 21. Как определяют высоту Н свободного падения груза до удара? 22. Как вычисляют полуширину доверительного интервала DН высоты свободного падения груза до удара? 23. Как определяют путь S замедленного движения груза и сваи после удара? 24. Как вычисляют полуширину доверительного интервала DS величины пути замедленного движения груза и сваи после удара? 25. По какой формуле определяют величину внешней силы F? 26. Как определяют полуширину доверительного интервала DF внешней силы? 27. Какая величина определяется в упражнении 2 и по какой формуле? 28. Как определяют полуширину доверительного интервала Df силы, с которой свая действует на груз? 29. Какая величина определяется в упражнении 3? 30. По какой формуле можно найти долю необратимых потерь механической энергии при ударе груза и сваи? Лабораторная работа №3
ЦЕЛЬ РАБОТЫ Определение коэффициента восстановления относительной скорости и необратимых потерь кинетической энергии при прямом центральном упругом ударе двух шаров.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Предварительно необходимо изучить теоретические основы работы № 2. Ударом твердых тел называется совокупность явлений, возникающих при столкновении движущихся твердых тел. Время удара t очень мало, составляет примерно
Линией удара MN называется общая нормаль к поверхностям соударяющихся тел в точке соприкосновения К (рис.6). Если центры масс С1 и С2 тел лежат на линии удара, то удар называется центральным, а если не лежат, то - нецентральным. Если скорости v1 и v2 центров масс тел в начале удара параллельны линии удара, то удар называется прямым, в противном случае - косым. Уравнения законов сохранения импульса и энергии, справедливых для абсолютно упругого удара, имеют вид:
где Решая эту систему для прямого центрального удара шаров, получим:
т.е. относительная скорость тел при абсолютно упругом прямом центральном ударе сохраняется по модулю, меняя свое направление на противоположное. При реальном прямом центральном ударе вместо уравнения (3) получим:
где k - коэффициент восстановления относительной скорости. При абсолютно упругом ударе k = 1; при абсолютно неупругом ударе k = 0; для упругих ударов реальных тел 1 > k > 0. В частности, при столкновении тел из дерева Решая совместно систему уравнений (1) и (4) для прямого центрального удара шаров, получим:
Отсюда легко определить величину необратимых потерь кинетической энергии при ударе:
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Упражнение 1. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВОССТАНОВЛЕНИЯ ОТНОСИТЕЛЬНОЙ СКОРОСТИ 1. С помощью винтов 8 (см.рис.7) отрегулируйте экспериментальную установку так, чтобы в положении равновесия шары касались друг друга, а их удар был прямым и центральным. Включите установку нажатием кнопки "СЕТЬ". 2. Найдите массы шаров m1 и m2 и запишите их в таблицу 1. 3. Измерьте штангенциркулем диаметры шаров d1 и d2 и линейкой длину нитей R1 и R2 от точек подвеса до поверхности шаров. 4. По формулам L1 = R1 + d1/2 и L2 = R2 + d2/2 найдите расстояния L1 и L2 от точек подвеса нитей до центров шаров. Если результаты вычислений отличаются друг от друга более чем на 1 мм, то подъемом или опусканием одного из шаров сравняйте длины L1 и L2. Тогда L1 = L2 = L. Результат измерения L запишите в таблицу. 5. Включите электромагнит нажатием кнопки ²ВКЛ². Поместите шар с меньшей массой m1 в гнездо электромагнита и измерьте угол g отклонения нити подвеса этого шара от вертикали. Убедившись в неподвижности другого шара, отпустите легкий шар нажатием кнопки ²ПУСК². Наблюдая прямой центральный удар шаров, измерьте и запишите в таблицу углы максимального отклонения a и b нитей подвеса шаров от вертикали после удара. Проведите наблюдения углов a, b, g не менее 5 раз. 6. Результаты измерения Таблица 1
7. Подставляя результаты измерения 8. Полуширину доверительного интервала Dk найдите по формуле:
где Da, Db, Dg - полуширины доверительных интервалов углов a, b, g, измеренные в радианах. 9. Результат измерения запишите в виде доверительного интервала: k ± Dk.
Упражнение 2. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ НЕОБРАТИМЫХ ПОТЕРЬ КИНЕТИЧЕСКОЙ ЭНЕРГИИ 10. Используя результаты измерения 11. Пренебрегая ошибками измерения длины подвеса шаров L, ускорения свободного падения g и масс шаров m1 и m2 , найдите полуширину доверительного интервала D(dЕ) по формуле:
Результат измерения запишите в виде: dЕ ± D(dЕ). 12. Оцените величину dЕ по формуле (15) и сравните с результатом, полученным в пункте 11.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте цель лабораторной работы. 2. Укажите явления, происходящие при упругом ударе твердых тел. 3. Оцените время удара твердых тел. 4. По какой формуле можно найти импульс ударной силы? 5. Сформулируйте законы сохранения импульса и механической энергии 6. Какой удар называется абсолютно упругим? 7. Какой удар называется абсолютно неупругим? 8. Сохраняется ли механическая энергия соударяющихся тел при реальном упругом ударе? 9. Какой удар тел называется центральным? 10. Какой удар называется: 1) прямым; 2) косым? 11. Какую величину называют коэффициентом восстановления относительной скорости? 12. Чему равен коэффициент восстановления относительной скорости при абсолютно упругом ударе твердых тел?
13. Укажите величину коэффициента восстановления относительной скорости тел при абсолютно неупругом ударе. 14. В каких пределах меняется величина коэффициента восстановления относительной скорости тел при реальном упругом ударе? 15. Напишите систему уравнений, решая которую можно найти скорости шаров после абсолютно упругого удара. 16. Какие скорости имеют шары равной массы после абсолютно упругого прямого центрального удара? 17. Какие уравнения образуют систему, решая которую можно найти скорости шаров после реального упругого удара? 18. Нарисуйте эскиз экспериментальной установки. 19. Какую величину определяют при выполнении упражнения 1? 20. Укажите порядок выполнения упражнения 1 21. По какой формуле получают значение угла в радианах? 22. Как высота подъема шара от положения равновесия связана с углом отклонения нити (стержня) подвеса от вертикали? 23. Как при выполнении данной работы находят скорости шаров до и после удара? 24. По какой формуле определяют коэффициент восстановления относительной скорости шаров, если после удара шары движутся в разные стороны? 25. По какой формуле вычисляют полуширину Dk доверительного интервала коэффициента восстановления относительной скорости шаров? 26. Какую величину определяют в упражнении 2? 27. Выполняется ли для кратковременного реального упругого удара закон сохранения импульса? 28. Укажите формулу для определения величины необратимых потерь кинетической энергии. 29. Укажите формулу для вычисления полуширины доверительного интервала величины необратимых потерь кинетической энергии. 30. Что происходит с механической энергией шаров при реальном упругом ударе?
Лабораторная работа № 4
Методом наклонного маятника
Цель работы Изучение закономерностей при внешнем трении и экспериментальное измерение коэффициента трения качения для различных материалов.
ТеоретическИе ОСНОВЫ РАБОТЫ Во всех механических явлениях имеют место силы трения, действие которых практически всегда связано с переходом механической энергии в тепловую. Силы всемирного тяготения, упругие силы, рассматриваемые в механике, а также силы взаимодействия электрически заряженных тел зависят только от конфигурации тел, то есть от их взаимного расположения, но не от их скоростей. Отличие сил трения от указанных сил состоит в том, что силы трения, помимо конфигурации, зависят от относительной скорости тех тел, между которыми они действуют. Силы трения могут возникать между соприкасающимися телами или их частями как при их относительном перемещении, так и при их относительном покое. Внешнее трение действует в плоскости касания двух прижатых друг к другу тел при их относительном движении (например, трение между бруском и наклонной плоскостью, с которой он соскальзывает). Внутреннее трение проявляется между различными частями одного и того же тела (между различными слоями жидкости или газа).
По кинематическому признаку внешнее трение можно разделить на трение скольжения и трение качения. Рассмотрим движение (качение) шара (или цилиндра) по горизонтальной поверхности и возникающее при этом движении трение качения. Для объяснения сил трения качения следует считать деформации шара (цилиндра) и плоскости качения неупругими, причем для простоты будем полагать, что деформируется только поверхность качения, и только она имеет некоторые пластические деформации (в реальных условиях возникают упругие и пластические деформации как шара (цилиндра), так и плоскости). Точка приложения и направление реакции опоры ( Уравнение проекций сил -mg +N·cosγ=0. (1) Угол γ практически мал, cosγ» 1, то есть N»mg. (2) Горизонтальная составляющая реакции опоры представляет собой силу трения качения Так как вращение шара (цилиндра) равномерное, и угловое ускорение его равно нулю, то должно выполняться условие равенства моментов* сил, то есть момент силы трения качения относительно точки С равен проекции силы нормального давления Ny, умноженной на К: Fтр·R=Nу·K, (3) где R - радиус шара (цилиндра); Nу = N×cosγ = N; К - линейная величина, называемая коэффициентом трения качения. Коэффициент трения качения имеет размерность длины, поэтому он называется также «плечом» силы трения качения шара (цилиндра). Из равенства (3) с учетом, что Nу»N получаем следующее выражение для силы трения качения:
В данной лабораторной работе предлагается один из способов исследования процесса трения качения - метод наклонного маятника. Шарик 1, подвешенный в точке О на нити длиной L, может катиться по наклонной плоскости 2, составляющей регулируемый угол α с горизонтальной поверхностью (рис.9а). ОО1 - направление (ось), фиксирующее положение равновесия наклонного маятника, точки А| и В| - проекции точек А и В на ось ОО1. Идея данного метода заключается в определении связи уменьшения угла φ отклонения нити маятника с коэффициентом трения качения К. Если маятник отклонить от положения равновесия на угол φ (точка А, рис.9а) и отпустить, то при отсутствии трения шарик 1 через половину периода* оказался бы в точке А1. Но при наличии трения качения шарик окажется (остановится) в точке В, нить маятника составит угол (φ-Dφ) с осью ОО1, причем точка В расположена ниже, чем точка А. Это означает, что происходит уменьшение потенциальной энергии маятника (DU), равное работе сил трения качения на пути АВ.
Следует отметить, что работой по преодолению сопротивления среды и трения в подвесе маятника ввиду их малости можно пренебречь. DU = Aтр, mgDh = FтрDS, (5) где m - масса шарика; Dh - потеря высоты (рис.9б); DS - длина дуги АВ; Fтр - сила трения качения, определяемая по формуле (4), в которой сила нормального давления тела (шара) на наклонной плоскости равна N = mg×cosα. (6) Из геометрических соображений определим Dh и DS. Длина дуги АВ равна (рис.9а) DS = L(2φ-Dφ), (7) где L - длина нити или радиус дуги АВ окружности. Изменение высоты Dh определяется как проекция отрезка A|B| на вертикальную ось (рис.9,б): Dh = (A|B|)×sina = DL×sina, где DL = A|B| = OB| - OA| = L×cos(j - Dj) - L×cosj, Dh = L×sina[cos(j - Dj) - cosj]. (8) Подставив в (5) формулы (4), (6), (7) и (8), получим следующее выражение: mg×L×sina[cos(j - Dj) - cosj] = (K×mg×cosa/R)×L(2j - Dj). (9) Учитывая, что Dj << 1 (за половину полного колебания потеря угла составляет порядка Dj @ 0,3° = 5,2×10-3 рад), то можно считать, что cosDj» 1, sinDj @ Dj и cos(j - Dj) = cosj×cosDj + sinj×sinDj = cosj + Dj×sinj. С у
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1036; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.130 (0.014 с.) |

 Материальной точкой называется тело, размеры которого много меньше масштаба движения. Положение материальной точки в пространстве характеризует ее радиус-вектор
Материальной точкой называется тело, размеры которого много меньше масштаба движения. Положение материальной точки в пространстве характеризует ее радиус-вектор  , проведенный из начала координат к этой точке. При движении материальной точки по траектории ее радиус-вектор меняется. Мерой изменения радиуса-вектора со временем является физическая величина - скорость
, проведенный из начала координат к этой точке. При движении материальной точки по траектории ее радиус-вектор меняется. Мерой изменения радиуса-вектора со временем является физическая величина - скорость  , а мерой изменения скорости со временем - ускорение
, а мерой изменения скорости со временем - ускорение  . Мерой действия одного тела на другое является физическая величина - сила
. Мерой действия одного тела на другое является физическая величина - сила  . Основные законы динамики материальных точек - это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого имеет вид:
. Основные законы динамики материальных точек - это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого имеет вид: , (1)
, (1) , а на блок - силой
, а на блок - силой  . Тогда на каждый груз действует сила тяжести
. Тогда на каждый груз действует сила тяжести 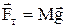 и сила натяжения нити
и сила натяжения нити  , (2)
, (2) . (3)
. (3) , (4)
, (4)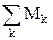 - алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I - момент инерции блока; e - угловое ускорение.
- алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I - момент инерции блока; e - угловое ускорение. , (4¢)
, (4¢) , т.е.
, т.е.  ;
;  . (5)
. (5)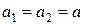 . (6)
. (6) или
или  . (7)
. (7) (8)
(8) . (9)
. (9) <<
<<  . (10)
. (10) <<
<<  . (11)
. (11) , (12)
, (12)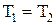 . (13)
. (13) ,
, ,
, . (14)
. (14) , двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12).
, двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12).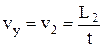 , получим
, получим . (15)
. (15) ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ , с которыми на тело с номером i действуют тела, не вошедшие в систему;
, с которыми на тело с номером i действуют тела, не вошедшие в систему; взаимодействия тел системы с номерами i и k. По третьему закону Ньютона:
взаимодействия тел системы с номерами i и k. По третьему закону Ньютона: или
или  . (1)
. (1) .
. записать в виде
записать в виде  ,
,  - малое изменение скорости тела за малый промежуток времени Dt, то второй закон Ньютона принимает вид
- малое изменение скорости тела за малый промежуток времени Dt, то второй закон Ньютона принимает вид или
или  , (2)
, (2) - начальная скорость тела;
- начальная скорость тела;  - конечная скорость спустя малый промежуток времени Dt. Величина
- конечная скорость спустя малый промежуток времени Dt. Величина  - импульс тела, а
- импульс тела, а  - импульс силы.
- импульс силы. и
и  и на тела действуют внешние силы
и на тела действуют внешние силы  и
и  . Запишем уравнение (2) для каждого тела системы:
. Запишем уравнение (2) для каждого тела системы: ; (3)
; (3) . (4)
. (4) . (5)
. (5) ;
;  ), то суммарный импульс тел такой системы сохраняется, т.е.
), то суммарный импульс тел такой системы сохраняется, т.е. . (6)
. (6) соударяющихся тел может быть достаточно большим, а время удара Dt очень мало (
соударяющихся тел может быть достаточно большим, а время удара Dt очень мало ( с). Поэтому ускорения тел и внутренние или ударные силы
с). Поэтому ускорения тел и внутренние или ударные силы  во время удара могут быть очень большими. Эти силы значительно превосходят внешние силы:
во время удара могут быть очень большими. Эти силы значительно превосходят внешние силы:  . Мерой механического воздействия на тело за время удара является импульс
. Мерой механического воздействия на тело за время удара является импульс  ударной силы
ударной силы  ,
, - средняя ударная сила за время Dt.
- средняя ударная сила за время Dt. ; (3¢)
; (3¢) . (4¢)
. (4¢)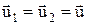 . Для такого удара уравнение (6) принимает вид
. Для такого удара уравнение (6) принимает вид .
. . (7)
. (7) ;
; 
 .
. . (18)
. (18) . (19)
. (19) . (20)
. (20) с. Процесс упругого столкновения двух тел можно разделить на две фазы. В первой фазе, которая начинается в момент соприкосновения тел, кинетическая энергия соударяющихся тел переходит в потенциальную энергию деформации. Первая фаза заканчивается прекращением сближения тел. Во второй фазе упругого удара тела расходятся, и потенциальная энергия упругой деформации тел переходит в их кинетическую энергию.
с. Процесс упругого столкновения двух тел можно разделить на две фазы. В первой фазе, которая начинается в момент соприкосновения тел, кинетическая энергия соударяющихся тел переходит в потенциальную энергию деформации. Первая фаза заканчивается прекращением сближения тел. Во второй фазе упругого удара тела расходятся, и потенциальная энергия упругой деформации тел переходит в их кинетическую энергию. Абсолютно упругим ударом называется такой удар, при котором сохраняется полная механическая энергия соударяющихся тел. При реальном упругом ударе часть механической энергии тел переходит в другие виды энергии (внутреннюю энергию, энергию звуковых волн и т.д.), т.е. появляется необратимая потеря механической энергии dЕ. Абсолютно неупругим ударом называется удар, после которого скорости тел одинаковы.
Абсолютно упругим ударом называется такой удар, при котором сохраняется полная механическая энергия соударяющихся тел. При реальном упругом ударе часть механической энергии тел переходит в другие виды энергии (внутреннюю энергию, энергию звуковых волн и т.д.), т.е. появляется необратимая потеря механической энергии dЕ. Абсолютно неупругим ударом называется удар, после которого скорости тел одинаковы.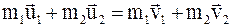 , (1)
, (1) , (2)
, (2) - скорости тел после удара.
- скорости тел после удара. , (3)
, (3) , (4)
, (4) , (5)
, (5) . (6)
. (6) . (7)
. (7) ,
,  ,
,  углов отклонения вычислите по формуле (1.1) главы I. Выборочные оценки S(
углов отклонения вычислите по формуле (1.1) главы I. Выборочные оценки S(
 ,
, . (16)
. (16) Трение между поверхностями двух соприкасающихся тел при отсутствии между ними жидкой, газообразной прослойки, называется сухим. Если между твердыми телами имеется тонкий слой жидкости (смазочного масла), то в этом случае трение называется жидкостным.
Трение между поверхностями двух соприкасающихся тел при отсутствии между ними жидкой, газообразной прослойки, называется сухим. Если между твердыми телами имеется тонкий слой жидкости (смазочного масла), то в этом случае трение называется жидкостным. ), или силы воздействия плоскости на катящийся шар (цилиндр) представлены на рис.8.
), или силы воздействия плоскости на катящийся шар (цилиндр) представлены на рис.8. и
и  .
. . (4)
. (4)



