
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основной закон теплопроводностиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Понятие теплопроводности охватывает собой процесс распространения тепла путем непосредственного соприкосновения между частицами тела. При этом в газах перенос энергии осуществляется путем диффузии молекул и атомов, а в жидкостях и твердых телах диэлектриках - путем упругих волн. В металлах перенос энергии, в основном, осуществляется путем диффузии свободных электронов, аfзии свободных электронов, и роль упругих колебаний кристаллической решетки здесь имеет второстепенное значение. Процесс распространения тепла вообще и процесс теплопроводности в частности неразрывно связан с распределением температуры. Поэтому прежде всего нам необходимо установить связанные с этим понятия температурного поля и температурного градиента. 1. Температурное поле. Температура, как известно, является параметром состояния тела и характеризует уровень внутренней энергии тела. В общем случае температура t является функцией координат х, у, zи времени τ, т. е. t = f(x, y, z,τ) (1) Совокупность значений температуры в данный момент времени для всех точек пространства называется темпера-турным полем. Уравнение (1) является математической фор-мулировкой температурного поля. При этом, если температура зависит от времени, то поле называется неустановившимся или нестационарным Температурное поле может быть функцией трех, двух и одной координаты. Соответственно оно называется трех-, двух- и одномерным. Наиболее простой вид имеет уравнение одно-
мерного стационарного температурного поля: t = f(x) (2) 2. Температурный градиент. Геометрическое место точек, имеющих одинаковую температуру, образует изотермическую поверхность. Так как в одной и той же точке пространства одновременно не может быть двух различных температур, то изотермические поверхности разных температур друг с другом не пересекаются. Все они или замыкаются на себя, или кончаются на границах тела. Изменение температуры в теле наблюдается лишь в направлениях, пересекающих изотермические поверхности (направление х рис.1). При этом наиболее резкое изменение получается в направлении нормали п к изотермическим поверхностям.
Рис. 1 К определению темпера- Рис. 2. Закон Фурье турного градиента
Предел отношения изменения температуры Δt к расстоя - нию между изотермами по нормали Δ п называется темпера-турным градиентом, который обозначается одним из следу-ющих символов:
Температурный градиент является вектором, направленным по нормали к изотермической поверхности. Его положительным направлением считается направление в сторону возрастания температуры. Значение температурного градиента, взятое с обратным знаком, называют падением температуры. 3. Тепловой поток. Тепловая энергия распространяется всегда только в сторону убывающей температуры. Количество теплоты Q в системе СИ определяется в Дж. Тепловым потоком называется количество теплоты Q, передаваемой в единицу времени , Дж/с = Вт (4) Плотностью теплового потока называется количество теплоты Q, проходящее в единицу времени через единицу поверхности , Дж/м2·с = Вт/м2 (5) Величина Q (а также q) является вектором, направление которого совпадает с направлением распространения тепла и противоположно направлению вектора температурного градиента (рис. 2). 4. Закон Фурье. Изучая явление теплопроводности в твердых телах, Фурье установил, что количество переданного тепла пропорционально градиенту температуры, времени и площади сечения, перпендикулярного направлению распространения тепла. , Дж (6а) Если количество переданного тепла отнести к единице времени, то установленную зависимость можно записать, так: , Вт (6в) Если количество переданного тепла отнести к единице времен и единице поверхности, то закон Фурье будет иметь вид , Вт/м2 (6с) Уравнение (6) является математическим выражением основного закона распространения тепла путем теплопроводности - закон Фурье. 5. Коэффициент теплопроводности. Коэффициент пропорциональности λ в уравнении (6) называется коэффициентом теплопроводности. Он является физическим параметром вещества и характеризует собой способность вещества проводить тепло: , Вт/м К (7) Следовательно, величина коэффициента теплопроводности определяет собой количество тепла, которое проходит в единицу времени через единицу поверхности при падении температуры в1° С на единицу длины.
Для различных веществ коэффициент теплопроводности различен и для каждого из них зависит от структуры, плотности, влажности, давления и температуры. Все вместе взятое сильно затрудняет выбор правильного значения коэффициента теплопроводности. При технических расчетах значения коэффициента теплопроводности обычно выбираются из справочных таблиц. При этом надо следить за тем, чтобы физические характеристики материала (структура, плотность, влажность, температура) были соответственны. Для ответственных расчетов значения коэффициента теплопроводности определять путем лабораторного изучения применяемого материала. Так как при распространении тепла температура в различных частях тела различна, то в первую очередь важно знать зависимость коэффициента теплопроводности от температуры. Как показал опыт, для подавляющего большинства материалов получается линейная зависимость, т. е. λ = λо (1+ bt), (8) где λо - значение коэффициента теплопроводности при 0°С и b - постоянная, определяемые опытным путем. В практических расчетах значение коэффициента теплопроводности обычно определяется по среднеарифметической из граничных значений температуры тела, и это значение принимается постоянным в рассматриваемом интервале температур.
Коэффициент теплопроводности газов лежит в пределах значений от λ = 0,005 до λ = 0,5 Вт/м К. С повышением температуры λ возрастает (рис.3), от давления практически не зависит, за исключением очень высоких (больше 2000 бар) и очень низких (меньше 20 мм рт. ст.) давлений. Коэффициент теплопроводности капельных жидкостей лежит в пределах от λ = 0,08 до λ = 0,6 Вт/м К. С повышением температуры для большинства жидкостей λ убывает (рис.4); исключение составляют лишь вода и глицерин. Для неассоциированных жидкостей (бензол, толуол, ксилол и другие углеводороды) значение коэффициента теплопроводности жидкостей можно определить по следующим формулам , (9) где , (10) где λ - коэффициент теплопроводности, Вт/м К; γ - плотность, кг/м3; теплоемкость, Дж/кг К; М - молекулярный вес; индексом о отмечены значения величин при 20 °С.
t оС Рис. 4 λ= f(t) различных капельных жидкостей 1- глицерин безводный; 2- муравьиная кислота; 3 – метиловый спирт; 4- этиловый спирт; 5 - касторовое масло; 6 - анилин; 7 - уксусная кислота; 8 - ацетон; 9 - бутиловый спирт; 10 - нитробензол; 11- изопропан, спирт; 12 - бензол; 13 - толуол; 14 - ксилол; 15 - вазелиновое масло.
Коэффициент теплопроводности огнеупорных и изоляционных материалов имеет значение в пределах от λ = 0,02 до λ = 2,5 Вт/мК.С повышением температуры он возрастает (рис.5). Как правило, для материалов с большим объемным весом коэффициент теплопроводности имеет более высокие значения. Он зависит также от структуры материала, его пористости и влажности. Для влажного материала коэффициент теплопроводности значительно выше, чем для сухого и воды в отдельности. Так, например, для сухого кирпича λ =0,3, для воды λ = 0,5, а для влажного кирпича λ = 0,9 Вт/м К. Это явление вызывает необходимость особого внимания как при определении коэффициента теплопроводности, так и при расчете теплопередачи.
оС Рис. 5. λ= f(t) различных изоляционных и огнеупорных материалов: 1- воздух; 2 - минеральная вата, γ =160 кг/м3; 3 - шлаковая вата, γ = 200 кг/м3; 4 - керамоволокнистый материал, γ = 130 кг/м3; 5 - покрытие из керамического волокна, γ = 160 кг/м3; 6- диатомовый кирпич, γ = 550 кг/м3; 7 - красный кирпич, γ = 1672 кг/м3; 8 - шлакобетонный кирпич, γ = 1373 кг/м3; 9 - шамотный кирпич, γ = 1840 кг/м3.
Коэффициент теплопроводности металлов лежит в пределах от λ = 2 до λ =360 Вт/м К. Самым теплопроводным металлом является серебро (λо = 360 Вт/м К), затем идут: красная медь (λо = 260 Вт/м К), алюминий (λо = 180 Вт/м К), железо (λо = 75,4 Вт/м К). Для большинства металлов с повышением температуры коэффициент теплопроводности убывает (табл.1). Особенность сталей состоит в том, что начиная с температур 800-1000 оС величина λ вновь возрастает. Величины теплопроводности сталей приведены в таблице 1 При наличии разного рода примесей коэффициент теплопроводности металлов резко убывает. Так, например, для чистой меди λ = 340 Вт/м К, для той же меди, но со следами мышьяка, λ = 122 Вт/м К. Таблица. 1 - Теплопроводность отожженных углеродистых сталей, Вт/м К.
Продолжение таблицы 1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.217.100 (0.011 с.) |

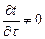 и имеет вид (1). Если же температура во времени не меняется, то поле называется установившимся или стационарным
и имеет вид (1). Если же температура во времени не меняется, то поле называется установившимся или стационарным 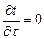 и имеет вид t = f(x, y, z).
и имеет вид t = f(x, y, z).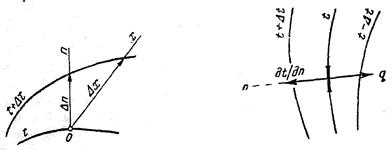
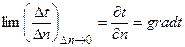 , К/м (3)
, К/м (3)


