Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эта сила сообщает электрону ускорение, определяемое II законом НьютонаСодержание книги
Поиск на нашем сайте
Кулоновская сила за время
При столкновениях с узлами кристаллической решетки электроны передают свою энергию проводнику, продолжая двигаться в вдоль проводника с некоторой небольшой по величине средней скоростью (скоростью дрейфа). Считаем, что после столкновения скорость электрона равна 0, а при равноускоренном движении равна среде арифметическому начальной и конечной скоростей:
Здесь Учитывая соотношение, определяющее среднюю скорость дрейфа электронов вдоль проводника, для силы и плотности тока получим
Если к концам проводника длиною
Таким образом, получили закон Ома для электрического тока. С учетом этого, для силы тока в проводнике получим
Из чего получаем закон Ома для участка цепи. Сопоставляя приведенное соотношение с полученным ранее законом Ома для участка цепи, можно придти к выводу о том, что проводник длиною
Эта формула полностью согласуется с формулой для сопротивления проводника, полученной ранее
Как видим, классическая электронная теория проводимости позволяет связать удельное сопротивление с индивидуальными свойствами проводника.
Из приведенной формулы следует, что чем меньше электронов в единице объема проводника, чем чаще они сталкиваются с узлами кристаллической решетки, тем больше их удельное сопротивление. Значит, причина электрического сопротивления металлов в столкновениях электронов с узлами кристаллической решетки, поэтому при протекании тока проводник нагревается. Наименьшим удельным сопротивлением обладают проводники, изготовленные из серебра. Далее следуют проводники из меди и алюминия. Численные значения удельного сопротивления для указанных металлов при 20оС приведены в таблице
Законы Ома и Джоуля-Ленца в дифференциальной и интегральной формах
Итак физическая модель электропроводимости — «идеальный электронный газ». Электрический ток - направленное движение свободных электронов в металле это «электронный идеальный газ». Для молекулы идеального газа справедливо соотношение:
на электрон находящийся в электрическом поле действует сила:
t - время движения электрона от соударения до соударения. Тогда:
Это закон Ома в дифференциальной форме, где
: Таким образом применяя для электронного газа в металлах модель идеального газа мы получили сугубо теоретически формулу экспериментального закона Ома, что является убедительным подтверждением правильности выбранной нами модели.
Аналогично
Закон Джоуля-Ленца:
предположим, что в момент удара вся кинетическая энергия электрона переходит в тепло, тогда при ударе n- электронов за время t количество выделившегося тепла определяется:
Совершенно просто такое представление об электронах как об “электронном газе” объясняет электросопротивление металлов: Электроны сталкиваясь с узлами электронной кристаллической решетки теряют свою скорость, а значит способность перемещаться и нагревают металл.
Проанализируем формулу:
E - заряд электрона m- масса электрона n- количество электронов (у всех металлов примерно одинакова) t - время от столкновения до столкновения (так как размеры кристаллической решетки мало различаются у разных металлов, то t у всех металлов примерно одинаково
У всех металлов близкая проводимость и мало того приблизительно одинаковая теплопроводность и отношение коэффициента теплопроводности к коэффициенту электропроводимости есть величина постоянная для всех металлов пропорционально абсолютной температуре
-закон Видемана и Франца.
К - коэффициент теплопроводности
Те металлы, которые лучше проводят электрический ток, лучше проводят тепло т.к. природа одинакова т.е. направленно движущиеся электроны. НО: «Электронный газ» никак не мог объяснить сверхпроводимость при низких температурах.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.216.107 (0.011 с.) |

 .
. между последовательными столкновения увеличит скорость электрона в направлении поля на величину
между последовательными столкновения увеличит скорость электрона в направлении поля на величину
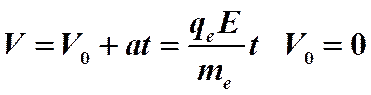 .
.
 .
. среднее время между двумя последовательными столкновениями.
среднее время между двумя последовательными столкновениями.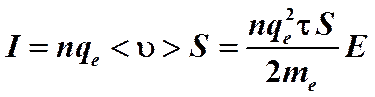 ,
, ,
,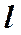 приложено напряжение
приложено напряжение  , то среднее значение напряженности электрического поля в проводнике будет равно
, то среднее значение напряженности электрического поля в проводнике будет равно .
. .
. обладает сопротивлением, величина которого определяется формулой
обладает сопротивлением, величина которого определяется формулой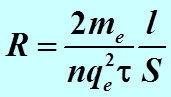 .,
., .,
., .
.  (5)
(5)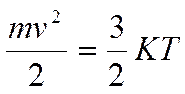


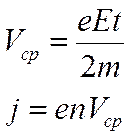
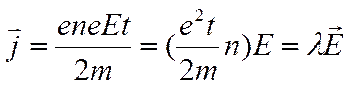
 - удельная проводимость
- удельная проводимость





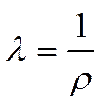



 ,
,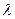 - коэффициент электропроводности
- коэффициент электропроводности