
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представим формулу (2) для плотности тока в видеСодержание книги
Поиск на нашем сайте
Приведенное соотношение называют законом Ома для участка цепи в дифференциальной форме. Величину
Тепловое действие тока Как отмечалось ранее, падение напряжения
Учитывая, далее, что при постоянном токе прошедший через проводник за время
для тепла
Формула (7) представляет закон Джоуля-Ленца и интегральной форме Работа силы за единицу времени называют мощностью. Поэтому мощность кулоновских сил или мощность электрического тока определится формулой
В СИ мощность измеряют в ваттах, а работу в джоулях. Поэтому
Работу тока измеряют также в кВт ч (киловатт-часах).
Подсчитаем количество тепла, выделяющееся за единицу времени в единице объема проводника. Пусть
Полученная формула (9) характеризует удельную тепловую мощность проводника и называется законом Джоуля-Ленца в дифференциальной форме.
Классическая электронная теория электропроводности металлов и ее опытные обоснования Металлы - проводники электрического тока. Строение металлов - кристаллическая решетка и свободные электроны. Атомы объединяясь в кристаллическую решетку обезличили большое количество электронов, тогда уместно применение ранее разработанной теории идеального газа.
Закон Джоуля-Ленца в дифференциальной и интегральной формах. Двигаясь под действием силы F = e E, электрон проводимости приобретает некоторую энергию
Провзаимодействовав с ионом кристаллической решетки, он отдает ему эту энергию, которая выделяется в проводнике в виде тепла. Если взаимодействие электрона проводимости с ионом кристаллической решетки происходило в течение времени t, то за это время в проводнике выделится в виде тепла энергия
где
Так как
то
где – время свободного пробега электрона проводимости.
Если в объеме проводника содержится n электронов проводимости, то энергия, переданная единице объема проводника в единицу времени всеми электронами,
Выражение (6.56) является математической формой записи закона Джоуля-Ленца в дифференциальной форме. Из формулы (6.56) можно получить формулу закона Джоуля Ленца в интегральной форме. Имеем
где g = 1/r;
E = U/dl,
dV = S dl.
Следовательно,
или
где
U = IR – напряжение.
Количество тепла, выделившееся в проводнике за время t,
Выражение (6.58) является математической формой записи закона Джоуля-Ленца в интегральной форме. В случае постоянного тока
Классическая электронная теория проводимости металлов смогла объяснить не только электропроводность металлов и сплавов, но и их теплопроводность, некоторые оптические свойства вещества, что является её крупным достижением. Однако с её помощью невозможно объяснить такие экспериментальные факты, как независимость теплоемкости металлов от наличия электронов проводимости и сверхпроводимости. Это связано с тем, что в ней электроны проводимости подчиняются законам идеального газа, законам статистики Максвелла-Больцмана. В действительности же для электронов проводимости справедлива квантовая статистика, и они подчиняются закону статистики Ферми-Дирака.
Сверхпроводимость. План: 10.1. Ограниченность классической электронной теории проводимости. 10.2. Открытие сверхпроводимости. 10.3. Особенности сверхпроводящего состояния вещества. 10.4. Высокотемпературная сверхпроводимость.
Ограниченность классической электронной теории проводимости. Открытие сверхпроводимости. Сопротивление некоторых металлов (Al, Pb, Zn и др.) и их сплавов при низких температурах T (0,14¸20 К), называемых критическими, характерных для каждого вещества, скачкообразно уменьшается до нуля, т.е. металл становится абсолютным проводником. Впервые это явление, называемое сверхпроводимостью, обнаружено в 1911 г. Г. Камерлинг-Оннесом для ртути. Было обнаружено, что при Т = 4,2 К ртуть, по-видимому, полностью теряет сопротивление электрическому току. Уменьшение сопротивления происходит очень резко в интервале нескольких сотых градуса. В дальнейшем потеря сопротивления наблюдалась и у других чистых веществ и у многих сплавов. Температуры перехода в сверхпроводящее состояние различны, но всегда очень низки.
Возбудив электрический ток в кольце из сверхпроводящего материала (например, с помощью электромагнитной индукции), можно наблюдать, что его сила в течение нескольких лет не уменьшается. Это позволяет найти верхний предел удельного сопротивления сверхпроводников (менее 10-25 Ом×м), что гораздо меньше, чем удельное сопротивление меди при низкой температуре (~10-12 Ом× м). Поэтому принимается, что электрическое сопротивление сверхпроводников равно нулю. Сопротивление до перехода в сверхпроводящее состояние бывает самым различным. Многие из сверхпроводников при комнатной температуре имеют довольно высокое сопротивление. Переход в сверхпроводящее состояние совершается всегда очень резко. У чистых монокристаллов он занимает интервал температур меньший, чем одна тысячная градуса. Сверхпроводимостью среди чистых веществ обладают алюминий, кадмий, цинк, индий, галлий. В процессе исследований оказалось, что структура кристаллической решетки, однородность и чистота материала оказывают значительное влияние на характер перехода в сверхпроводящее состояние. В 1914 г. К. Оннес обнаружил, что сверхпроводящее состояние разрушается магнитным полем, когда магнитная индукция B превосходит некоторое критическое значение. Критическое значение индукции зависит от материала сверхпроводника и температуры. Критическое поле, разрушающее сверхпроводимость, может быть создано и самим сверхпроводящим током. Поэтому имеется критическая сила тока, при которой сверхпроводимость разрушается. В 1933 г. Мейсснер и Оксенфельд обнаружили, что внутри сверхпроводящего тела полностью отсутствует магнитное поле. При охлаждении сверхпроводника, находящегося во внешнем постоянном магнитном поле, в момент перехода в сверхпроводящее состояние магнитное поле полностью вытесняется из его объема. Этим сверхпроводник отличается от идеального проводника, у которого при падении удельного сопротивления до нуля индукция магнитного поля в объеме должна сохраняться без изменения. Явление вытеснения магнитного поля из объема проводника называется эффектом Мейсснера. Эффект Мейсснера и отсутствие электрического сопротивления являются важнейшими свойствами сверхпроводника.
|
||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.49.32 (0.009 с.) |

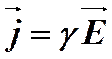 (6)
(6)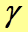 , обратную удельному сопротивлению проводника, называют удельной проводимостью. Она равна
, обратную удельному сопротивлению проводника, называют удельной проводимостью. Она равна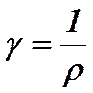
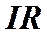 , связанное с силами сопротивления со стороны проводника, равно количеству тепла, выделяющемуся в проводнике при прохождению по нему 1 Кл электричества. Если по проводнику пройдет заряд
, связанное с силами сопротивления со стороны проводника, равно количеству тепла, выделяющемуся в проводнике при прохождению по нему 1 Кл электричества. Если по проводнику пройдет заряд 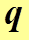 , то количество выделившегося в нем тепла будет равно
, то количество выделившегося в нем тепла будет равно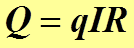 .
.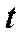 заряд
заряд  равен
равен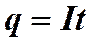 ,
,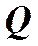 получим
получим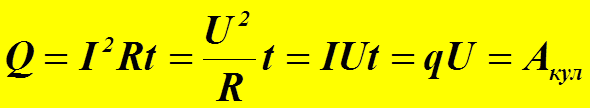 (7)
(7)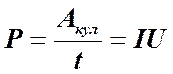 (8)
(8)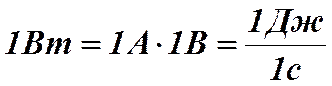
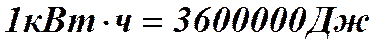 .
.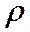 удельное сопротивление проводника,
удельное сопротивление проводника, 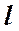 его длина,
его длина, 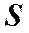 площадь поперечного сечения. Количества тепла, выделившееся в проводнике за
площадь поперечного сечения. Количества тепла, выделившееся в проводнике за 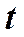 с, будет равно
с, будет равно
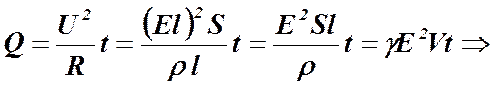
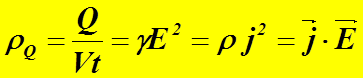 . (9)
. (9)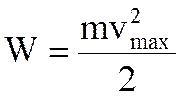 . (6.53)
. (6.53)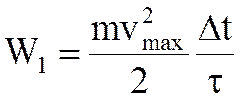 , (6.54)
, (6.54)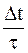 – число взаимодействий электрона проводимости с ионом кристаллической решетки.
– число взаимодействий электрона проводимости с ионом кристаллической решетки.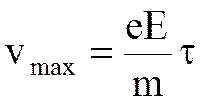
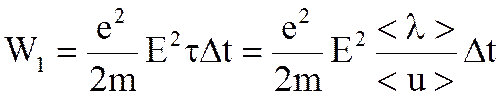 , (6.55)
, (6.55)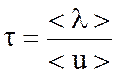
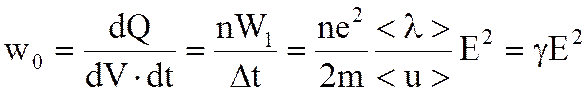 . (6.56)
. (6.56)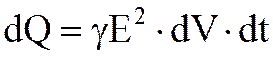 ,
,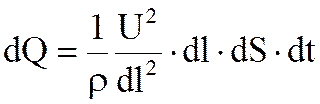
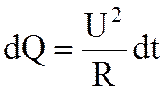 , (6.57)
, (6.57)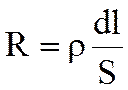 - сопротивление проводника;
- сопротивление проводника;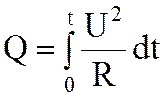 . (6.58)
. (6.58)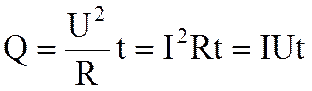 . (6.59)
. (6.59)


