
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Циркуляцией вектора напряженности магнитного поля по замкнутому контуру L (или просто циркуляцией вектора напряженности магнитного поля) называют интегралСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
С учетом того что напряженность магнитного поля от бесконечно длинного проводника с током
Таким образом,
Если ток протекает вне контура (рис. 2.2), то в этом случае можно записать
Соотношение
Теорема о циркуляциинапряженностимагнитного поля или законом полного тока в интегральной форме. Циркуляция вектора напряженности магнитного поля по замкнутому контуру L равна алгебраической сумме токов, охватываемых контуром, называется. Таким образом, из закона полного тока вытекают следующие следствия: а) если направление обхода контура и направление тока в проводнике не связаны между собой правилом правого винта, то значение
сохранив величину, изменит знак; б) если контур, расположенный в магнитном поле, не охватывает ток или алгебраическая сумма токов внутри замкнутого контура равна нулю, то
Зная связь между векторомнапряженности H и вектором индукции B магнитного поля, можно записать закон полного тока в интегральной форме для циркуляции вектора индукции:
Так как 2.2. Применение закона полного тока для расчета магнитных полей 2.2.1. Напряженность поля бесконечно длинного соленоида Соленоидом называют катушку цилиндрической формы из провода, витки которой намотаны в одном направлении и прилегают плотно друг к другу. Магнитное поле соленоида представляет собой результат сложения полей, создаваемых несколькими круговыми токами, расположенными рядом и имеющими общую ось (рис. 2.6). Внутри соленоида силовые линии каждого отдельного витка имеют одинаковое направление. Поэтому принято считать поле бесконечно длинного соленоида (такого, у которого диаметр гораздо меньше длины – d<<L) однородным, существующим только внутри его.
Рассчитаем напряженность магнитного поля внутри соленоида, длина которого L, радиус витка R, число витков N, сила тока I. Будем считать, что в любой точке соленоида вектор H направлен параллельно оси. Для расчета напряженности воспользуемся законом полного тока в виде
Выберем замкнутый контур прямоугольной формы (рис. 2.7), участок 1-2 которого расположен внутри соленоида вдоль его оси. Левую часть выражения (2.7) можно представить в виде
, где
Следовательно,
Правая часть выражения (2.16) может быть представлена так:
где n - число витков на единице длины соленоида;
I - величина тока в соленоиде. Таким образом, имеем
Откуда
Формула (2.8) согласуется с формулой, полученной с применением закона Био-Савара-Лапласа. Из полученного результата действительно видно, что напряженность магнитного поля внутри бесконечно длинного соленоида имеет одно и тоже значение, а следовательно, оно действительно однородно. Таким образом, действительно внутри бесконечно длинного соленоида напряженность магнитного поля практически везде одинакова. Она направлена вдоль оси соленоида в соответствии с правилом правого винта. Интегрируя по всем виткам, для индукции магнитного поля внутри соленоида окончательно получим
В случае бесконечно протяженного соленоида
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 2291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 .
. Окружность:
Окружность: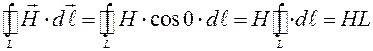 .
. , а
, а  , имеем
, имеем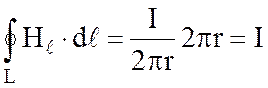 .
. . (2.2)
. (2.2)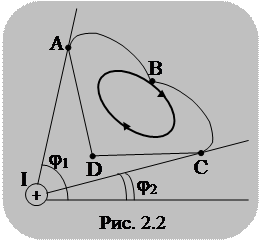 Если внутри замкнутого контура находятся n токов, то
Если внутри замкнутого контура находятся n токов, то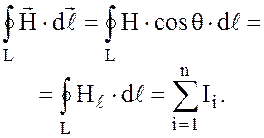 (2.3)
(2.3)
 (2.4)
(2.4) справедливо и в том случае, когда контур и проводник имеют произвольную форму. Если ток направлен «на нас», то вектор
справедливо и в том случае, когда контур и проводник имеют произвольную форму. Если ток направлен «на нас», то вектор  направлен «против часовой стрелки» (рис. 2.3). В этом случае
направлен «против часовой стрелки» (рис. 2.3). В этом случае  и
и  . В результате получим
. В результате получим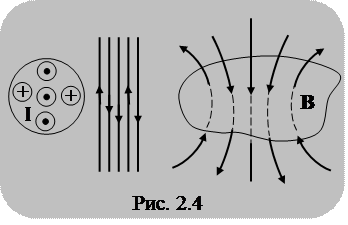 Если же контур охватывает
Если же контур охватывает  проводников с токами, направленными в разные стороны, то, учитывая, что от положения проводника внутри контура не зависит циркуляция
проводников с токами, направленными в разные стороны, то, учитывая, что от положения проводника внутри контура не зависит циркуляция  ,
, .
. . (2.6)
. (2.6) ,
,  , то магнитному полю нельзя приписать какой-либо потенциал, а это означает, что магнитное поле является вихревым, а не потенциальным.
, то магнитному полю нельзя приписать какой-либо потенциал, а это означает, что магнитное поле является вихревым, а не потенциальным.
 . (2.7)
. (2.7)

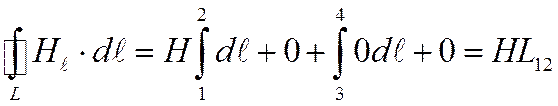
 , так как H перпендикулярен участку 2-3;
, так как H перпендикулярен участку 2-3;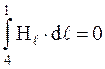 , так как H перпендикулярен участку 4-1;
, так как H перпендикулярен участку 4-1;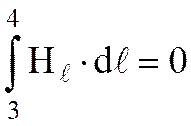 , так как участок 3-4 находится вне соленоида.
, так как участок 3-4 находится вне соленоида. .
.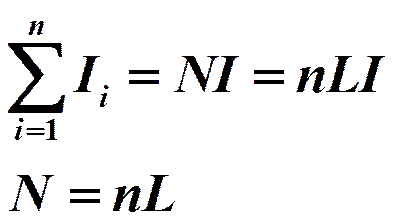 ,
,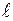 - длина участка;
- длина участка; .
. . (2.8)
. (2.8)
 .
. ,
,  . Поэтому индукция и напряженность магнитного поля внутри бесконечно протяженного соленоида будут равны
. Поэтому индукция и напряженность магнитного поля внутри бесконечно протяженного соленоида будут равны
 ,. (1)
,. (1)


