
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Градиент это производная от скалярной функции по направлению, в котором функция изменяется наибыстрейшим образом.Содержание книги
Поиск на нашем сайте
Градиент потенциала представляет собой вектор, направление которого совпадает с направлением наибыстрейшего возрастания потенциала. Знак «минус» указывает на то, что вектор напряженности электрического поля направлен в сторону убывания потенциала.
Эквипотенциальные поверхности. При перемещении заряда в направлении, перпендикулярном вектору напряженности электрического поля
Это значит, что траектория заряда принадлежит поверхности, точки которой имеют один и тот же потенциал. Такие поверхности называют эквипотенциальными поверхностями. Эквипотенциальные поверхности совместно с силовыми линиями используют для графического изображения электрических полей. Примеры графического изображения электрических полей представлены ниже:
Элементы теории поля. 1. Поток вектора
Циркуляция вектора.
Циркуляцией некоторого вектора  , вдоль замкнутого контура , вдоль замкнутого контура  ,называют криволинейный интеграл по контуру ,называют криволинейный интеграл по контуру  от скалярного произведения вектора от скалярного произведения вектора  дифференциал длины дуги контура дифференциал длины дуги контура 
-Т. Остроградского
-Т. Стокса
2)
2)
3)
4)
5)
6) 7)
Оператор Набла
Оператор Лапласа
div a =
ДИВЕРГЕНЦИЕЙ — (расхождение) вектора (а) называют предел отношения потока вектора (а) через замкнутую поверхность к величине объема, ограниченного этой поверхностью при условии, что объем стремится к нулю
“ ДИВЕРГЕНЦИЯ “ - это родник в лесу, а поток это количество воды прошедшее через поперечное течение русла реки
теорема Остаградского-Гауса или уравнение Максвелла
Этот закон можно представить в виде:
Приведенное соотношение часто называют теоремой Остроградского-Гаусса. Понятие потока вектора является одним из фундаментальных понятий электродинамики. Рассмотрим его более подробно. Выделим в электрическом поле небольшую плоскую площадку площадью
Поэтому поток вектора
Поток вектора
Покажем справедливость теоремы Остроградского-Гаусса на примере электрического поля, созданного точечным зарядом. В силу сферической симметрии электрического поля вектор
Точно такое же значение для напряженности поля точечного заряда было получено ранее с помощью закона Кулона.
Циркуляцией некоторого вектора
Используя понятие циркуляции вектора, независимость работы консервативных сил от вида траектории можно представить в виде утверждения о том, что циркуляция вектора консервативной силы на замкнутой траектории равна нулю. В силу того, что напряженность электрического поля равна консервативной силе, действующей на единичный положительный заряд, для циркуляции вектора электрической напряженности
Из приведенного соотношения следует, что циркуляция вектора электрической напряженности Данное утверждение будет справедливо тогда, когда отсутствуют магнитные поля. В присутствие магнитных полей циркуляция вектора
Приведенное соотношение представляет собой известный закон Фарадея об электромагнитной индукции, в соответствие с которым ЭДС, наведенная в замкнутом контуре, равна скорости изменения магнитного потока, пронизывающего этот контур. Два других закона электродинамики касаются свойств магнитного поля и его связи с электрическим полем. Один из них утверждает, что поток вектора магнитной индукции
Приведенное соотношение указывает на то, что в природе не существуют магнитные заряды. Источником магнитного поля являются движущиеся электрические заряды – электрический ток. В отличие от силовых линий электрического поля, которые начинаются на положительных зарядах и заканчиваются на отрицательных зарядах, силовые линии магнитного поля являются замкнутыми линиями, Они нигде не начинаются и нигде не заканчиваются. Поэтому говорят, что магнитное поле в отличие потенциального электрического поля является соленоидальным полем.
Примеры расчета электрических полей простейших систем электрических зарядов. ПРИМЕНЕНИЕ ТЕОРЕМЫ ОСТРОГРАДСКОГО-ГАУССА ДЛЯ РАСЧЕТА ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ
1. Равномерно заряженная плоскость 2.

Ф = 2 Ф (1) + 4 Ф (2) = 2 E S + 4 Eфсos90 ` = 2ES
2. Две равномерно заряженные плоскости.
3. Равномерно заряженный бесконечный цилиндр.
Ф = Ф бок + 2 Ф осн = E Sбок cos 0` + 2 E (1) S осн cos90`= E 2 ПrL +0
E
r
4. Равномерно заряженный шар
Если сфера радиусом Или
По поводу термина электростатического смещения:
 Электрическое смещение - физическая величина численно равная величине заряда “сместившегося “ изнутри проводника к поверхности на единицу поверхности. Электрическое смещение - физическая величина численно равная величине заряда “сместившегося “ изнутри проводника к поверхности на единицу поверхности.
Поток вектора
Очевидно, что поток
где
Принимая во внимание, что величина
Из полученной формулы следует, что электрическое поле, бесконечно протяженной равномерно заряженной плоскости является однородным. На любом расстоянии от плоскости вектор напряженности
Чтобы найти потенциал в каждой точки поля, воспользуемся соотношением, связывающим его с напряженностью поля
Если ось
Интегрируя последнее выражение, для разности потенциалов между точками электрического поля бесконечно протяженной равномерно заряженной плоскости получим
Из приведенной формулы следует, что эквипотенциальные поверхности параллельны заряженной плоскости, и что разность потенциалов между эквипотенциальными поверхностями растет линейно с расстоянием между ними.
Представим графически структуру электрического поля бесконечно протяженной равномерно заряженной плоскости, несущей положительный и отрицательный за
ряды Аналогичную структуру имеет гравитационное поле Земли вблизи ее поверхности. Вектором напряженности гравитационного поля являетсяускорение свободного падения
Используя теорему Остроградского – Гаусса, легко показать, что электрическое поле равномерно заряженной сферы за пределами сферы будет иметь вид
Величина напряженности электрического поля вблизи поверхности сферы может быть представлена соотношением
где Используя теорему Остроградского-Гаусса, подсчитаем напряженность и потенциал электрического поля, созданного бесконечно протяженной равномерно заряженной нитью. Очевидно, что силовые линии электрического поля перпендикулярны нити. Поэтому в качестве поверхности удобно выбрать цилиндрическую поверхность сосную с нитью. Поток вектора
Принимая во внимание, что величина
Для получения формулы для разности потенциалов в электрическом поле нити, заметим, что
Интегрируя приведенное выражение, для разности потенциалов получим
Разность потенциалов называют напряжением. В Международной системе единиц - СИ потенциал и разность потенциалов (напряжение) измеряют в вольтах:
С учетом этого ранее приведенные формулы для разности потенциалов между двумя эквипотенциальными поверхностями можно представить в виде: 1. В однородном электрическом поле напряжение
Поэтому напряженность электрического поля измеряют также в 2. В сферически симметричном поле:
3. В поле с цилиндрической симметрией (бесконечно протяженной заряженной нити):
Принимая во внимание формулу для работы электрических сил
введем новую единицу для работы и энергии. Это электрон-вольт – 1эВ=1,6 10-19Дж. 1эВ равен работе поля по перемещению электрического заряда, равного заряду электрона, между точками поля с разностью потенциалов 1 В.
2.1.2. Лекция 2. Электростатика. Электрическое поле в вакууме. План: 2.1. Электризация тел. Законы сохранения электрического заряда и Кулона. 2.2. Основные характеристики электрического поля: напряженность и потенциал. 2.3. Принцип суперпозиции электрических полей. 2.4. Напряженность электрического поля как градиент его потенциала. 2.5. Работа электрического поля по перемещению электрического заряда.
2.1. Электризация тел. Законы сохранения электрического заряда и Кулона.
Электрический заряд - физическая величина, характеризующая свойство тел или частиц вступать в электромагнитные взаимодействия и определяющая значения сил и энергий при таких взаимодействиях. Электрические заряды делятся на положительные и отрицательные. Закон сохранения электрического заряда - физический закон, в соответствии с которым в замкнутой системе взаимодействующих тел алгебраическая сумма электрических зарядов (полный электрический заряд) остается неизменной при всех взаимодействиях. Закон сохранения заряда гласит, что алгебраическая сумма зарядов электрически замкнутой системы, сохраняется. q1+q2+q3+…qn = const Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу. В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако, такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. То есть был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме. Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность можно записать в математической форме:
Здесь Ω — некоторая произвольная область в трёхмерном пространстве, Переходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса можно переписать закон сохранения заряда в локальной дифференциальной форме
Закон Кулона - основной закон электростатики, выражающий зависимость силы взаимодействия двух неподвижных точечных зарядов от расстояния между ними. Два неподвижных точечных заряда взаимодействуют с силой прямо пропорциональной произведению величин этих зарядов и обратно пропорциональной квадрату расстояния между ними и диэлектрической проницаемости среды, в которой находятся заряды. Важно отметить, что для того, чтобы закон был верен необходимы: 3. точечность зарядов — то есть расстояние между заряженными телами много больше их размеров. 4. их неподвижность. Иначе уже надо учитывать возникающее магнитное поле движущегося заряда. В векторном виде закон записывается следующим образом:
где e0 = 8,85×10-12 Ф/м – электрическая постоянная; q1, q2 – величины взаимодействующих зарядов; r1,2 – расстояние между зарядами; r0 – единичный вектор, показывающий направление силы.
2.2. Основные характеристики электрического поля: напряженность и потенциал. Для количественной характеристики электрического поля вводится в рассмотрение физическая величина, называемая напряженностью электрического поля. Напряженность электрического поля – векторная физическая величина. Она численно равна силе, действующей на положительный единичный заряд, помещенный в данную точку поля. Если электрическое поле создается точечным зарядом q, то согласно определению напряженность такого поля
Напряженность электрического поля является его силовой характеристикой. Направление вектора E совпадает с направлением силы, действующей на заряд, помещенный в данную точку поля. Он направлен по радиальной прямой, проходящей через заряд и рассматриваемую точку поля от заряда, если он положительный, и к заряду, если он отрицательный (рис. 1.2). За единицу напряженности электрического поля принимается напряженность в такой точке, в которой на заряд, равный единице, действует сила, равная единице. В системе СИ напряженность электрического поля измеряется в Кл/м или В/м. Электростатический потенциал — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля. Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда. Напряжённость электростатического поля Е и потенциал φ связаны соотношением:
В СИ за единицу разности потенциалов принимают вольт (В). Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в один кулон нужно совершить работу в один джоуль.
2.3. Принцип суперпозиции электрических полей. Если электрическое поле создано системой точечных зарядов: q1, q2, q3,........., то в произвольной точке пространства "А" каждый из них порождает свое собственное поле с соответствующей напряженностью: E1, E2, E3,.......... Результирующее поле в этом случае будет характеризоваться результирующим вектором напряженности электрического поля:
Величину и направление результирующего вектора напряженности E можно определить правилами геометрического сложения. Таким образом, для электрических полей оказывается справедливым принцип суперпозиции.
2.4. Напряженность электрического поля как градиент его потенциала. Градиент - вектор равный сумме произведений частных производных некоторой скалярной функции U=j()по переменным на их единичные векторы.в направлении быстрейшего изменения х,у,z некоторого скаляра, характеризующий быстроту этого изменения. Напряженность электростатического поля равна градиенту его потенциала: E= - gradφ.
В однородном электрическом поле:
- единица измерения напряженности электрического поля.
2.5. Работа электрического поля по перемещению электрического заряда. Если в электростатическом поле точечного заряда q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд qo, то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении dl равна
где dr = dl×cosa. Работа при перемещении заряда q из точки 1 в точку 2
где k – коэффициент пропорциональности, зависящий от выбора системы единиц измерения физических величин. В системе СИ k = 1/4pe0; q1 – заряд, создающий электрическое поле; q2 – заряд, перемещаемый в электрическом поле; r1, r2 – начальное и конечное расстояния между зарядами. Из формулы видно, что работа сил электрического поля по перемещению электрического заряда не зависит от траектории перемещения, а определяется только начальным и конечным положением зарядов. Следовательно, электростатическое поле электрических зарядов является потенциальным, а электростатические силы – консервативными силами.
Плотность заряда:

поверхностная обьемная
X
Y
d Ф (AA`BB`) = E (x,y,z) dxdy cos 180 = - E (x,y,z) dxdy d Ф (DD`CC`) = E (x+dx,y,z)dxdy cos0 = E (x+dx,y,z) dxdy
d Ф (1-2) = E (x,y,z + d Ф (3-4) = d Ф (5-6) = dФ = ( div a =
ДИВЕРГЕНЦИЕЙ — (расхождение) вектора (а) называют предел отношения потока вектора (а) через замкнутую поверхность к величине объема ограниченного зтой поверхностью при условии, что объем стремится к нулю
“ ДИВЕРГЕНЦИЯ “ - это родник в лесу, а поток это количество воды прошедшее через поперечное течение русла реки
теорема Остаградского-Гауса или уравнение Максвелла
Часть III Электрическое поле в среде. Диполь. Различают полярные и неполярные диэлектрики. Дипольный момент
в котором Примеры: H2O, NH3, SO2, CO. В неполярных молекулах в отсутствие электрического поля центры положительных и отрицательных зарядов совпадают. N2, H2, O2, CO2, CH4, но
при внесении неполярной молекулы в однородное электрическое поле центры зарядов смещаются. Молекула поляризуется и в результате приобретает дипольный момент. Этот момент пропорционален величине напряженности этого поля.
Силы создают вращающий момент:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 481; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.211.246 (0.013 с.) |

 работа не совершается
работа не совершается
 .
.





 .
.













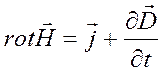















 :
:  :
: 

 - оператор Набла
- оператор Набла



 . (I)
. (I) . Поток вектора
. Поток вектора  через выделенную площадку
через выделенную площадку  будет равен скалярному произведению векторов
будет равен скалярному произведению векторов  и
и  . Площадку представляют вектором
. Площадку представляют вектором 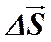 , величина которого равна площади площадки, а направление совпадает с направлением единичного вектора нормали
, величина которого равна площади площадки, а направление совпадает с направлением единичного вектора нормали  к этой площадке. Другими словами
к этой площадке. Другими словами 
 через площадку
через площадку  будет равен
будет равен .
. через произвольную замкнутую поверхность будет равен сумме или интегралу элементарных потоков
через произвольную замкнутую поверхность будет равен сумме или интегралу элементарных потоков .
.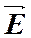 в любой точке сферы будет перпендикулярен поверхности сферы и иметь одну и ту же величину. Поэтому поток через выделенную сферическую поверхность, в центре которой находится заряд, будет равен
в любой точке сферы будет перпендикулярен поверхности сферы и иметь одну и ту же величину. Поэтому поток через выделенную сферическую поверхность, в центре которой находится заряд, будет равен .
. Из полученного соотношение следует, что величина напряженности электрического поля точечного заряда на расстоянии
Из полученного соотношение следует, что величина напряженности электрического поля точечного заряда на расстоянии  от него, будет равна
от него, будет равна

 Чтобы сформулировать другой фундаментальный закон электродинамики введем в рассмотрение новое математическое понятие - понятие о циркуляции вектора.
Чтобы сформулировать другой фундаментальный закон электродинамики введем в рассмотрение новое математическое понятие - понятие о циркуляции вектора. вдоль элементарного участка произвольной кривой называют интеграл от скалярного произведения вектора
вдоль элементарного участка произвольной кривой называют интеграл от скалярного произведения вектора  на элементарное перемещение
на элементарное перемещение  или
или  .
. будет справедливо соотношение
будет справедливо соотношение .
. на замкнутом контуре не равна нулю. Она определяется скоростью изменения магнитного потока, пронизывающего данный контур. Это утверждение представляет собой содержание одного из фундаментальных законов электродинамики. Его записывают в виде
на замкнутом контуре не равна нулю. Она определяется скоростью изменения магнитного потока, пронизывающего данный контур. Это утверждение представляет собой содержание одного из фундаментальных законов электродинамики. Его записывают в виде . (II)
. (II) через любую замкнутую поверхность равен нулю:
через любую замкнутую поверхность равен нулю: .
.




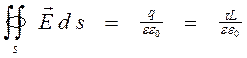




 R
R




 центрально симметрично окружает шар, то
центрально симметрично окружает шар, то 


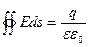


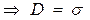
 Проведем оценку структуры электрического поля бесконечно протяженной, однородно заряженной плоскости. Для расчета напряженности электрического поля заметим, что силовые линии электрического поля от бесконечно протяженной плоскости будут перпендикулярны этой плоскости. Чтобы воспользоваться теоремой Остроградского-Гаусса (I-м законом электродинамики) выделим на плоскости площадку DS и построим на ней замкнутую цилиндрическую поверхность, образующие которой параллельны линиям вектора
Проведем оценку структуры электрического поля бесконечно протяженной, однородно заряженной плоскости. Для расчета напряженности электрического поля заметим, что силовые линии электрического поля от бесконечно протяженной плоскости будут перпендикулярны этой плоскости. Чтобы воспользоваться теоремой Остроградского-Гаусса (I-м законом электродинамики) выделим на плоскости площадку DS и построим на ней замкнутую цилиндрическую поверхность, образующие которой параллельны линиям вектора  . Поток вектора
. Поток вектора 
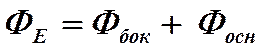 .
. вектора
вектора  вектора
вектора  ,
, напряженность поля, например, в точке
напряженность поля, например, в точке  , принадлежащей основанию цилиндра. Теперь из теоремы Остроградского-Гаусса для напряженности получим
, принадлежащей основанию цилиндра. Теперь из теоремы Остроградского-Гаусса для напряженности получим .
. характеризует поверхностную плотность заряда, для напряженности электрического поля равномерно заряженной бесконечно протяженной плоскости получим следующую формулу
характеризует поверхностную плотность заряда, для напряженности электрического поля равномерно заряженной бесконечно протяженной плоскости получим следующую формулу

 направить вдоль вектора напряженности поля
направить вдоль вектора напряженности поля  .
.
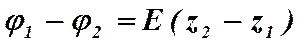 .
.

 , как сила, действующая на единичную массу. Потенциалом гравитационного поля является величина, определяемая потенциальной энергией единичной массы
, как сила, действующая на единичную массу. Потенциалом гравитационного поля является величина, определяемая потенциальной энергией единичной массы .
. Если заряд сферы распределен равномерно по ее поверхности, то напряженность электрического поля внутри сферы будет равна нулю, а потенциал точек внутри сферы будет одинаковым, равным потенциалу ее поверхности. Если радиус сферы равен
Если заряд сферы распределен равномерно по ее поверхности, то напряженность электрического поля внутри сферы будет равна нулю, а потенциал точек внутри сферы будет одинаковым, равным потенциалу ее поверхности. Если радиус сферы равен 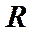 , то ее потенциал определится формулой
, то ее потенциал определится формулой
 ,
, - поверхностная плотность заряда, распределенного по поверхности сферы.
- поверхностная плотность заряда, распределенного по поверхности сферы.
 характеризует линейную плотность заряда, для напряженности электрического поля бесконечно протяженной равномерно заряженной нити получим следующую формулу
характеризует линейную плотность заряда, для напряженности электрического поля бесконечно протяженной равномерно заряженной нити получим следующую формулу .
.
 .
. .
. .
.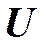 и напряженность
и напряженность  связаны между собой соотношениями:
связаны между собой соотношениями: .
. .
. .
. ,
,  .
. ,
,
 — граница этой области, ρ — плотность заряда,
— граница этой области, ρ — плотность заряда, 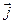 — плотность тока (плотность потока электрического заряда) через границу.
— плотность тока (плотность потока электрического заряда) через границу.


 . (1.3)
. (1.3)

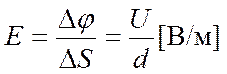
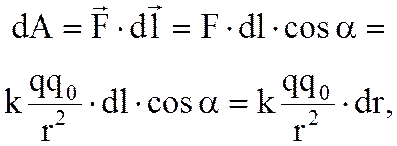

 ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА.
ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА.


 :
: 


 Z
Z 

 dxdydz
dxdydz dxdydz
dxdydz dxdydz
dxdydz


 определяется соотношением
определяется соотношением
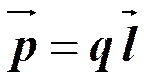 ,
, - величина одного из зарядов,
- величина одного из зарядов,  - расстояние между ними. Вектор
- расстояние между ними. Вектор  направлен от отрицательного к положительному заряду.
направлен от отрицательного к положительному заряду.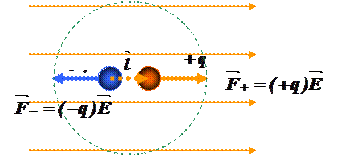

 .
. или
или  ,
,


