
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряженность магнитного поля тороидаСодержание книги
Поиск на нашем сайте
Магнитное поле тороида (тороид – это соленоид, свитый в кольцо) однородное, сосредоточено внутри самого тороида. Вне тороида поле отсутствует. Линиивектора H представляют собой концентрические окружности, центры которых совпадают с центром тороида. Краевой эффект у тороида (такого соленоида) отсутствует
где R - радиус тороида (радиус линии вектора H, расположенной в средней части тороида). Имеем
Откуда
Так как в нашем случае R = r, то
Внутри тороида напряженность магнитного поля имеет различные направления, поэтому говорить о его однородности можно только условно, т.е.
Магнитный момент
Поместим прямоугольную рамку с током в однородное магнитное поле и рассчитаем силы, действующие на нее со стороны поля. На верхнюю и нижнюю стороны рамки длиною  действуют равные по величине силы действуют равные по величине силы  и и  , которые создают вращающий момент величиной , которые создают вращающий момент величиной
В приведенной формуле Введем в рассмотрение новую векторную величину
И называемую магнитным моментом. Как следует из формулы (2), магнитный момент численно равен произведению площади «витка» (рамки) на величину тока в нем. Его направление совпадает с направлением нормали к плоскости «витка». Это направление связано с направлением тока правилом «правой руки». Учитывая это, формулу (1) для вращающего момента магнитных сил можно представить в более компактном виде
Из формулы (3) следует, что вращающий момент магнитных сил
Следует заметить, что магнитные силы Поэтому результирующее действие магнитных сил определяется вращающим моментом
Взаимная связь направлений тока и магнитного момента представлена на рисунке. Величина магнитного момента рамки равна
Легко видеть, что направление магнитного момента  совпадает с направлением магнитной индукции совпадает с направлением магнитной индукции 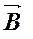 в центре «витка» с током. в центре «витка» с током.
С направлением вектора магнитной индукции связывают понятие о магнитных полюсах. Плоскость витка, из которой выходит вектор Поток и циркуляция вектора магнитной индукции Особенности магнитного поля определяются приведенными ниже уравнениями Максвелла
Из уравнения следует, что поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. Это указывает на то, что магнитные заряды в природе не существуют. Из уравнения (IV) следует, что источником магнитного поля являются либо движущиеся заряды (электрический ток) либо изменяющееся электрическое поле. Силовые линии магнитного поля, в чем мы убедились, изучая магнитное поле проводника с током, являются замкнутыми кривыми. Поэтому в отличие от электрического потенциального поля магнитное поле является вихревым или соленоидальным полем. Покажем, что полученный ранее результат о величине индукции магнитного поля бесконечно протяженного проводника с током в полной мере согласуется с уравнением (IV), из которого следует, что циркуляция вектора магнитной индукции по замкнутому контуру равна току, охватываемому этим контуром. Для контура в виде окружности радиуса
Особенно просто выглядит уравнение (или теорема) о циркуляции, если вместо вектора магнитной индукции
Покажем, как с помощью уравнения о циркуляции можно рассчитать величину магнитного поля внутри бесконечно протяженного соленоида, по которому течет ток величиной
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1684; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.118.151 (0.006 с.) |

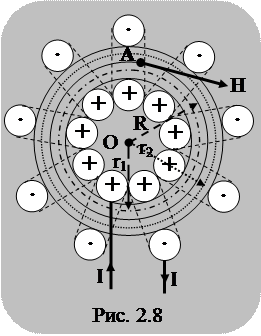 Выбирая одну из линий вектора H за контур обхода, радиус которого r (r1, r2), и применяя закон полного тока, будем иметь
Выбирая одну из линий вектора H за контур обхода, радиус которого r (r1, r2), и применяя закон полного тока, будем иметь ;
;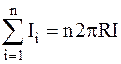 ,
, .
.
 . (2.9)
. (2.9) . (2.10)
. (2.10) .
.

 . (1)
. (1) длина боковой стороны рамки,
длина боковой стороны рамки, 
 угол между единичным вектором нормали и вектором магнитной индукции поля,
угол между единичным вектором нормали и вектором магнитной индукции поля,  площадь рамки
площадь рамки , определяемую соотношением
, определяемую соотношением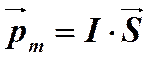 (2)
(2) . (3)
. (3) равен векторному произведению магнитного момента
равен векторному произведению магнитного момента  на вектор магнитной индукции
на вектор магнитной индукции  . Формула (3) справедлива для любой формы витка, находящегося в однородном магнитном поле. В случае неоднородного магнитного поля она будет справедлива для витка малых размеров. Формулу (3) часто используют для определения магнитной индукции как величины, определяемой отношением максимального вращающего момента магнитных сил к величине магнитного момента.
. Формула (3) справедлива для любой формы витка, находящегося в однородном магнитном поле. В случае неоднородного магнитного поля она будет справедлива для витка малых размеров. Формулу (3) часто используют для определения магнитной индукции как величины, определяемой отношением максимального вращающего момента магнитных сил к величине магнитного момента. .
.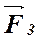 и
и  не создают моментов. Они деформируют (растягивают) рамку.
не создают моментов. Они деформируют (растягивают) рамку. и
и  , который рассчитывается по формуле
, который рассчитывается по формуле .
.
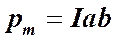 .
.
 или вектор
или вектор  , называют северным магнитным полюсом. При этом противоположная плоскость витка, в которую входит вектор
, называют северным магнитным полюсом. При этом противоположная плоскость витка, в которую входит вектор  .
. .
.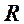 , центр которой находится на проводнике, циркуляция вектора
, центр которой находится на проводнике, циркуляция вектора  , касательного к этой окружности, будет равна
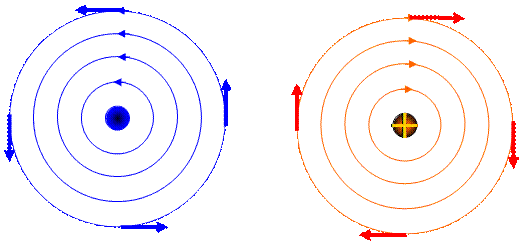
, касательного к этой окружности, будет равна .
.
 использовать сонаправленный с ним вектор напряженности магнитного поля
использовать сонаправленный с ним вектор напряженности магнитного поля  . Как известно
. Как известно .
. . Прежде заметим, что соленоид это навитый на цилиндрическую поверхность проводник, по которому течет ток. Соленоид характеризуют числом витков
. Прежде заметим, что соленоид это навитый на цилиндрическую поверхность проводник, по которому течет ток. Соленоид характеризуют числом витков  и длиной
и длиной  . Очевидно, что соленоид представляет собой
. Очевидно, что соленоид представляет собой 


