
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
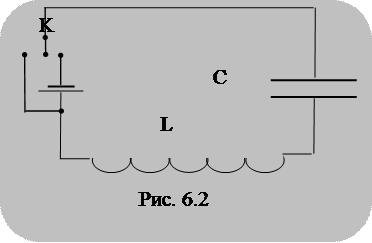
В цепи, содержащей индуктивность и емкость, могут возникать электрические колебания. Поэтому такая цепь называется к о л е б а т е л ь н ы м к о н т у р о м.Содержание книги
Поиск на нашем сайте
Колебания в контуре можно вызвать либо сообщив обкладкам конденсатора некоторый начальный заряд, либо возбудив в индуктивности ток (например, путем выключения внешнего магнитного поля, пронизывающего витки катушки). Присоединим отключенный от индуктивности конденсатор к источнику напряжения. Это приведет к возникновению на обкладках разноименных зарядов. Между обкладками возникает электрическое поле, энергия которого Растающая энергия магнитного поля.
Колебательные
Сосредоточенными
Активное сопротивление контура равно нулю, полная энергия не расходуется на нагревание проводов и будет оставаться постоянной. Поэтому, когда напряжение на конденсаторе = 0, энергия магнитного поля и ток достигают наибольшего значения. Дальше ток уменьшается, когда заряды на обкладках достигнут первоначального значения, сила тока станет равной нулю. Затем те же процессы протекают в обратном направлении, после чего система приходит в исходное состояние и весь цикл повторяется. В ходе процесса периодически изменяются заряд на обкладках, напряжение на конденсаторе и сила тока, текущего через индуктивность. Колебания сопровождаются взаимными превращениями энергии магнитного и электрического полей.
Уравнение свободных колебаний имеет вид: Переливание магнитной энергии катушки в электрическую энергию конденсатора аналогичны переливанию кинетической энергии грузика в потенциальную энергию пружины. Математическую модель можно получить из второго правила Кирхгофа. Всякий реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постоянно расходуется в этом сопротивлении на нагревание, вследствие чего свободные колебания затухают.
– линейное дифференцированное уравнение второго порядка с постоянными коэффициентами. Его решение определяется соотношением коэффициентов:
1)
β – коэффициент затухания
Затухание колебаний принято характеризовать логарифмическим декрементом затухания. Здесь a(t) – амплитуда соответствующей величины (q, U или I). Логарифмический декремент обратен числу колебаний, совершаемых за время, в течение которого амплитуда уменьшается в е раз.
r = 0 - свободные колебания
2)
А это означает, что колебаний в контуре не будет.
Апериодическое движение
Критическое сопротивление!
2)
N – число колебаний, за которое амплитуда уменьшится в е раз. R ≠ 0 – затухающие колебания
R < RK
– относительная полуширина резонансной кривой. Колебательный контур часто характеризуют его добротностью, которая определяется как величина, обратно пропорциональная логарифмическому декременту затухания. Добротность контура тем выше, чем большее число колебаний успевает совершиться прежде, чем амплитуда уменьшится в е раз. Величина обратная относительной полуширине резонансной кривой называется добротностью контура.
Q – является характеристикой "избирательного воздействия внешней вынуждающей периодической эдс с чистотой ω на колебательный контур. Добротность
Добротность прямо пропорциональна числу колебаний, за которое амплитуда уменьшится в е раз. ФИЗИЧЕСКИЙ СМЫСЛ ДОБРОТНОСТИ
I0max
ω1 ωp ω2 ω
ПОДДЕРЖАНИЕ КОЛЕБАНИЙ Широкий промежуток (контур)
D – дроссель – малое сопротивление для постоянного тока, и большое – для переменной 2) автоколебательная система (поющая дуга)
D b
0 I0 I
t
I
U подталкивает ток
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ Чтобы вызвать вынужденные колебания, нужно оказывать на систему внешнее периодически изменяющееся воздействие. В случае электрических колебаний это можно осуществить, если включить последователь с элементами контура переменную ЭДС или, разорвав контур, подать на разорвавшиеся контакты переменное напряжение. Это напряжение можно прибавить к ЭДС самоиндукции. U = Um cos ω2t = εвн
неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами и специальной правой частью. Его общее решение получится если к общему решению однородного уравнения:
прибавить частное решение неоднородного:
Где
Анализ: 1) – гармонические колебания происходящие с частотой w= 2) - амплитуда вынужденных колебаний зависит от Um амплитуды внешней ЭДС. 3) амплитуда вынужденных колебаний зависит от параметров колебательной системы wo и b, 4)!!!!! а также от соотношение частот вынуждающей силы w и собственной частоты wo
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.106.211 (0.008 с.) |

 . Если затем отключить источник напряжения и замкнуть конденсатор на индуктивность, емкость начнет разряжаться и в контуре потечет ток. В результате энергия электрического поля будет уменьшаться, но возникнет воз
. Если затем отключить источник напряжения и замкнуть конденсатор на индуктивность, емкость начнет разряжаться и в контуре потечет ток. В результате энергия электрического поля будет уменьшаться, но возникнет воз



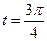






 системы с
системы с параметрами
параметрами
 - формула Томсона.
- формула Томсона.


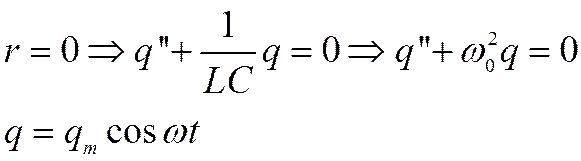



 - сопротивление контура мало!!!
- сопротивление контура мало!!!


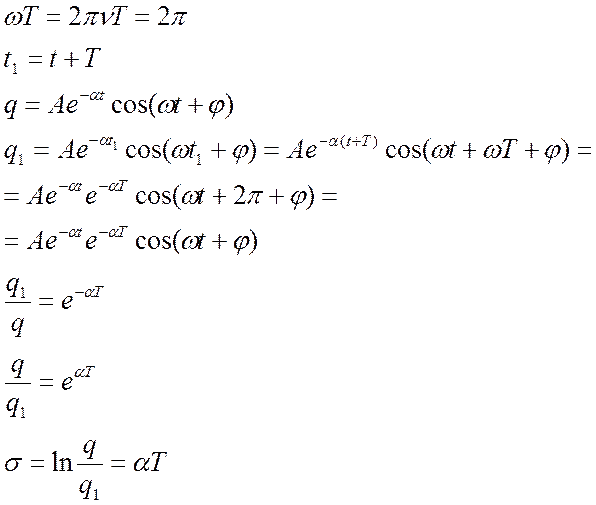

 Сопротивление контура велико!
Сопротивление контура велико! – мнимое число!
– мнимое число!
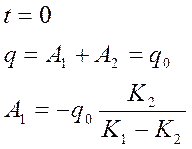



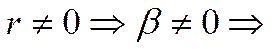 решение зависит от соотношения коэффициентов.
решение зависит от соотношения коэффициентов.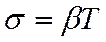 – логарифмический декремент затухания
– логарифмический декремент затухания

 – коэффициент затухания
– коэффициент затухания


 R > RK
R > RK




 I0
I0

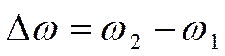 – полуширина резонансной кривой
– полуширина резонансной кривой




 i
i






 ε
ε 


 0
0
 – D
– D колебания не замыкаются на источник тока, а происходят в контуре.
колебания не замыкаются на источник тока, а происходят в контуре.


 + D a
+ D a


 ε
ε 



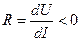 –падающая вольт-амперная характеристика сопротивления.
–падающая вольт-амперная характеристика сопротивления. U
U

 U1
U1
 U0
U0
 U2
U2


 I1 I2
I1 I2
 I I' = I0 + I – суммарный ток в контуре
I I' = I0 + I – суммарный ток в контуре I0 t
I0 t
 t
t
 U U' = U0 + U
U U' = U0 + U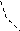
 напряжение
напряжение


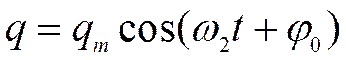


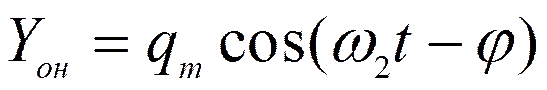 ,
,


 равной частоте внешней ЭДС.
равной частоте внешней ЭДС.



