
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прежде подсчитаем индукцию магнитного поля в центре кругового тока и в точках на перпендикуляре к плоскости витка, проходящего через его центр.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В центре витка индукция и напряженность магнитного поля будут равны
Индукция и напряженность магнитного поля на перпендикуляре к центру витка определятся соотношениями
Используя полученные результаты, рассчитаем индукцию и напряженность магнитного поле в центре бесконечно протяженного соленоида, в витках которого течет ток  . Индукция от выделенной части соленоида . Индукция от выделенной части соленоида
Как следует из чертежа
Принимая во внимание приведенные соотношения, далее получим
Интегрируя по всем виткам, для индукции магнитного поля внутри соленоида окончательно получим
В случае бесконечно протяженного соленоида
В приведенных формулах величина Формулы (1) можно получить, используя уравнение Максвелла (IV) о циркуляции вектора магнитной индукции. Для этого выберем замкнутую кривую, которая проходит внутри соленоида, выходит из него под прямым углом, проходит вне соленоида и аналогичным образом под прямым углом к оси соленоида возвращается в соленоид у другого конца.
Циркуляция вектора  по выбранному контуру будет равна по выбранному контуру будет равна
где
Магнитное поле в веществе. Магнетики.
В 1907 г. Резерфорд предложил планетарную модель атома.
!!!!!! Магнитные свойства вещества связаны с микротоками электронов !!!!!
Вращающийся по орбите электрон создает микроток величиной
Орбитальный магнитный момент электрона Намагничение естественно характеризовать магнитным моментом единицы объема. Эту величину называют намагниченностью и обозначают
Вектор намагниченности – магнитный момент единицы объема вещества.
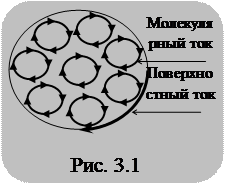
Вектор намагниченности J – векторная физическая величина, характеризующая магнитные свойства вещества и равная суммарному магнитному моменту единицы объема магнетика. Аналог поляризуемости диэлектрика. Возникающие в магнетике микротоки можно условно представить (заменить) как поверхностный ток. А он создает магнитное поле. Опять изумительная аналогия с поверхностными зарядами в диэлектрике. J – линейная плотность поверхностного тока в магнетике I = jl P = IS = jlS = jV
Вектор намагниченности численно равно линейной плотности поверхностных токов. Для диэлектриков вектор поляризации равен поверхностной плотности связанных зарядов.
Напряженность и индукция магнитного поля внутри магнетика. В обычном состоянии элементарные токи ориентированны в пространстве произвольным образом, поэтому Р=0. В случае внесения магнетика в магнитное поле он намагничивается и внешнее магнитное поле внутри магнетика изменяется. Результирующее магнитное поле равно:
- индукция, создаваемая внешним полем
- индукция, создаваемая поверхностными токами
Где J – намагниченность. Она зависит от внешнего магнитного поля. Если магнетик изотропный, то H↑↓J или H↑↑J B = μ0(H ± J) Для анизотропных направлений B и H не совпадают. Для изотропных магнетиков
χ – магнитная восприимчивость
где μ – относительная магнитная проницаемость или просто магнитная проницаемость вещества, χ – характерная для данного магнетика величина, называемая магнитной восприимчивостью. В отличие от диэлектрической восприимчивости, которая может иметь лишь положительные значения, магнитная восприимчивость может быть как положительной, так и отрицательной. Поэтому магнитная проницаемость может быть как больше, так и меньше единицы.
Классификация магнетиков В зависимости от того, как магнетик изменяет внешнее магнитное поле они разделяются на диа-, пара-, и ферромагнетики. Классификационным признаком является магнитная проницаемость среды μ μ < 1 –(χ меньше 0), т.е.магнитное поле ослабляется, т.е вектора J, H (коллинеарны и) направлены в противоположные стороны.
Если μ>1, то вектора J, H сонаправлены и магнитное поле усиливается в парамагнетике.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 581; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.85.123 (0.011 с.) |


 .
.

 .
.
 .
. ,
, 
 .
. .
. .
. ,
, . Поэтому индукция и напряженность магнитного поля внутри бесконечно протяженного соленоида будут равны
. Поэтому индукция и напряженность магнитного поля внутри бесконечно протяженного соленоида будут равны
 ,. (1)
,. (1) определяется числом витков на единице длины соленоида.
определяется числом витков на единице длины соленоида.
 , (2)
, (2) длина соленоида. Циркуляция
длина соленоида. Циркуляция 
 .
.


 . А его магнитный момент Р равен
. А его магнитный момент Р равен -
- .
.




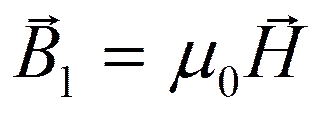

 ,
,
 ,
,


