
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение плотности тока и напряженности магнитного поля внутри проводникаСодержание книги
Поиск на нашем сайте
Для цилиндрического проводника плотность тока определяется по формуле:
где Напряжённость магнитного поля равна:
Бесселевы функции J0(qr) и J1(qr) от комплексного аргумента
тоже являются комплексами и могут быть представлены в показательной форме:
где b0-модуль, а β0—аргумент функции J0(qr); b1-модуль, а β1—аргумент функции J1(qr). Таблица 2.1. Модули и аргументы функций J0(qr) и J1(qr)
Аргументами β0 и β1 пренебрегаем и не используем в вычислениях, т.к. графики строятся по значению модуля функции Бесселя. Т.е. запишем это в виде:
mа=m×m0= 90 ×4p×10-7 = 1130,4 ×10-6 Гн/м;
При r = 0 (В центре проводника).
При r = 0,2R = 0,48 мм.
Выполним аналогичные расчеты для точек, находящихся на расстоянии от оси провода r = 0,3 R; r = 0,5 R; r = 0,7 R; r = 0,9 R; r = 1.0 R и запишем результаты в таблицу: Таблица 2.2. Результаты расчетов при f = 300 Гц
Определим плотность тока и напряженность магнитного поля внутри проводника при f1=nf=14∙300=4200 Гц.
mа=m×m0= 90 ×4p×10-7 = 1130,4 ×10-6 Гн/м;
Выполним аналогичные расчеты для точек, находящихся на расстоянии от оси провода r=0,3; R r=0,5R; r=0,7R; r=0,9R;r=R и запишем результаты в таблицу: Таблица 2.3. Результаты расчетов при f =4200 Гц
Построение графиков зависимости модуля плотности тока и напряженности магнитного поля от расстояния от центра провода
Рис.2.2.График зависимости модуля плотности тока от r
Рис.2.3.График зависимости напряженности магнитного поля от r Распределения напряженности магнитного поля снаружи проводника. Напряжённость магнитного поля снаружи проводника равна:
Осуществим расчеты в точках, находящихся на расстоянии от оси проводника соответственно r = 1R; r = 1,2 R; r = 1,5 R; r = 2R; r = 5 R; r = 10 R; r = 15 R; r = 25 R; r = 50 R.
Рис. 2.4. Напряженность магнитного поля снаружи проводника Определение величины потока вектора Пойнтинга (на единицу длины) внутри проводника с электрическим током Поток вектора Пойнтинга равен
Рис.2.5. Направление вектора Пойнтинга
Распределение энергии магнитного поля снаружи проводника Для определения энергии магнитного поля снаружи проводника будем использовать формулу:
где
Откуда
Осуществим расчеты в точках, находящихся на расстоянии от оси проводника соответственно r = 1R; r = 1,2 R; r = 1,5 R; r = 2R; r = 5 R; r = 10 R; r = 15 R; r = 25 R; r = 50 R и построим по ним соответствующий график.
Рис. 2.6. Распределение энергии магнитного поля снаружи проводника
Выводы: 1. Плотность тока и напряженность внутри проводника возрастают по мере увеличения r. Чем больше частота, тем медленнее возрастают плотность тока и напряженность. 2. Напряженность магнитного поля снаружи проводника убывает с увеличением расстояния от оси проводника. 3. Вектор Пойтинга направлен к центру проводника и равен 0,1207 ВА/м2. 4. Энергия магнитного поля снаружи проводника убывает с увеличением r. Расчет параметров металлического магнитного экрана 1. Рассчитать оптимальные линейные размеры и вес магнитного экрана цилиндрической формы (рис.3.1), расположенного в однородном магнитном поле напряженности 42,5 А/м2, который должен обеспечивать заданный коэффициент экранирования (материал – сталь ШХ-15). Определить величину напряженности магнитного поля во внутренней области магнитного экрана. Величину относительной магнитной проницаемости брать в соответствии с напряженностью магнитного поля Но. 2. Исследовать зависимость коэффициента экранирования магнитного экрана от напряженности внешнего магнитного поля, который изменяется в указанном диапазоне напряженности магнитного поля Но (приложение Б). 3. Рассчитать параметры магнитного экрана, имеющего минимальные габаритные размеры и вес.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 ,
, .
.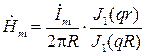 .
.

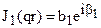 ,
, Рис. 2.1. Функции Бесселя нулевого и первого порядка
Рис. 2.1. Функции Бесселя нулевого и первого порядка
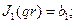

 рад/с;
рад/с;
 - на поверхности проводника.
- на поверхности проводника.
 ;
;  ;
;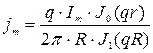 =
=  =207996,83 А/м2
=207996,83 А/м2 =0 А/м
=0 А/м

 =228796,5 А/м2
=228796,5 А/м2 =40,18 А/м
=40,18 А/м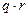


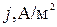

 рад/с;
рад/с;
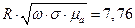 - на поверхности проводника.
- на поверхности проводника.


 .
.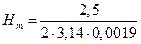 =209,52 А/м при r = 1R;
=209,52 А/м при r = 1R; =174,6 А/м при r = 1,2 R;
=174,6 А/м при r = 1,2 R; =138,225 А/м при r = 1,5 R;
=138,225 А/м при r = 1,5 R; =104,76 А/м при r = 2R;
=104,76 А/м при r = 2R; =41,9 А/м при r = 5 R;
=41,9 А/м при r = 5 R; =20,95 А/м при r = 10 R
=20,95 А/м при r = 10 R =13,96 А/м при r = 15 R
=13,96 А/м при r = 15 R =8,38 А/м при r = 25 R
=8,38 А/м при r = 25 R =4,19 А/м при r = 50 R
=4,19 А/м при r = 50 R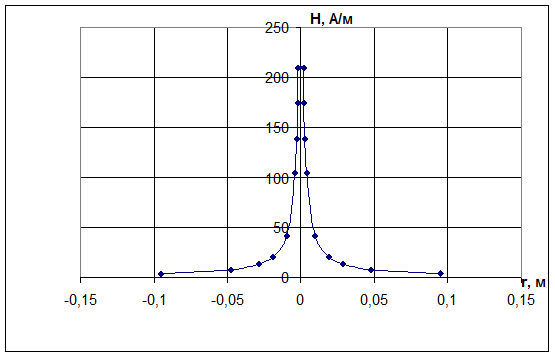
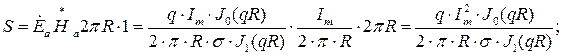
 =0,1207 ВА/м2.
=0,1207 ВА/м2.
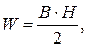
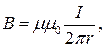
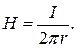
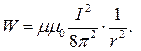

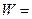 77,8 Вт/м2 при r = 1R
77,8 Вт/м2 при r = 1R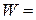 19,4 Вт/м2 при r = 2R
19,4 Вт/м2 при r = 2R



