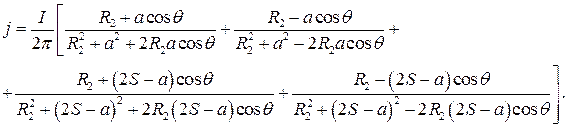Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет проводимости системы на единицу длины. Ток утечки.Содержание книги
Поиск на нашем сайте
Заменим кабель системой четырех линейных токов так, чтобы оболочка кабеля была эквипотенциальной поверхностью. Для этого должны выполнятся условия:
где r+ и r- расстояния от точки наблюдения до положительного и отрицательного проводов соответственно. Тогда, учитывая аналогию электростатических и стационарных полей и выбрав φ=0 в точке (0;0), получим:
где b = S − a.
Проводимость симметричной пары на единицу длины:
Подставив данные, получим: G0 = 11,174∙10-4 См/м. Тогда ток утечки: I0 = G0∙U = 0,2458 А/м. Построение графиков распределения напряжённости электрического поля и потенциала в плоскости KF Уравнение для потенциала в любой точке пространства:
С определяется из начальных условий, что φ(x,y) = 0 при x = 0, y = 0 → С = 0 В плоскости KF (как и на оси ОХ) y = 0, поэтому уравнение для потенциала перепишется так:
Рисунок 1.2. График распределения потенциала электрического поля
Закон распределения напряженности:
при y = 0:
Рисунок 1.3. График распределения напряженности электрического поля в плоскости KF
3. Распределения энергии электрического поля системы проводников вдоль оси Y Для определения энергии электрического поля снаружи проводника воспользуемся формулой:
где
Откуда
Рисунок 1.4 Распределение энергии электрического поля системы проводников вдоль оси Y 4. Построение эквипотенциали с потенциалом, равным 0,28 U Система симметрична относительно оси ОХ, следовательно координата Y цент-ра окружности эквипотенциали равна 0. 0,28 U = 61,6 В;
Корни уравнения: x1 = -10,121 мм; x2 = -11,839мм; Центр эквипотенциали:
Радиус эквипотенциали: r = (11,839 – 10,121)/2= 0,859 мм.
Рисунок 1.5. Изображение эквипотенциали
5. Рассчитать и построить график распределения плотности тока по цилиндрической поверхности проводника с радиусом R2.
Рисунок 1.6 Схема из двух проводников
Плотность тока определяется по формуле:
где
или
Рис.1.7 Распределение плотности тока по цилиндрической поверхности Выводы: - потенциал внутри маленьких проводников с радиусами R1 постоянен и для левого и правого проводников одинаков; - напряженность поля внутри проводников с радиусами R1 равна нулю; - энергия электрического поля системы проводников вдоль оси Y распределена неравномерно; - эквипотенциаль есть окружность с центром в точске (-0,010998;0) и радиуса 0,859 мм, находящаяся в маленьком левом проводнике R1; - плотность тока по цилиндрической поверхности распределена неравномерно. Расчет магнитного поля проводника с электрическим током. По круглому цилиндрическому проводнику протекает синусоидальный электрический ток i = 2,5 sin wt. Радиус проводника равен 1,9мм, удельная электропроводность металла равна s=5,6МСм/м, относительная магнитная проницаемость металла равна m=90. 1. Определить распределение плотности электрического тока и напряженности магнитного поля внутри проводника (расчеты осуществить в точках, находящихся на расстоянии от оси проводника, соответственно r = 0; r = 0,2 R; r = 0,3 R; r = 0,5 R; r = 0,7 R; r = 0,9 R; r = 1.0 R при двух частотах электрического тока: 300 и 4200). 2. Построить графики зависимостей модулей плотности электрического тока и напряженности магнитного поля внутри проводника от расстояния r. 3. Определить распределение напряженности магнитного поля снаружи проводника (расчеты осуществить в точках, находящихся на расстоянии от оси проводника соответственно r = 1.0 R; r = 1,2 R; r = 1,5 R; r = 2R; r = 5 R; r = 10 R; r = 15 R; r = 25 R; r = 50 R). Построить график распределения. 4. Определить величину потока вектора Пойнтинга (на единицу длины) внутри проводника с электрическим током. На чертеже указать направление вектора Пойнтинга. 5. Рассчитать и построить график распределения энергии магнитного поля снаружи проводника (расчеты осуществить в точках, указанных в п.3).
|
||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.110.145 (0.006 с.) |


 Можно сказать, что получена система из двух двухпроводных линий. Известно, что потенциал поля двухпроводной линии выражается в электростатике через линейную плотность зарядов:
Можно сказать, что получена система из двух двухпроводных линий. Известно, что потенциал поля двухпроводной линии выражается в электростатике через линейную плотность зарядов: ,
,
 .
.

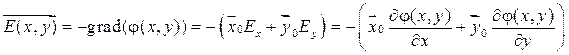




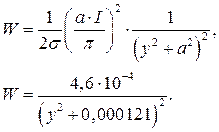







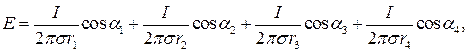 ,
,