
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электроемкость уединенного проводника и ее физический смысл. Коэффициенты емкости и взаимной емкости проводниковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Опыты показывают, что изменение заряда проводника приводит к изменению его потенциала, а отношение изменения заряда ∆ q к изменению потенциала f для данного проводника остается величиной постоянной. Следовательно, каждый проводник можно характеризовать отношением
которое и называется электроемкостью уединенного проводника. В выражении (19.16) k - коэффициент пропорциональности, зависящий от выбора системы единиц измерения физических величин. В системе СИ: k = 1,
Таким образом, электроемкость уединенного проводника это физическая величина, численно равная количеству электричества, на которое необходимо изменить заряд проводника, чтобы его потенциал изменился на единицу. В этом и заключается физический смысл электроемкости уединенного проводника. При q = 0, j = 0, а ∆q пропорционально ∆j, то и q j, следовательно,
В системе СИ
Экспериментальные данные говорят о том, что электроемкость (емкость) проводника зависит только от формы его поверхности, линейных размеров, расположения проводника относительно других проводников и диэлектрической проницаемости среды окружающей проводник. За единицу емкости принимается емкость такого проводника, потенциал которого изменяется на единицу при изменении его заряда на единицу. В системе СИ единицей емкости является 1 Ф (Фарада). 1 Ф = 1 Кл/В = 10-6 мкФ = 10-12 пФ.
Конденсаторы и их емкость Отдельно взятые проводники обладают малой емкостью. Увеличить емкость проводника можно приблизив к нему другой проводник. Полученное устройство называют конденсатор. Конденсаторы, принебольших потенциалах способны накапливать ("конденсировать") значительные по величине заряды. Образующие конденсатор проводники называют обкладками или пластинами. На обкладках конденсаторов накапливаются равные по величине но противоположные по знаку заряды. Под электроемкостью (емкостью) конденсатора подразумевают физическую величину, численно равную отношению величины заряда одного знака к разности потенциалов между обкладками:
Емкость конденсаторов измеряется в тех же единицах, что и емкость проводника. Величина емкости конденсатора определяется его геометрическими размерами, формой и диэлектрической проницаемостью среды, заполняющей пространство между обкладками. Наибольшее распространение получили плоские, цилиндрические и сферические конденсаторы.
Емкость плоского конденсатора. Плоский конденсатор представляет собой две пластины, расположенные на некотором расстоянии друг от друга, пространство между которыми заполнено слоем диэлектрика. Если площадь одной из обкладок S, а заряд на ней q,то напряженность электрического поля между обкладками
но
где d - расстояние между обкладками, следовательно
откуда
Из (2.24) видно, что емкость плоского конденсатора действительно зависит от его геометрических размеров и диэлектрической проницаемости среды, заполняющей пространство между обкладками, кроме того из нее можно получить размерность диэлектрической проницаемости вакуума:
Цилиндрический конденсатор. Цилиндрический конденсатор представляет собой устройство из двух цилиндрических обкладок, имеющих общую ось (коаксиальных), разделенных слоем диэлектрика цилиндрической формы. Электрическое поле такого конденсатора представляет собой суперпозицию двух полей цилиндрических поверхностей, имеющих равные по величине, но противоположные по знаку заряды. Напряженность такого электрического поля
Разность потенциалов между обкладкам
где R1 и R2 - соответственно радиусы внутренней и внешней обкладок. Таким образом
При d = R2 - R1 << R1
где d = R2 - R1 - расстояние между обкладками. Тогда
Следовательно, при указанных условиях, емкость цилиндрического конденсатора с определенной степенью точности можно рассчитывать по формуле емкости плоского конденсатора. 19.4.3. Сферический конденсатор Сферический конденсатор представляет собой устройство, состоящее из двух сферических поверхностей, которые имеют общий центр, различных радиусов, разделенных сферическим слоем диэлектрика. Напряженность электрического поля между обкладками такого конденсатора
Разность потенциалов между обкладками
Таким образом
При R2 - R1 = d << R1 R2
т.е. емкость сферического конденсатора можно с определенной степенью точности рассчитывать по формуле емкости плоского конденсатора.
Соединения конденсаторов. Отдельные конденсаторы обладают определенной емкостью и могут работать только при подключении их к характерным для них напряжениям, которые определяются свойствами и толщиной диэлектрика. Если напряжение превышает допустимое - происходит пробой конденсатора. Поэтому очень часто из имеющихся в наличии конденсаторов собирают батарею необходимой емкости и предназначенную для работы при более высоких напряжениях. Существует два вида соединения конденсаторов: последовательное и параллельное.
|
||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 801; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

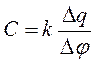 или
или  , 2.16
, 2.16 или
или 
 2.18
2.18 2.19
2.19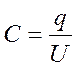
 ,
, ,
, ,
,
 2.25
2.25

 2.27
2.27
 , 2.29
, 2.29
 2.31
2.31 2.32
2.32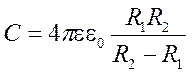
 ,
,


