
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проводники в электрическом поле. Емкость, конденсаторы. Энергия электрического поля в конденсаторе.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Проводники в электрическом поле. По своим электрическим свойствам все вещества можно разделить на проводники и диэлектрики. В проводниках под действием постоянного электрического поля возникает электрический ток, в диэлектриках – нет. Это объясняется принципиальным различием их структуры. В проводниках существуют носители тока, или свободные заряды, т.е. заряженные частицы, которые под действием поля могут перемещаться в пределах проводника. В диэлектриках таких свободных зарядов нет, все заряженные частицы удерживаются в пределах атомов, молекул, ионов и под действием поля испытывают лишь микроскопические смещения. Если сообщить проводнику заряд или поместить его во внешнее электростатическое поле, то через достаточно короткий промежуток времени в проводнике установится равновесное распределение заряда, при котором электрический ток отсутствует. Если нейтральный проводник поместить во внешнее электростатическое поле, то в нем произойдет перераспределение зарядов – явление электростатической индукции – т.о., что поле индуцированных зарядов скомпенсирует внешнее поле внутри проводника. Напряженность на поверхности проводника перпендикулярна этой поверхности, поскольку последняя является эквипотенциальной, причем Е = σ/ε0. Электроемкость. Т.к. в условиях электростатического равновесия значения потенциала во всех точках проводника одинаковы, можно говорить, что потенциал φ проводника пропорционален заряду: φ = q/C. Отношение заряда к потенциалу является для данного проводника постоянной величиной – электрической емкостью проводника: С = q/φ. Емкость зависит от размеров и форм проводника и не зависит от материала, т.к. существует единственное распределение заданного заряда по заданной поверхности, при котором всюду Е = 0. Емкость численно равна заряду, который необходимо сообщить проводнику, чтобы увеличить его потенциал на единицу. Конденсатор – система, состоящая из 2-х проводников, которым сообщены заряды одинаковой абсолютной величины, но противоположных знаков. Обкладки – проводники в форме тонких пластин той или иной формы. Пространство между ними заполнено диэлектриком. Разность потенциалов между обкладками - напряжение между обкладками. U = Ed = (σ/ε0 )d, где d – расстояние между обкладками. C = q/U – емкость конденсатора. С = ε0S/d. если пространство между обкладками заполнено однородным диэлектриком с диэлектрической проницаемостью ε, то С = εε0S/d. Энергия электрического поля. Энергия заряженного конденсатора – энергия его электрического поля. Для его описания вводится плотность энергии поля – энергия поля в единице объёма: ω=ΔW/ΔV, ΔW – энергия поля в этом объёме ΔV. При пренебрежении краевыми эффектами, электрическое поле конденсатора сосредоточено в пространстве между обкладками и однородно, поэтому плотность энергии одинакова во всех точках между обкладками и равна отношению полной энергии поля к объёму пространства, которое оно занимает: ω = W/V = εε0E²/2. По закону сохранения энергии работа, совершенная при разрядке конденсатора, определяет энергию, которой он обладал. Энергия заряженного конденсатора может быть представлена в виде: W = CU2/2 = q2/2C = εε0E²V/2.
5. Постоянный электрический ток. Закон Ома в дифференциальной форме. Электродвижущая сила.
Электрическим током называется упорядоченное движение электрических зарядов. Условия существования электрического тока: 1) наличие свободных зарядов в проводнике; 2) наличие электрического поля внутри проводника. Сила тока - скалярная величина, равная отношению величины заряда, протекающего через поперечное сечение проводника за некоторый интервал времени, к величине этого интервала. Для постоянного тока, т. е. тока, не изменяющегося со временем, справедлива следующая формула: I=q/t. Напряжением на участке U называется отношение работы электростатических и сторонних сил, действующих на переносимый заряд, к величине этого заряда. Закон Ома в дифференциальной форме. Закон Ома в дифференциальной форме справедлив для любой точки участка цепи как с постоянным, так и с переменным сечением. Для однородного участка цепи плотность тока равна
Подставим эту формулу, а также формулу для сопротивления (2.26) в закон Ома (2.24)
Величина, обратная удельному сопротивлению, называется удельной проводимостью, т. е.
Формула (2.28) выражает закон Ома в дифференциальной форме. Плотность тока пропорциональна напряженности электрического поля и имеет одинаковое с ней направление (рис. 2.8).
В такой форме закон Ома выражает связь между величинами, относящимися к данной точке, и поэтому применим к неоднородным проводникам. ε (э.д.с.) - работа сторонних сил по перемещению единичного положительного заряда по участку цепи
По аналогии с электрическим полем (см. формулу (2.3)), вводится понятие напряженность поля сторонних сил:
Тогда для любой точки участка цепи, содержащего ЭДС (рис. 2.9), справедлив закон Ома в дифференциальной форме (см. (2.28))
В интегральной форме закон Ома для участка цепи, содержащего ЭДС (участок 1 - ε – 2 на рис. 2.9), имеет вид
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.2.239 (0.006 с.) |

 ; отсюда:
; отсюда:  .
. Учтем, что для однородного поля справедлива формула (2.19)
Учтем, что для однородного поля справедлива формула (2.19)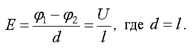 Тогда
Тогда
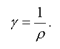 В векторной форме формулу (2.27) можно записать следующим образом
В векторной форме формулу (2.27) можно записать следующим образом
 Рис.2.8
Рис.2.8


 Рис.2.9
Рис.2.9 где R1-2 - сопротивление участка 1 - ε - 2;
где R1-2 - сопротивление участка 1 - ε - 2; 
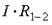 - падение напряжения (напряжение).
- падение напряжения (напряжение).


