
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 5. Проводники в электростатическом полеСодержание книги
Поиск на нашем сайте
Проводники - это вещества, в которых есть свободные носители зарядов, способные перемещаться под действием электрического поля. В случае металлических проводников свободными носителями заряда являются валентные электроны. Далее будем говорить о металлических проводниках, в которых носителями свободных зарядов являются электроны. Электроны в проводнике способны перемещаться под действием сколь угодно малой силы т.к. 1) напряженность поля внутри проводника равнялась нулю: Поскольку Из (2) следует, что поверхность проводника и весь проводник являются эквипотенциальной поверхностью; 2) напряженность поля на поверхности проводника должна быть в каждой точке направлена по нормали к поверхности, т. е. 3) Поскольку внутри заряженного проводника электрическое поле отсутствует, то согласно теореме Гаусса – Остроградского, это означает, что сумма зарядов внутри него равна нулю. Следовательно, все (нескомпенсированные) заряды располагаются на поверхности проводника с поверхностной плотностью Используя теорему Гаусса-Остроградского, легко показать, что вблизи поверхности заряженного проводника E = Проводник во внешнем электростатическом поле
Электрическая емкость Будем сообщать уединенному проводнику разные по величине заряды Это отношение дает величину электроемкости уединенного проводника, т.е. C=q/ Электрическая емкость измеряется в фарадах: 1Ф= 1Кл / 1В, а также в мФ, мкФ, нФ, пФ...; причем 1мФ = 10-3 Ф, 1мкФ = 10 Потенциал заряженного шара радиуса R равен т.е. оказывается, что С пропорциональна радиусу шарового проводника R. Подсчитаем емкость Земного шара, имеющего радиус
Для плоского конденсатора, (см. рис. 2), тогда по формуле (7) можно найти где На электрических схемах электрические конденсаторы обозначают так: a) рис. 3. а - конденсатор постоянной емкости, б) рис. 3.б- конденсатор переменной емкости, в) рис. 3. в - подстроечный конденсатор.

Используя формулу (7), находим, что UСΣ= UC1+UC2+…+ UCn, откуда СΣ= C1+C2+…+ Cn=ΣCi (9) При последовательном соединении конденсаторов, (см. рис. 5) UΣ= U1+U2+…+ Un, что согласно (7) можно переписать так т.е. суммарная емкость уменьшается. Энергия заряженного проводника, системы проводников и конденсатора Пусть проводник имеет емкость С, заряд q, потенциал Чтобы зарядить проводник от нуля до потенциала
Энергия заряженного проводника полная энергия системы заряженных проводников Для конденсатора
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.35.234 (0.005 с.) |

 , то для равновесия (покоя) электронов в проводнике необходимо, чтобы:
, то для равновесия (покоя) электронов в проводнике необходимо, чтобы: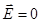 . (1)
. (1)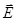 = -grad
= -grad  , [см. (3.14)], то равенство нулю
, [см. (3.14)], то равенство нулю 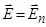 , а касательная составляющая
, а касательная составляющая  (3)
(3) .
. . (4)
. (4)

 При внесении незаряженного проводника в электрическое поле, изображенное штриховыми линиями на рис. 1, положительные заряды будут перемещаться по направлению
При внесении незаряженного проводника в электрическое поле, изображенное штриховыми линиями на рис. 1, положительные заряды будут перемещаться по направлению 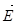 , а отрицательные – против поля
, а отрицательные – против поля  и линии напряженности будут разорваны поверхностью проводника, заканчиваясь на индуцированных отрицательных зарядах и начинаясь на индуцированных положительных (см. рис. 1, сплошные линии).
и линии напряженности будут разорваны поверхностью проводника, заканчиваясь на индуцированных отрицательных зарядах и начинаясь на индуцированных положительных (см. рис. 1, сплошные линии). При этом проводник будет иметь разные по величине потенциалы
При этом проводник будет иметь разные по величине потенциалы  .Оказывается отношение
.Оказывается отношение 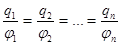 - есть величина постоянная для данного проводника и не зависит от величины сообщенного заряда, а зависит только от геометрической формы проводника и диэлектрической проницаемости окружающей его среды.
- есть величина постоянная для данного проводника и не зависит от величины сообщенного заряда, а зависит только от геометрической формы проводника и диэлектрической проницаемости окружающей его среды. Ф, 1 нФ =
Ф, 1 нФ = 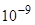 Ф, 1 пФ =
Ф, 1 пФ =  Ф.
Ф. , с учетом этого находим емкость уединненого шарового проводника:
, с учетом этого находим емкость уединненого шарового проводника:  , (6)
, (6) км
км 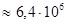 м.
м. Ф = 700 мкФ.
Ф = 700 мкФ.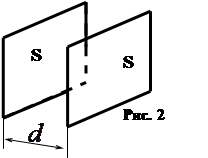 Для получения большей емкости используют конденсаторы в виде двух проводников, помещенных близко друг от друга. В этом случае емкость
Для получения большей емкости используют конденсаторы в виде двух проводников, помещенных близко друг от друга. В этом случае емкость 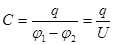 . (7)
. (7)
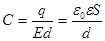 , (8)
, (8) – диэлектрическая проницаемость вещества между пластинами.
– диэлектрическая проницаемость вещества между пластинами.
 С1 С2 Сn
С1 С2 Сn









 При параллельном соединении конденсаторов, (см. рис. 4) общий заряд qΣ= q1+q2+…+qn.
При параллельном соединении конденсаторов, (см. рис. 4) общий заряд qΣ= q1+q2+…+qn. , откуда
, откуда 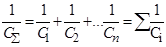 , (10)
, (10) ; тогда работа, совершаемая против сил электрического поля при перенесении заряда
; тогда работа, совершаемая против сил электрического поля при перенесении заряда  из бесконечности на проводник, будет
из бесконечности на проводник, будет 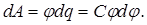 (11)
(11)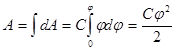 . (12)
. (12)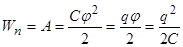 ,
, . (13)
. (13)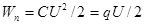 . (14)
. (14)


