Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 8. Магнитное поле в вакуумеСодержание книги
Поиск на нашем сайте
Магнитный момент контура с током. Магнитная индукция Опыт показывает, что электрические токи взаимодействуют между собой, напрмер, токи I
Вращающий момент, действующий на контур, зависит как от свойств магнитного поля в данной точке, так и от свойств контура. Оказывается, что максимальная величина вращающего момента пропорциональна IS, т.е. M называют магнитным моментом контура, который в СИ измеряется в А×м2. На пробные контуры с разными рm, помещаемыми в данную точку магнитного поля, будут действовать разные по величине максимальные вращающие моменты М В = М Магнитная индукция есть вектор, направление которого совпадает с направлением нормали контура с током, свободно установившегося во внешнем магнитном поле(см.рис.2)
На контур с током, помещенный в магнитное поле с индукцией Величина его M = при Закон Ампера Ампер нашел, что на элемент тока Id Произведение I Закон Био-Савара – Лапласа Био, Савар и Лаплас установили закон, который позволяет вычислить магнитную ин дукцию поля, созданного элементом тока Id

 
  т.е. индукция магнитного поля, создаваемого элементом тока Id т.е. индукция магнитного поля, создаваемого элементом тока Id  в точке А, (см. рис. 3), на расстоянии r от него, пропорциональна величине элемента тока и синусу угла a, равного углу между направлениями элемента тока Id в точке А, (см. рис. 3), на расстоянии r от него, пропорциональна величине элемента тока и синусу угла a, равного углу между направлениями элемента тока Id  и и  , а также обратно пропорциональна квадрату расстояния между ними; , а также обратно пропорциональна квадрату расстояния между ними;  Гн / м - магнитная постоянная. Гн / м - магнитная постоянная.
Закон Био-Савара – Лапласа в векторной форме имеет вид: d Закон Био-Савара – Лапласа позволяет вычислить магнитную индукцию поля любых систем токов, используя принцип суперпозиции магнитных поля Применим закон Био-Савара – Лапласа и принцип суперпозиции (7) к расчету магнитных полей следующих токов: 8.3.1. Поле прямого тока:
Рис. 4 | Из рис. 4 с учетом (6) находим, что d   плоскости, в которой лежат d плоскости, в которой лежат d  и и  ; далее можно найти ; далее можно найти  ,откуда, принимая во внимание, что ,откуда, принимая во внимание, что  получаем получаем  . С учетом этого из (5) находим: . С учетом этого из (5) находим:
 интегрируя последнее равенство, получаем:
интегрируя последнее равенство, получаем:
|
 (8)
(8)
Для бесконечно длинного проводника  ,
,  и из (8) следует, что
и из (8) следует, что
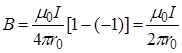 . (9)
. (9)
C учетом (4) и (9) cила взаимодействия двух бесконечно длинных тонких и параллельных проводников  . (10)
. (10)
Пусть I1 = I2 = I, r0 = 1м, l = 1м, F =  Н, тогда I = 1 А. Это было строгое определение единицы силы тока - ампера.
Н, тогда I = 1 А. Это было строгое определение единицы силы тока - ампера.
 8.3.2. Поле кругового тока
8.3.2. Поле кругового тока
|
 Можно показать, что магнитная индукция поля, созданного круговым током радиуса R, на расстоянии r0 вдоль перпендикуляра, восстановленного из центра контура, (см. рис.5), будет
Можно показать, что магнитная индукция поля, созданного круговым током радиуса R, на расстоянии r0 вдоль перпендикуляра, восстановленного из центра контура, (см. рис.5), будет  (11)
(11)|
|
В частности, в центре кругового тока  ,
,
|
|
 . (12)
. (12)
Для плоской катушки, состоящей из N, витков магнитная индукция на оси катушки
 . (13)
. (13)
При больших расстояниях от контура, (рис. 5), т. е. при r0 >> R из (11) получим
 (14)
(14)
Лекция 9. Магнитное поле в вакууме (продолжение)
|
| Поделиться: |

 притягиваются, а токи I
притягиваются, а токи I  отталкиваются. Взаимодействие токов осуществляется через поле, которое называется магнитным. Следовательно, движущиеся заряды (токи) изменяют свойства окружающего их пространства - создают в нем магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы. Подобно тому, как для исследования электрического поля мы использовали пробный заряд, применим для исследования магнитного поля пробный ток, циркулирующий в плоском замкнутом контуре очень малых размеров. Будем называть такой контур пробным контуром.
отталкиваются. Взаимодействие токов осуществляется через поле, которое называется магнитным. Следовательно, движущиеся заряды (токи) изменяют свойства окружающего их пространства - создают в нем магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы. Подобно тому, как для исследования электрического поля мы использовали пробный заряд, применим для исследования магнитного поля пробный ток, циркулирующий в плоском замкнутом контуре очень малых размеров. Будем называть такой контур пробным контуром. Ориентацию его в пространстве характеризует направление нормали
Ориентацию его в пространстве характеризует направление нормали  к контуру, восстанавливаемой по правилу правого буравчика: вращаем рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали
к контуру, восстанавливаемой по правилу правого буравчика: вращаем рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали  (см. рис. 1). Помещая пробный контур в магнитное поле, обнаружим, что поле стремится повернуть контур (нормаль) в определенном направлении.
(см. рис. 1). Помещая пробный контур в магнитное поле, обнаружим, что поле стремится повернуть контур (нормаль) в определенном направлении. ~ IS, где I -ток контуре, S - площадь контура с током (рис. 1). Векторную величину
~ IS, где I -ток контуре, S - площадь контура с током (рис. 1). Векторную величину  (1)
(1) будет для всех контуров одинаково, оно будет являться силовой характеристикой магнитного поля, которая называется магнитной индукцией
будет для всех контуров одинаково, оно будет являться силовой характеристикой магнитного поля, которая называется магнитной индукцией /р
/р  Поле вектора В можно представить с помощью силовых линий (см. рис. 2), как и поле вектора
Поле вектора В можно представить с помощью силовых линий (см. рис. 2), как и поле вектора 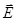 ; таким образом В является аналогом Е. Магнитная индукция в СИ измеряется в теслах: 1 Тл= 1 Нм/ 1 А×м2. Тесла равен магнитной индукции однородного поля, в котором на плоский контур с током, который имеет магнитный момент 1 Ам2, действует максимальный вращающий момент, равный 1 Нм.
; таким образом В является аналогом Е. Магнитная индукция в СИ измеряется в теслах: 1 Тл= 1 Нм/ 1 А×м2. Тесла равен магнитной индукции однородного поля, в котором на плоский контур с током, который имеет магнитный момент 1 Ам2, действует максимальный вращающий момент, равный 1 Нм.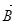 , действует вращающий момент
, действует вращающий момент  . (3)
. (3)
 имеем М = M
имеем М = M  = 0 или
= 0 или 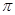 , M= 0.
, M= 0.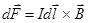 . (4)
. (4) называют элементом тока, где
называют элементом тока, где  от него:
от него: dB =
dB = 
 , (5)
, (5)
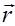

 . (6)
. (6) =
=  . (7)
. (7)













 .
.








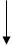 I
I