
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Гаусса-ОстроградскогоСодержание книги
Поиск на нашем сайте
Площадь ее поверхности
Можно показать, что поток через замкнутую поверхность не зависит от формы поверхности и от расположения зарядов в ней.
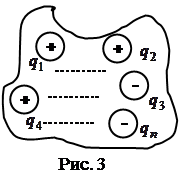
Рассмотрим поток, создаваемый системой зарядов, сквозь замкнутую поверхность произвольной формы, внутри которой они находятся (рис.3):
Итак, мы доказали теорему Гаусса — Остроградского: «полный поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на Теорему Гаусса — Остроградского, (5), можно записать в дифференциальной форме:
где
Из теоремы Гаусса — Остроградского вытекают следствия: 1) линии вектора Теорема Гаусса позволяет рассчитать электрические поля, создаваемые заряженными телами различной формы: 2.2.1.Поле равномерно заряженной, бесконечно протяженной плоскости (рис. 5). Построим цилиндр, ось которого перпендикулярна к поверхности, и применим теорему Гаусса-Остроградского
т.к. то отсюда
где s = q/S поверхностная плотность заряда, измеряемая в СИ в Кл/м2.
Итак: По этой же формуле определяется напряженность электрического поля вблизи заряженного проводника.
где t = q/ h — линейная (погонная) плотность заряда, которая измеряется в Кл/м. Когда r < R, то 2.2.4 Поле заряженной сферы: поток вектора
при r < R имем
3.1. Работа сил электрического поля: 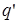 на расстояние d: на расстояние d:
Таким образом, работа, совершаемая силами поля, не зависит от формы пути, по которому перемещался заряд, а зависит только от расстояния d, измеряемого вдоль силовой линии между начальным и конечным положением заряда.
И в этом случае работа сил не зависит от формы пути. Она является только функцией начального и конечного положения заряда. Для замкнутой траектории L она равна нулю, т. к.
т.е. ЦИРКУЛЯЦИЯ ВЕКТОРА НАПРЯЖЕННОСТИ ПО ЛЮБОМУ ЗАМКНУТОМУ КОНТУРУ РАВНА НУЛЮ. В механике было приведено следующее определение: «Силы, работа которых не зависит от формы пути, называются консервативными силами, а поля, работа сил которых не зависит от формы пути, называются потенциальными полями». Таким образом, рассмотренное нами электростатическое поле является потенциальным, а кулоновские силы - консервативными.
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.005 с.) |

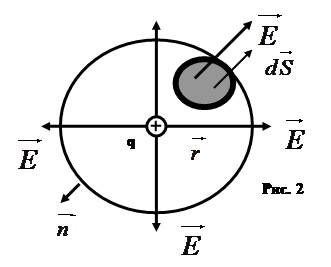 Найдем поток вектора напряженности электрического поля, создаваемого точечным зарядом q, через сферическую поверхность радиуса r.
Найдем поток вектора напряженности электрического поля, создаваемого точечным зарядом q, через сферическую поверхность радиуса r.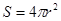 . Силовые линии электрического поля, (см. рис. 2), идут по радиусам к поверхности сферы и поэтому угол между векторами
. Силовые линии электрического поля, (см. рис. 2), идут по радиусам к поверхности сферы и поэтому угол между векторами 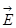 и
и  равен нулю.
равен нулю.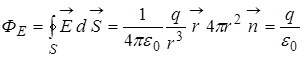 . (4)
. (4)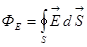 .
. Согласно принципу суперпозиции
Согласно принципу суперпозиции 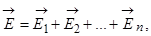 поэтому
поэтому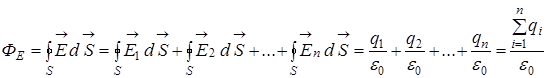 таким образом
таким образом 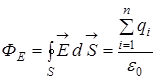 . (5)
. (5)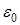 ».
».
 , (6)
, (6)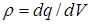 - объемная плотность заряда.
- объемная плотность заряда.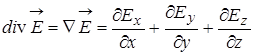 , знак
, знак 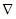 - оператор набла.
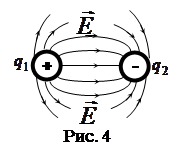
- оператор набла.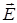 (силовые линии) нигде, кроме зарядов, не начинаются и не заканчиваются: они, начавшись на заряде, уходят в бесконечность для положительного заряда, либо, приходя из бесконечности, заканчиваются на отрицательном заряде (картина силовых линий приводится на рис. 4); 2) если алгебраическая сумма зарядов, охватываемых замкнутой поверхностью, равна нулю, то полный поток через эту поверхность равен нулю; 3) если замкнутая поверхность проведена в поле так, что внутри нее нет зарядов, то число входящих линий вектора напряженности равно числу выходящих и поэтому полный поток через такую поверхность равен нулю.
(силовые линии) нигде, кроме зарядов, не начинаются и не заканчиваются: они, начавшись на заряде, уходят в бесконечность для положительного заряда, либо, приходя из бесконечности, заканчиваются на отрицательном заряде (картина силовых линий приводится на рис. 4); 2) если алгебраическая сумма зарядов, охватываемых замкнутой поверхностью, равна нулю, то полный поток через эту поверхность равен нулю; 3) если замкнутая поверхность проведена в поле так, что внутри нее нет зарядов, то число входящих линий вектора напряженности равно числу выходящих и поэтому полный поток через такую поверхность равен нулю.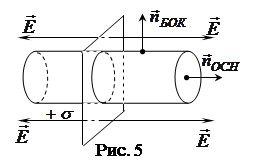
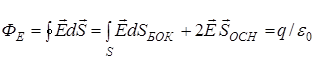 ,
,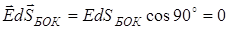 ,
,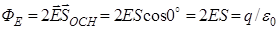
 , (7)
, (7) 2.2.2. Поле между двумя бесконечно протя ж енными, разноименно заряженными параллельными плоскостями, (см. рис. 6). Вне внутреннего промежутка,
2.2.2. Поле между двумя бесконечно протя ж енными, разноименно заряженными параллельными плоскостями, (см. рис. 6). Вне внутреннего промежутка, 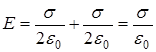 .
.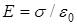 . (8)
. (8) 2.2.3. Поле заряженного цилиндра: заряженный цилиндр радиуса R, (см. рис. 7), окружим коаксиальной цилиндрической поверхностью радиуса r; поток вектора
2.2.3. Поле заряженного цилиндра: заряженный цилиндр радиуса R, (см. рис. 7), окружим коаксиальной цилиндрической поверхностью радиуса r; поток вектора 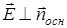 , где
, где  – внешняя нормаль к основаниям цилиндра; поток через боковую поверхность
– внешняя нормаль к основаниям цилиндра; поток через боковую поверхность  , здесь h – высота цилиндра. Согласно теореме Гаусса – Остроградского, при
, здесь h – высота цилиндра. Согласно теореме Гаусса – Остроградского, при 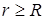

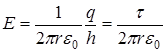 , (9)
, (9)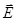 через поверхность сферы радиуса r,
через поверхность сферы радиуса r,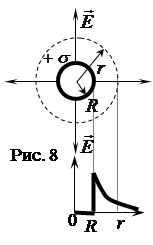
 (см. рис. 8, вверху), которая окружает заряженную сферу, имеющую радиус R,при r
(см. рис. 8, вверху), которая окружает заряженную сферу, имеющую радиус R,при r 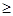 R
R 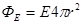 . По теореме Гаусса – Остроградского
. По теореме Гаусса – Остроградского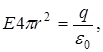 oткуда
oткуда  (10)
(10)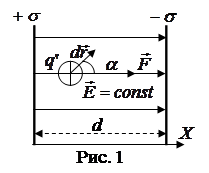 Лекция 3. Потенциал электрического поля
Лекция 3. Потенциал электрического поля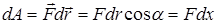 ,
, 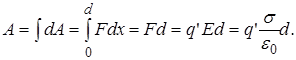
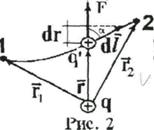 3.1.2. В неоднородном поле точечного заряда q (см. рис. 2) Найдем работу по перемещению пробного заряда
3.1.2. В неоднородном поле точечного заряда q (см. рис. 2) Найдем работу по перемещению пробного заряда 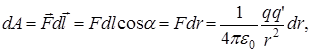
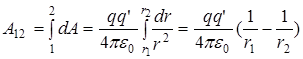 . (2)
. (2)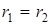 , т. е.
, т. е. или
или 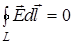 , (3)
, (3)


