
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
L. 3. Напряженность электрического поляСодержание книги
Поиск на нашем сайте
Взаимодействие между покоящимися зарядами осуществляется через электрическое поле, т.к. всякий электрический заряд изменяет свойства окружающего его пространства, создавая в нем электрическое поле. Это поле проявляет себя в том, что оно действует с силой на заряд, внесенный в него. Основной количественной характеристикой электрического поля является напряженность электрического поля
  (малый потому, чтобы не изменять ни величины, ни распреде- (малый потому, чтобы не изменять ни величины, ни распреде-
Рис. 2 силе, с которой электрическое поле действует на единичный положительный заряд и совпадает по направлению с этой силой, (см. рис. 2.) Напряженность электрического поля измеряется в В/м. В общем случае на заряд q, находящийся в поле с напряженностью Исследуем с помощью пробного заряда q' поле неподвижного заряда q. Согласно закону Кулона на пробный заряд q' со стороны заряда q будет действовать сила (2); с учетом этого напряженность поля, создаваемого точечным зарядом q, здесь Таким образом, напряженность электрического поля, создаваемого точечным зарядом q на расстоянии r от него, прямо пропорциональна величине заряда q и обратно пропорциональна r 2 - квадрату расстояния от него. Принцип суперпозиции электрических полей Если электрическое поле создается совокупностью точечных зарядов q1, q2,..., qn, то оно будет действовать на пробный заряд q' в некоторой точке поля М с результирующей силой
Это утверждение носит название принципа суперпозиции (наложения) электрических полей и справедливо для не очень больших величин Электрический диполь Два точечных заряда, равных по величине и противоположных по знаку, находящихся на некотором расстоянии друг от друга, называются электрическим диполем (см. рис. 4). Плечом диполя называется вектор
Рис. 4 Приведем формулы для напряженности поля диполя: 1)в точке А, расположенной на оси диполя, (см. рис. 5)
На диполь, помещенный в электрическое поле с напряженностью
  который стремится установить диполь по полю, (см. рис.6). который стремится установить диполь по полю, (см. рис.6).
Потенциальная энергия диполя во внешнем
 
 . (13) . (13)
Лекция 2. Поток вектора напряженности. Теорема Гаусса — Остроградского Поток вектора напряжения Чтобы продвинуться дальше в изучении электрического поля, необходимо использовать векторный анализ — математический аппарат. Мы должны знать, что такое градиент, ротор, дивиргенция. Начнем же с понятия “поток вектора

        
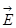 , которое пронизывает некоторую плоскую поверхность площади S, тогда скаляр- , которое пронизывает некоторую плоскую поверхность площади S, тогда скаляр-
ное произведение где В общем случае поле может быть неоднородным, поверхность неплоской. В этом случае поверхность можно мысленно разбить на бесконечно малые элементарные площадки dS, которые можно считать плоскими, а поле вблизи них однородным. В таком случае поток через элементарную площадку Полный поток вектора напряженности через поверхность S
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.179.30 (0.006 с.) |

 . (4)
. (4)


 ления тех сторонних зарядов, которые порождают исследуемое
ления тех сторонних зарядов, которые порождают исследуемое
 поле). Таким образом, напряженность электрического поля равна
поле). Таким образом, напряженность электрического поля равна . (5)
. (5) , (6)
, (6) - радиус-вектор, проведенный от заряда q в рассматриваемую точку поля.
- радиус-вектор, проведенный от заряда q в рассматриваемую точку поля. [см. (З)]. Напряженность поля в этой точке
[см. (З)]. Напряженность поля в этой точке (7)
(7) т.е, равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов в отдельности. Таким образом,
т.е, равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов в отдельности. Таким образом, (8)
(8) , направленный по оси диполя от отрицательного заряда к положительному и по модулю равный расстоянию между ними. Электрический диполь характеризуется моментом диполя
, направленный по оси диполя от отрицательного заряда к положительному и по модулю равный расстоянию между ними. Электрический диполь характеризуется моментом диполя  . (9)
. (9)


 В соответствии с принципом суперпозиции напряженность
В соответствии с принципом суперпозиции напряженность

 q q в произвольной точке поля диполя
q q в произвольной точке поля диполя  . (10)
. (10) 2) в точке, расположенной на перпендикуляре к середине его оси
2) в точке, расположенной на перпендикуляре к середине его оси . (11)
. (11) , (12)
, (12)








 будет называться потоком вектора напряженности
будет называться потоком вектора напряженности  , (1)
, (1) — есть вектор, равный произведению величины площади на нормаль к этой поверхности, Еn –проекция вектора
— есть вектор, равный произведению величины площади на нормаль к этой поверхности, Еn –проекция вектора  к площадке.
к площадке. . (2)
. (2) . (3)
. (3)


