
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электродвижущая сила источника тока. НапряжениеСодержание книги
Поиск на нашем сайте
Для того, чтобы поддерживать ток неизменным, необходимо от конца проводника, (см. рис. 2), с меньшим потенциалом большим потенциалом Это возможно лишь за счет работы сторонних сил неэлектростатической природы, например, за счет протекания химических процессов в гальванических элементах. Величина, численно равная работе сторонних сил, по перемещению единичного положительного заряда называется ЭДС и обозначается ЭДС, как и потенциал, в СИ измеряется в вольтах. Представим стороннюю силу как
тогда работа сторонних сил на участке 1-2 цепи будет равна
а ЭДС на этом же участке где dl - элемент длины проводящего участка цепи. ЭДС, действующая в замкнутой цепи
т.е. ЭДС равна циркуляции вектора напряженности сторонних сил. Однако, кроме сторонних сил, на носители тока действуют силы электростатического поля qE. Следовательно, результирующая сила, действующая в каждой точке цепи на заряд Работа, совершаемая этой силой над зарядом q на участке 1-2 цепи, рис. 2,
Величина, численно равная работе, совершаемой электрическими и сторонними силами над единичным положительным зарядом, называется падением напряжения или просто напряжением U на данном участке, т. е. U Участок цепи, на котором не действуют сторонние силы, называется однородным. Для него U Участок цепи, на котором действуют сторонние силы, называется неоднородным. Для замкнутой цепи ( 3. Закон Ома для однородного участка цепи и закон Ома в дифференциальной форме 3.1. Ом в 1826 г. экспериментально установил закон, который называется законом Ома для однородного участка цепи: ТОК, ТЕКУЩИЙ ПО ОДНОРОДНОМУ МЕТАЛЛИЧЕСКОМУ ПРОВОДНИКУ, ПРОПОРЦИОНАЛЕН ПАДЕНИЮ НАПРЯЖЕНИЯ U НА ПРОВОДНИКЕ", т. е. I = где R - сопротивление проводника, измеряется в СИ в омах (Ом); из (14) следует, что 1Ом =1 В/1 А. Сопротивление проводника R =ρl / S, (15) где р - удельное сопротивление, измеряется в СИ вОм ×м.
уменьшается до нуля. Это явление называется сверхпроводимостью. Закон Ома в дифференциальной форме
Между концами проводника длиной dl напряжение U = Edl, под действием которого через его поперечное сечение площадью dS течет ток I = jdS. Сопротивление цилиндрического проводника, в нашем случае, равно R = где где n - концентрация свободных электронов, она может достигать 10 < v > – средняя скорость теплового движения электрона, k = 1,38 ×10
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |



 Если в проводнике создать электрическое поле и затем не поддерживать его неизменным, то за счет перемещения зарядов поле исчезнет и, следовательно, ток прекратится.
Если в проводнике создать электрическое поле и затем не поддерживать его неизменным, то за счет перемещения зарядов поле исчезнет и, следовательно, ток прекратится. отводить приносимые туда током заряды и переносить их к началу проводника с
отводить приносимые туда током заряды и переносить их к началу проводника с ,т.е. необходимо создать круговорот зарядов.
,т.е. необходимо создать круговорот зарядов. :
: 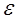 = AСТОР/q. (6)
= AСТОР/q. (6) , (7)
, (7) , (8)
, (8) =
=  ,
, , (9)
, (9) . (10)
. (10)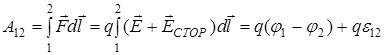 . (11)
. (11) = A
= A  +
+ 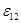 . (12)
. (12) . (13)
. (13) .
. (
( Оно зависит от температуры:
Оно зависит от температуры:  =
= 
 T, где
T, где  - температурный коэффициент сопротивления, близкий к 1/273 К
- температурный коэффициент сопротивления, близкий к 1/273 К  , T – термодинамическая температура; так что с ростом температуры сопротивление металлических проводников увеличивается. Качественная температурная зависимость удельного сопротивления металлического проводника от Т представлена на рис. 3. Сопротивление многих металлов и их сплавов при очень низких температурах Тk (0,14 – 20 K), называемых критическими, скачкообразно
, T – термодинамическая температура; так что с ростом температуры сопротивление металлических проводников увеличивается. Качественная температурная зависимость удельного сопротивления металлического проводника от Т представлена на рис. 3. Сопротивление многих металлов и их сплавов при очень низких температурах Тk (0,14 – 20 K), называемых критическими, скачкообразно Найдем связь между векторами
Найдем связь между векторами  и
и  . Для этого мысленно выделим в окрестности некоторой точки проводника элементарный цилиндрический объем с образующими, параллельными векторам
. Для этого мысленно выделим в окрестности некоторой точки проводника элементарный цилиндрический объем с образующими, параллельными векторам  .Используя закон Ома для участка цепи I =
.Используя закон Ома для участка цепи I = 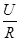 , находим: jdS =
, находим: jdS =  , откуда и получаем закон Ома в дифференциальной форме
, откуда и получаем закон Ома в дифференциальной форме  =
= 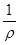
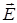 =
=  , (16)
, (16) =
=  удельная электропроводность; [
удельная электропроводность; [  , (17)
, (17)
 10
10  электрон / м
электрон / м  ; e – заряд электрона, m – его масса; <
; e – заряд электрона, m – его масса; < 
 > – средняя длина свободного пробега электрона; < v > =
> – средняя длина свободного пробега электрона; < v > =  (18)
(18) Дж/К - постоянная Больцмана. С учетом (18) из (17) следует, что
Дж/К - постоянная Больцмана. С учетом (18) из (17) следует, что  , а
, а  , тогда как опыт показывает, что
, тогда как опыт показывает, что 


