
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные и затухающие колебания в контуре. Вынужденные электрические колебанияСодержание книги
Поиск на нашем сайте
Колебательным контуром называется замкнутая цепь, содержащая катушку индуктивности с индуктивностью L и конденсатор с емкостью С. Если в цепи нет активного сопротивления R (резистора), то в контуре возможны гармонические (незатухающие) колебания тока I, заряда конденсатора q и напряжения на элементах. Напряжение на конденсаторе: ЭДС самоиндукции в катушке НАПРЯЖЕНИЕ НА РЕЗИСТОРЕ ОПРЕДЕЛЕНИЕ ТОКА ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных незатухающих колебаний
Период Т = 2p Его решение q(t) = qv cos(w0 t + a), где a - начальная фаза. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных затухающих колебаний
Его решение q(t) = qv0 е-bt cos(wt + a), где логарифмическим декрементном затухания –
ДОБРОТНОСТЬ контура равна Q = Рассмотрим электромагнитный колебательный контур, в котором помимо ёмкости, индуктивности, сопротивления есть ещё и генератор переменного напряжения, то есть источник электрической энергии. Очевидно, что в таком контуре со временем (это время обычно мало) установятся вынужденные колебания тока с частотой генератора и с постоянной амплитудой; подвод энергии от генератора будет в точности компенсировать потери энергии на сопротивлении. Дифференциальное уравнение вынужденных колебаний заряда в электромагнитном контуре в стандартном (каноническом) виде получается следующим:
Вихревое электрическое поле Если провод неподвижен, а магнитное поле переменное, то в пространстве (в проводнике, в частности) возникает особое электрическое поле, называемое вихревым электрическим полем. Оно было открыто теоретически Максвеллом. Вихревое электрическое поле отличается от электростатического (потенциального) следующими свойствами: источником поля служат не заряды, а магнитное поле; в вихревом электрическом поле силовые линии – замкнутые, а работа по перемещению заряда по замкнутой линии не равна нулю. Рассмотрим подробнее вихревое электрическое поле на следующем примере. Пусть однородное переменное магнитное поле с индукцией B (t) создается внутри длинного соленоида С, по проводам которого протекает переменный ток. В этом поле находится неподвижное проволочное кольцо К радиусом r и площадью S. Линии магнитной индукции направлены вдоль оси соленоида и перпендикулярны плоскости кольца. Согласно, в кольце возникает ЭДС индукции.
Вследствие осевой симметрии, замкнутые линии напряженности вихревого электрического поля представляют собой окружности. Вектор E направлен по касательной к окружности, а его модуль E постоянен на данной окружности. На заряд q в кольце действует сила q E, которая при перемещении заряда по кольцу длиной L совершает стороннюю работу.
Следовательно, ЭДС в кольце равна произведению напряженности вихревого электрического поля на длину кольца Если ток в соленоиде изменяется по гармоническому закону с циклической частотой ω (ω = 2πν = 2π/T), то и магнитная индукция будет изменяться с такой же частотой где Bm – максимальное значение (амплитуда). Тогда dB/dt = ωBm cos ωt. Для нахождения напряженности вихревого электрического поля на расстоянии r от оси соленоида подставим в L =2πr и S = πr2, тогда Напряженность вихревого электрического поля пропорциональна частоте тока. Она может достигать больших значений в магнитных полях, создаваемых токами высокой частоты радиодиапазона.
28. ТОК СМЕЩЕ́НИЯ
В соответствии с теорией Максвелла, в цепи переменного тока, содержащей конденсатор, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, какое создавал бы ток, (названный током смещения), если бы он протекал между обкладками конденсатора. Из этого определения следует, что JD = J (т. е., численные значения плотности тока проводимости и плотности тока смещения равны), и, следовательно, линии плотности тока проводимости внутри проводника непрерывно переходят в линии плотности тока смещения между обкладками конденсатора. Плотность тока смещения jсм характеризует скорость изменения электрической индукции D во времени:
Ток смещения не выделяет джоулевой теплоты, его основное физическое свойство — способность создавать в окружающем пространстве магнитное поле. Вихревое магнитное поле создается полным током, плотность которого j, равна сумме плотности тока проводимости и тока смещения. Именно поэтому для этой величины и было введено название ток.
Уравнения Максвелла Уравнения Максвелла - уравнения классической электродинамики, описывающие динамику электромагнитного поля и его связь с зарядами и токами. Уравнения Максвелла явились теоретическим обобщением экспериментальных законов: Кулона, Ампера, законов электромагнитной индукции и других. Уравнения Максвелла в гауссовой системе единиц имеют вид
где E - напряжённость электрического поля, H - напряжённость магнитного поля, D - электрическая индукция, B - магнитная индукция, ρ - плотность электрического заряда, j - плотность электрического тока. Для того, чтобы использовать уравнения Максвелла для решения задач электродинамики в различных средах, необходимо учесть индивидуальные свойства среды. D = εE, B = μH, ε - диэлектрическая проницаемость среды, μ - магнитная проницаемость среды, σ - электропроводность среды. В вакууме без зарядов и токов D = ε0E, B = μ0H, div E = 0, div H = 0,
Эта система дифференциальных уравнений имеет решение - гармоническую плоскую волну. Векторы электрического и магнитного полей перпендикулярны направлению распространения волны и друг другу и находятся в фазе. Волна распространяется со скоростью. c = (μ0ε0)-1/2.
c - скорость света в вакууме, c = 2.99792458·108 м/с, ε0 - электрическая постоянная, ε0 = 8.85418782·10-12 Ф/м, μ0 - магнитная постоянная, μ0 = 1.25663706·10-6 Гн/м.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 205; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.231.197 (0.008 с.) |



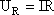
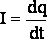
 где w0 =
где w0 =  - собственная частота контура.
- собственная частота контура.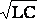
 , где b =
, где b =  - коэффициент затухания.
- коэффициент затухания.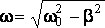 - частота затухающих колебаний.
- частота затухающих колебаний.

 или
или 


 =>
=> 


 представляет амплитуду электрического поля.
представляет амплитуду электрического поля. является основным уравнением Максвелла и выражает важнейшее свойство электромагнитного поля: в переменном магнитном поле возникает вихревое электрическое поле.
является основным уравнением Максвелла и выражает важнейшее свойство электромагнитного поля: в переменном магнитном поле возникает вихревое электрическое поле.


 div B = 0,
div B = 0, div D = 4πρ,
div D = 4πρ,





