
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поля соленоида, торой да, прямолинейного тока.Содержание книги
Поиск на нашем сайте
Найдем с помощью теоремы о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, который имеет N витков, и по которому течет ток (рис. 1). Будем считать длину соленоида во много раз больше, чем диаметр его витков. Экспериментальное изучение магнитного поля соленоида (см. главу "магнитное поле и его характеристики") показывает, что внутри соленоида поле однородно, вне соленоида — неоднородно и практически отсутствует. На рис. 1 даны линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем магнитная индукция вне его меньше. Поэтому приближенно можно полагать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а поле соленоида можно не учитывать. Для вычисления магнитной индукции В выберем замкнутый прямоугольный контур ABCDA, как показано на рис. 1. Циркуляция вектора В по замкнутому контуру ABCDA, который охватывает все N витков, используя формулу циркуляции вектора В, будет
Интеграл по ABCDA можно разложить на четыре интеграла: по АВ, ВС, CD и DA. На участках АВ и CD контур и линии магнитной индукции перпендикулярны: Bl=0. На участке вне соленоида B=0. На участке DA циркуляция вектора В равна Вl (контур и линии магнитной индукции совпадают); значит,
Из (1) приходим к формуле магнитной индукции поля внутри соленоида (в вакууме):
Мы видим, что поле внутри соленоида однородно (при расчетах пренебрегают краевыми эффектами в областях, прилегающих к торцам соленоида). Но отметим, что вывод этой формулы не совсем корректен (поскольку линии магнитной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно найти поле внутри соленоида можно, используя закон Био — Савара — Лапласа; в результате получается такая же формула (2). Важное практическое значение имеет также магнитное поле тороида — кольцевой катушки, у которой витки намотаны на сердечник, который имеет форму тора (рис. 2). Магнитное поле, как известно из опыта, сосредоточено внутри тороида, а вне его поле равно нулю. В данном случае линии магнитной индукции, как следует из соображений симметрии, есть окружности, у которых центры расположены по оси тороида. В качестве контура возьмем одну такую окружность радиуса r. Тогда, используя теорему о циркуляции, B•2πr=μ0NI, откуда следует, что магнитная индукция внутри тороида (в вакууме)
где N — число витков тороида Если контур проходит вне тороида, то токов он не охватывает и B•2πr = 0. Следовательно, что поле вне тороида отсутствует (что показывает и опыт). Прямолинейный ток: Магнитное поле прямолинейного тока рассмотрим на примере (см. рисунок). Имеется проводник с токм. Рассмотрим контур в виде окружности с радиусом r, эта окружность совпадает с силовой линией магнитного поля проводника с током I. В каждой точке нашего контура напряженность магнитного поля одинакова. Магнитодвижущая сила F вдоль контура по закону полного тока: F = Σ I = Σ Hr * ΔL Напряженность Hr выносим за знак суммирования, т.к. она одинакова для всех точек контура, а ΣΔL равна длине окружности радиуса r: F = Σ I = Hr * 2πr Полный ток Σ I равен алгебраической сумме токов, проходящих через поверхность, ограниченную контуром r. В нашем случае это только ток I: I = Σ I = Hr * 2πr Отсюда получаем напряженность магнитного поля в любой точке нашего контура: Hr = I/(2πr) Вот эта формула и описывает магнитное поле прямолинейного тока. Правда она справедлива только для проводника, длина которого много больше радиуса контура r. Если же длина проводника и радиус контура, на котором мы исследуем магнитное поле прямолинейного тока, близки по величине, то для определения напряженности магнитного поля используют формулу, вытекающую из закона Био-Савара: HA = I(cosα + cosβ)/(4πr) Точку А, находящуюся на контуре радиуса r, соединяем линиями с концами проводника, получаем углы α и β. Если удлинять проводник или приближать точку А к проводнику, то углы α и β будут стремиться к нулю, а выражение (cosα + cosβ) будет стремиться к двум, ведь косинус нуля равен единице. Тогда получаем: HA = I(cosα + cosβ)/(4πr) ~= I(2)/(4πr) = I/(2πr) т.е. переходим к формуле напряженности магнитного поля проводника бесконечной длины.
Сила Лоренца. Сила Ампера. Сила ампера: Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположном — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила
Элементарную силу взаимодействия
Сила Лоренца: Выражение для силы, с которой магнитное поле действует на движущийся заряд, впервые получил голландский физик Хендрик Антон Лоренц (1895 г.). В его честь эта сила называется силой Лоренца. Сила Лоренца — это сила, с которой магнитное поле действует на движущуюся в нем заряженную частицу.
Модуль силы Лоренца равен произведению модуля индукции магнитного поля B(вектор), в котором находится заряженная частица, модуля заряда q этой частицы, ее скорости υ и синуса угла между направлениями скорости и вектора индукции магнитного поля
Для определения направления силы Лоренца применяют правило левой руки: если левую руку расположить так, чтобы вектор индукции магнитного поля ( Поскольку величина B∙sin α представляет собой модуль компоненты вектора индукции, перпендикулярной скорости заряженной частицы,
Так как сила Лоренца перпендикулярна вектору скорости частицы, то она не может изменить значение скорости, а изменяет только ее направление и, следовательно, не совершает работы.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 174; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.239.70 (0.008 с.) |





 , с которой магнитное поле действует на элемент объёма dV проводника с током плотности
, с которой магнитное поле действует на элемент объёма dV проводника с током плотности  , находящегося в магнитном поле с индукцией
, находящегося в магнитном поле с индукцией  :
:
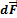 между элементами
между элементами  и
и  проводников, по которым протекают токи I 1 и I 2 можно определить из закона Ампера:
проводников, по которым протекают токи I 1 и I 2 можно определить из закона Ампера:

 ) входил в ладонь, четыре вытянутых пальца указывали направления скорости движения положительно заряженной частицы (
) входил в ладонь, четыре вытянутых пальца указывали направления скорости движения положительно заряженной частицы ( ), тогда отогнутый на 90° большой палец укажет направление силы Лоренца (
), тогда отогнутый на 90° большой палец укажет направление силы Лоренца ( ) (рис. 3, а). Для отрицательной частицы четыре вытянутых пальца направляют против скорости движения частицы (рис. 3, б).
) (рис. 3, а). Для отрицательной частицы четыре вытянутых пальца направляют против скорости движения частицы (рис. 3, б). , то ориентацию ладони можно определять именно этой компонентой — перпендикулярная составляющая к скорости заряженной частицы должна входить в открытую ладонь левой руки.
, то ориентацию ладони можно определять именно этой компонентой — перпендикулярная составляющая к скорости заряженной частицы должна входить в открытую ладонь левой руки.


