
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кондуктивный теплообмен в плоской стенкеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ПРЕДИСЛОВИЕ
«Гидравлика и теплотехника» является базовой общеинженерной дисциплиной для студентов, обучающихся по направлению «Защита окружающей среды». Она состоит из двух частей: - теоретические основы технологических процессов; - типовые процессы и аппараты промышленной технологии. Вторая часть включает три основных раздела: - гидродинамика и гидродинамические процессы; - тепловые процессы и аппараты; - массообменные процессы и аппараты. По первой части дисциплины были опубликованы конспекты лекций Н.Х. Зиннатуллина, А.И. Гурьянова, В.К. Ильина (Гидравлика В данном пособии излагается второй раздел второй части. В этом разделе будут рассмотрены наиболее распространенные случаи кондуктивного и конвективного теплообмена, промышленные способы передачи тепла, выпаривание, а также принцип работы и конструкции теплообменной аппаратуры. Учебное пособие состоит из трех глав, каждая из них заканчивается вопросами, которые студенты могут использовать для самоконтроля. Основная задача представленного учебного пособия – научить студентов проводить инженерные расчеты тепловых процессов и подбор необходимой аппаратуры для их проведения.
ЧАСТЬ. 1. ТЕПЛООБМЕН
Промышленные технологические процессы протекают в заданном направлении только при определенных температурах, которые создаются путем подвода или отвода тепловой энергии (теплоты). Процессы, скорость протекания которых зависит от скорости подвода или отвода теплоты, называются тепловыми. Движущей силой тепловых процессов является разность температур между фазами. Аппараты, в которых осуществляются тепловые процессы, называются теплообменниками, в них тепло переносится теплоносителями. Расчет теплообменных процессов сводится обычно к определению межфазной поверхности теплообмена. Эта поверхность находится
Конвективный теплообмен
При конвекции перенос теплоты происходит макрообъемными частицами потока теплоносителя. Конвекция всегда сопровождается теплопроводностью. Как известно, теплопроводность – явление молекулярное, конвекция – явление макроскопическое, при котором Конвективный перенос теплоты описывается уравнением Фурье-Кирхгофа. Закономерности течения среды описываются уравнениями Навье-Стокса (ламинарный режим) и Рейнольдса (турбулентный режим), а также уравнением неразрывности. Исследование закономерностей конвективного теплообмена можно провести в изотермической и неизотермической постановке. В изотермической постановке сначала решаются уравнения Навье-Стокса и неразрывности, затем полученные значения скоростей используются для решения уравнения Фурье-Кирхгофа. Полученные таким способом значения коэффициентов теплоотдачи впоследствии уточняются, корректируются. В неизотермической постановке уравнения Навье-Стокса, неразрывности и Фурье-Кирхгофа решаются совместно, с учетом зависимости теплофизических свойств среды от температуры. В последнее время разработаны методы решения многих задач теплоотдачи в ламинарных потоках жидкости с учетом зависимости вязкости жидкости от температуры. Для турбулентных течений все сложнее. Однако можно использовать приближенные численные решения с помощью компьютерных технологий.
Для решения этих уравнений необходимо поставить условия однозначности, которые включают начальные и граничные условия. Граничные условия теплообмена могут быть заданы различным способом: - граничные условия первого рода – задаются распределением температуры стенки:
простейший случай, когда Т cт = const; - граничные условия второго рода – задается распределение теплового потока на стенке
- граничные условия третьего рода – задается распределение температуры среды, окружающей канал и коэффициент теплоотдачи
Выбор вида граничного условия зависит от условий работы теплообменного оборудования.
На плоской пластине
Рассмотрим поток, обладающий неизменными теплофизическими характеристиками (r, m, l, cp = const), совершающий вынужденное движение вдоль плоской полубесконечной тонкой пластины и обменивающейся с ней теплом. Предположим, что неограниченный поток со скоростью Выделим гидродинамический и тепловой пограничные слои Проанализируем уравнения неразрывности и Навье-Стокса. Задача двухмерная, поскольку wz,
Как известно «х» dг, поэтому Следовательно, имеем
Записывать аналогичные уравнения для оси у не имеет смысла, так как wy может быть найдена из уравнения неразрывности (22). Используя аналогичные процедуры можно упростить и уравнение Фурье-Кирхгофа
Система дифференциальных уравнений (22)–(24) составляет изотермическую математическую модель плоского стационарного теплового ламинарного пограничного слоя. Сформулируем граничные условия Итак, граничные условия:
w x (x, 0) = 0, x > 0; wx (x, ∞) = T (x, 0) = T ст, x > 0; T (x, ∞) = T °; T (0, y) = T °. (26)
Точное решение этой задачи в виде бесконечных рядов было получено Блазиусом. Имеются более простые приближенные решения: метод интегральных соотношений (Юдаев) и теорема импульсов (Шлихтинг). А.И. Разиновым задача была решена методом сопряженного физического
Pr = ν/a.
Коэффициент А в формуле (27) у Разинова – 5,83; Юдаева – 4,64; Блаузиуса – 4; Шлихтинга – 5,0. Примерный вид найденных зависимостей приведен на рис. 1.3. Как известно, для газов Pr ≈ 1, капельных жидкостей Pr > 1. Полученные результаты позволяют определить коэффициенты импульса и теплоотдачи. Локальные значения γ(x) и Nu г, x
Рис. 1.3. Гидродинамический и тепловой ламинарные пограничные слои
на плоской пластине
Усредненные значения
Аналогично для теплоотдачи
В данном случае аналогия тепло- и импульсоотдачи сохраняется (исходные уравнения одинаковы, граничные условия подобны). Критерий, характеризующий гидродинамическую аналогию процесса теплоотдачи имеет вид
Pт-г, x = Nu т, x / Nu г, x = Pr 1/3. (33)
Если Pr = 1, то Pт-г, x = 1, следовательно полная аналогия процессов импульсо- и теплоотдачи. Из полученных уравнений следует
γ ~
Как правило, подобная качественная зависимость выполняется Задача рассматривается в изотермической постановке, тепловые граничные условия первого рода Т ст = const. По мере удаления от кромки пластины (увеличения координаты х) происходит рост dг(х). При этом неоднородность поля скорости wx распространяется в области все более удаленные от границы раздела фаз, Толщина же всего турбулентного теплового пограничного слоя обычно определяется из условия ν т = ат, следовательно dг = dт. Сначала рассмотрим турбулентный гидродинамический пограничный слой (рис. 1.4). Оставим в силе все приближения, сделанные для ламинарного слоя. Единственное отличие – наличие νт (у), поэтому
Сохраним и граничные условия. Решением системы уравнений (35)
Рис. 1.4. Гидродинамический и тепловой турбулентные пограничные слои на плоской пластине
Как и в случае ламинарного пограничного слоя возможно использование осредненных по длине l коэффициентов импульсоотдачи
Рассмотрим тепловой турбулентный пограничный слой. Уравнение энергии имеет вид
Если Pr > 1, то внутри вязкого подслоя можно выделить тепловой подслой, где молекулярный перенос тепла
Для локального коэффициента теплоотдачи решение математической модели имеет вид
Среднее по длине пластины значение
Ниже представлены образование турбулентного пограничного слоя (а) и распределение локального коэффициента теплоотдачи (б) при продольном обтекании плоской полубесконечной пластины (рис. 1.5).
Рис. 1.5. Пограничные слои dг и dт и локальный коэффициент теплоотдачи a на плоской пластине
В ламинарном слое (х ≤ l кр) тепловой поток только за счет теплопроводности, для качественной оценки можно использовать соотношение a ~ В переходной зоне общая толщина пограничного слоя увеличивается. Однако значение a при этом увеличивается, потому что толщина ламинарного подслоя уменьшается, а в образующемся турбулентном слое тепло переносится не только теплопроводностью, но и конвекцией вместе Итак, рассмотрены гидродинамический и тепловой пограничные слои на плоской пластине. Качественный характер полученных зависимостей справедлив и для пограничных слоев, образующихся при обтекании более сложных поверхностей.
Теплообмен в круглой трубе
Рассмотрим стационарный теплообмен между стенками горизонтальной прямой трубы круглого сечения и потоком, обладающим неизменными теплофизическими характеристиками и движущимся за счет вынужденной конвекции внутри нее. Примем тепловые граничные условия первого рода, т.е. Т ст = const. I. Участки гидродинамической и термической стабилизации. При входе жидкости в трубу за счет торможения, вызываемого стенками, на них формируется гидродинамический пограничный слой. Подобно изменению профиля скоростей по длине трубы изменяется II. Рассмотрим ламинарное движение жидкости.
Ранее, в разделе дисциплины «Гидродинамика и гидродинамические процессы» [2], нами был рассмотрен гидродинамический начальный участок. Для определения длины начального участка была предложена следующая зависимость
Для жидкости Pr > 1, следовательно, тепловой пограничный слой будет находиться внутри гидродинамического пограничного слоя. Температура жидкости во входном сечении теплообменного участка постоянна по сечению и равна Т ° и в ядре потока она не меняется. При этих условиях уравнение теплового пограничного слоя имеет вид
Решение этого уравнения при вышеперечисленных условиях дает: · для длины теплового начального участка
· для местного коэффициента теплоотдачи
· для среднего коэффициента теплоотдачи длиной
· для местного числа Нуссельта
· для среднего числа Нуссельта
Рассмотрим уравнение (42). Если
Рис. 1.6. Профиль температуры на начальном и стабилизированном участке при ламинарном течении жидкости в цилиндрической трубе
При турбулентном течении потока в трубе, как и на плоской пластине, во-первых, толщины гидродинамического и теплового пограничных слоев совпадают; а во-вторых, растут значительно быстрее, чем для ламинарных. Это приводит к уменьшению длины участков термической
III. Стабилизированный теплообмен при ламинарном движении среды. Рассмотрим стационарный теплообмен в круглой трубе, когда теплофизические свойства жидкости постоянны (изотермический случай), профиль скорости не меняется по длине, температура стенки трубы постоянна и равна Т ст, в потоке отсутствуют внутренние источники тепла,
Граничные условия:
Решение этой задачи впервые было получено Гретцем, затем Нуссельтом, в виде суммы бесконечного ряда. Несколько иное решение было получено Шумиловым и Яблонским. Полученное решение справедливо Для области стабилизированного теплообмена локальный коэффициент теплоотдачи равен предельному
Как видно из рисунка (рис. 1.7), с увеличением
Рис. 1.7. Изменение местного IV. Стабилизированный теплообмен при турбулентном движении среды. Исходное уравнение
Граничные условия:
При решении задачи возникает проблема выбора профиля скорости wx. Одни для wx используют логарифмический закон (А.И. Разинов), другие – закон 1/7 (В.Б. Коган). Отмечается консервативность турбулентных течений, которая заключается в слабом влиянии граничных условий и поля скорости wx на коэффициенты теплоотдачи. Для числа Нуссельта предлагается следующая формула
Как и для ламинарного движения в области стабилизированного теплообмена при турбулентном течении среды Nu не зависит от координаты х. Нами был рассмотрены выше частные случаи теплообмена, а именно: при изотермической постановке задачи и тепловых граничных условиях первого рода теплообмен в гладких цилиндрических трубах и плоских горизонтальных пластинах. В литературе имеются решения тепловых задач и для других случаев. Отметим, что шероховатость поверхности трубы и пластины ведет
Подвод теплоты
Для решения этой задачи применяют различные теплоносители. 1. По назначению: - греющий ТН; - охлаждающий ТН, хладаноситель; - промежуточный ТН; - сушильный агент. 2. По агрегатному состоянию: · Однофазные: - низкотемпературная плазма; - газы; - неконденсирующиеся пары; - не кипящие и неиспаряющиеся при данном давлении жидкости; - растворы; - зернистые материалы. · Много-, двухфазные: - кипящие, испаряющиеся и распыляемые газом жидкости; - конденсирующиеся пары; - плавящиеся, затвердевающие материалы; - пены, газовзвеси; - аэрозоли; - эмульсии, суспензии и т.д. 3. По диапазону температур и давления: - высокотемпературные ТН (дымовые, топочные газы, расплавы солей, жидкие металлы); - среднетемпературные ТН (водяной пар, вода, воздух); - низкотемпературные ТН (при атмосферном давлении T кип ≤ 0 °C); криогенные(сжиженные газы – кислород, водород, азот, воздух и др.). С увеличением давления растет и температура кипения жидкостей. В качестве прямых источников тепловой энергии на промышленных предприятиях используют топочные (дымовые) газы и электроэнергию. Вещества, передающие от этих источников теплоту, в ТО называют промежуточными ТН. Наиболее распространенные промежуточные ТН: - водяной пар насыщенный; - горячая вода; - перегретая вода; - органические жидкости и их пары; - минеральные масла, жидкие металлы. Требования к ТН: - большая r, ср; - высокое значение теплоты парообразования; - низкая вязкость; - негорючесть, нетоксичность, термостойкость; - дешевизна.
Отвод теплоты
Многие процессы промышленной технологии протекают в условиях, когда возникает необходимость отвода теплоты, например, при охлаждении газов, жидкостей или при конденсации паров. Рассмотрим некоторые способы охлаждения. Охлаждение водой и низкотемпературными жидкими хладагентами. Охлаждение водой используют для охлаждения среды до 10–30 °С. Речная, прудовая и озерная вода в зависимости от времени года имеет температуру 4–25 °С, артезианская – 8–12 °С, а оборотная (летом) – около 30 °С. Расход охлаждающей воды
Здесь Достижение более низких температур охлаждения можно обеспечить Охлаждение воздухом. Наиболее широко воздух в качестве охлаждающего агента используют в смесительных теплообменниках – градирнях, являющихся основным элементом оборудования водооборотного цикла (рис. 2.5).
Рис. 2.5. Градирни с естественной (а) и принудительной (б) тягой
Горячая вода в градирне охлаждается как за счет контакта с холодным воздухом, так и в результате так называемого испарительного охлаждения,
Смесительные теплообменники
В смесительных теплообменниках (СТО) передача тепла от одного теплоносителя к другому происходит при их непосредственном соприкосновении или смешении, следовательно, термическое сопротивление стенки (разделяющей теплоносители) отсутствует. Наиболее часто СТО применяют для конденсации паров, нагревания и охлаждения воды и паров. По принципу устройства СТО подразделяют на барботажные, полочные, насадочные и полые (с разбрызгиванием жидкости) (рис. 2.18).
Рис. 2.18. Схемы СТО: а) барботажный смесительный теплообменник для нагрева воды; б) насадочный теплообменник-конденсатор; в) полочный барометрический конденсатор; г) полый ЧАСТЬ 3. ВЫПАРИВАНИЕ
Выпаривание – процесс концентрирования растворов твердых нелетучих веществ путем удаления летучего растворителя в виде паров. Выпаривание обычно проводится при кипении. Обычно из раствора удаляется только часть растворителя, так как вещество должно оставаться Существует три метода выпаривания: - поверхностное выпаривание осуществляется путем нагревания раствора на теплообменной поверхности за счет подвода тепла к раствору через стенку от греющего пара; - адиабатическое выпаривание, которое происходит путем мгновенного испарения раствора в камере, где давление ниже, чем давление насыщенного пара; - выпаривание путем контактного испарения - нагревание раствора осуществляется при прямом контакте между движущимся раствором В промышленной технологии в основном применяется первый метод выпаривания. Далее о первом методе. Для осуществления процесса выпаривания необходимо теплоту от теплоносителя передать кипящему раствору, что возможно лишь при наличии разности температур между ними. Разность температур между теплоносителем и кипящим раствором называют полезной разностью температур. В качестве теплоносителя в выпарных аппаратах применяется насыщенный водяной пар (греющий или первичный). Выпаривание – типичный теплообменный процесс – перенос теплоты за счет конденсации насыщенного водяного пара к кипящему раствору. В отличие от обычных теплообменников выпарные аппараты состоят из двух основных узлов: греющей камеры или кипятильника и сепаратора. Сепаратор предназначен для улавливания капель раствора из пара, который образуется при кипении. Этот пар называется вторичным или соковым. Температура вторичного пара всегда меньше температуры кипения раствора. Для поддержания постоянного вакуума в конденсаторе необходимо отсасывать парогазовую смесь вакуум-насосом. В зависимости от давления вторичного пара различают выпаривание при р атм, р изб, р вак. В случае выпаривания при р вак снижается температура кипения раствора, при p изб – вторичный пар используется в технологических целях. Температура кипения раствора всегда выше температуры кипения чистого растворителя. Например, для насыщенного водного раствора Температурные потери
Обычно в однокорпусных выпарных установках известны давления греющего и вторичного паров, т.е. их температуры. Разность между температурами греющего и вторичного паров называют общей разностью температур выпарных аппаратов
Общая разность температур
Здесь D¢ - концентрационная температурная депрессия; D¢¢ - гидростатическая температурная депрессия; D¢ определяют как разницу температур кипения раствора Т кип. р и чистого растворителя Т кип. чр при p = = const
D¢ = Т кип. р – Т кип. чр, Т кип. чр, D¢ = Т кип. р - T вп. (98)
Температура образующегося при кипении раствора вторичных паров ниже, чем температура кипения самого раствора, т.е. часть температур теряется бесполезно; D¢¢ характеризует повышение температуры кипения раствора с увеличением гидростатического давления. Обычно по высоте кипятильных труб определяют среднее давление, и для этого давления определяют среднюю температуру кипения растворителя Т ср.
Здесь p a - давление в аппарате; rпж - плотность парожидкостной смеси
D² = T ср - T вп, (99)
где T ср - температура кипения растворителя при p = p ср; T вп - температура вторичного пара при давлении p а.
Многокорпусное выпаривание
В многокорпусной выпарной установке вторичный пар (рис. 3.2, 3.3) предыдущего корпуса используется в качестве греющего пара Уравнения материальных балансов позволяют определить количество испаренной воды в установке и к
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 905; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.151.11 (0.016 с.) |

 l(Т)
l(Т) ; (19)
; (19) ; (20)
; (20) . (21)
. (21)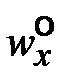
 и Т ° постоянны.
и Т ° постоянны. . По экспериментальным данным известно, что в гидродинамическом пограничном слое
. По экспериментальным данным известно, что в гидродинамическом пограничном слое  . В ядре потока
. В ядре потока  const, поэтому, согласно уравнению Бернулли
const, поэтому, согласно уравнению Бернулли 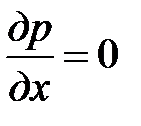 , в пограничном слое то же самое
, в пограничном слое то же самое .
. .
. ; (22)
; (22) . (23)
. (23) . (24)
. (24) . Для поля температуры аналогичные рассуждения.
. Для поля температуры аналогичные рассуждения. ; wx (0, y) =
; wx (0, y) =  ; (27)
; (27)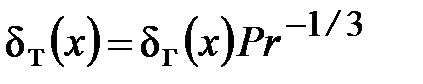 , Pr ≥ 1; (28)
, Pr ≥ 1; (28) ,
, 
 . (29)
. (29)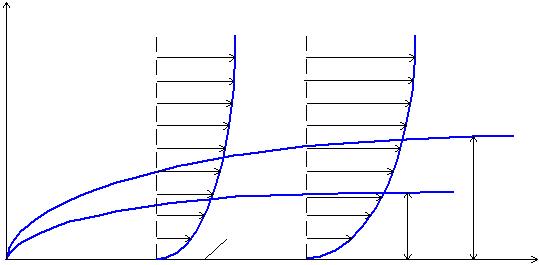

 и
и  по участку длиной l
по участку длиной l ,
, 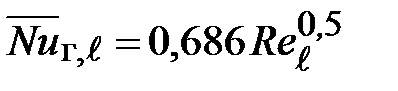 ,
,  . (30)
. (30) ,
,  ; (31)
; (31) ,
,  . (32)
. (32) , m; a ~
, m; a ~  . (35)
. (35)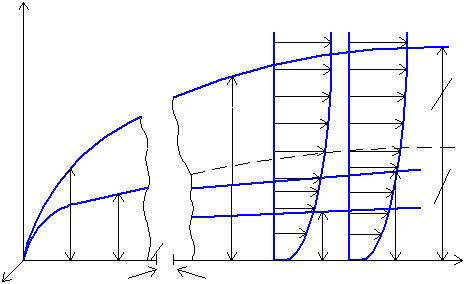


 . (36)
. (36) . (37)
. (37) . (38)
. (38) . (39)
. (39) определяется так
определяется так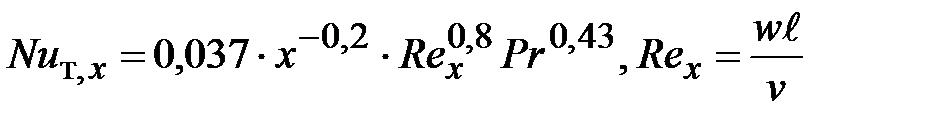 . (40)
. (40)

 .
. .
. .
. . (41)
. (41) ; (42)
; (42) ; (43)
; (43)
 ; (44)
; (44) ; (45)
; (45)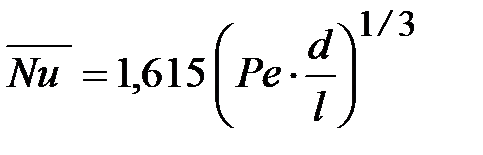 . (46)
. (46) , то
, то  .
. . (47)
. (47)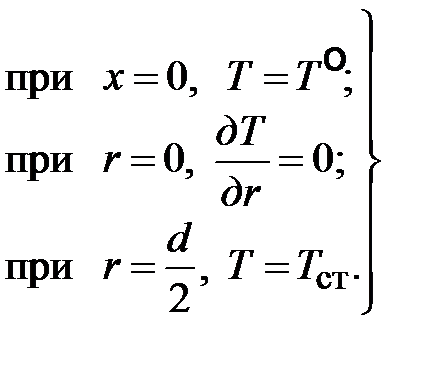 (48)
(48) или
или  (49)
(49) число Nu уменьшается, асимптотически приближаясь на втором участке кривой
число Nu уменьшается, асимптотически приближаясь на втором участке кривой

 и среднего Nu по длине круглой трубы при Т ст = const
и среднего Nu по длине круглой трубы при Т ст = const . (50)
. (50) (51)
(51)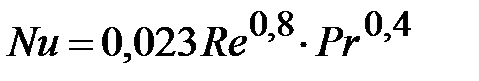 . (52)
. (52)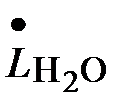 определяют из уравнения теплового баланса
определяют из уравнения теплового баланса . (83)
. (83) – расход охлаждаемого теплоносителя; Н н и Н к – начальная
– расход охлаждаемого теплоносителя; Н н и Н к – начальная – потери в окружающую среду.
– потери в окружающую среду.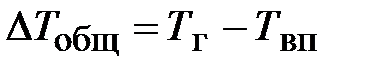 . (96)
. (96)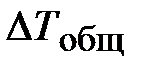 связана с полезной разностью температур
связана с полезной разностью температур 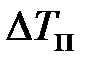 соотношением
соотношением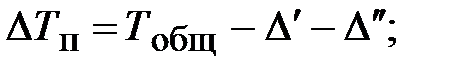
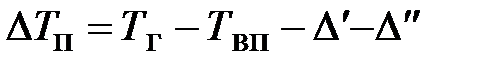 . (97)
. (97)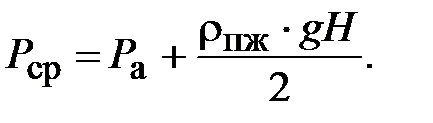
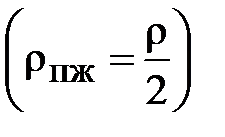 ; H - высота кипятильных труб.
; H - высота кипятильных труб.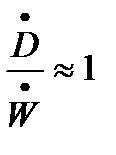 по всем корпусам, то общий расход греющего пара на процесс уменьшается пропорционально числу корпусов. Практически, в реальных условиях такое соотношение не выдерживается, оно, как правило, выше. Далее рассмотрим уравнения материальных и тепловых балансов для многокорпусной выпарной установки (см. рис. 3.2), которые представляют собой систему уравнений, записанных для каждого корпуса в отдельности.
по всем корпусам, то общий расход греющего пара на процесс уменьшается пропорционально числу корпусов. Практически, в реальных условиях такое соотношение не выдерживается, оно, как правило, выше. Далее рассмотрим уравнения материальных и тепловых балансов для многокорпусной выпарной установки (см. рис. 3.2), которые представляют собой систему уравнений, записанных для каждого корпуса в отдельности.


