
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конвективный теплообмен в турбулентном пограничном слоеСодержание книги
Поиск на нашем сайте
Для простоты изложения ограничимся рассмотрением пограничного слоя, образуемого при движении жидкости вдоль плоской поверхности. Этот случай показан на рис.7.1.
Рис. 7.1. Образование пограничного слоя вблизи плоской поверхности: W0 и T0 – скорость и температура набегающего потока жидкости;
расстоянии "х" от начала пластины
Пограничный слой разделяют на динамический и тепловой. В пределах динамического слоя сильно изменяется скорость потока. За пределами динамического слоя скорость равна скорости основного (набегающего) потока – W0. Для определенности границей пограничного слоя считают условную поверхность, на которой соблюдается условие: Т» 0,99×T0 при Tст < T0; Т» 1,01×T0 при Tст > T0, где Tст – температура, жидкости на стенке (плоской поверхности). Таким образом, принимается, что на границе пограничного слоя значение температуры и скорости отличается от параметров основного потока не более чем на 1%. Закономерно возникает вопрос: для чего нужно понятие пограничного слоя и зачем рассчитывать скорости и температуры жидкости в пределах слоя? Дело в том, что задача конвективного теплообмена в реальных системах (печах) чаще всего сводится к определению тепловых потоков от жидкости к твердой стенке. Эти тепловые потоки зависят, главным образом, от распределения скоростей и температур в тонком слое, прилегающем к твердой стенке. Поэтому с достаточно высокой точностью можно перейти от решения полной, очень трудоемкой, задачи конвективного теплообмена в объеме печи к довольно простой задаче, конвективного теплообмена в пограничном слое. На практике наиболее близки к модельной задаче (рис.7.1) случаи, когда рассматривается теплообмен в плоском рекуператоре или теплообмен в нагревательной печи при движении продуктов горения вдоль плоской заготовки или вдоль стен печи. Пограничный слой описывается системой основных уравнений: а) уравнение движения; б) уравнение неразрывности (сплошности); в) уравнение энергии. Считаем, что скорость набегающего потока не зависит от времени, тогда уравнение движения представляет из себя упрощенное уравнение Навье-Стокса
где Wx и Wy – составляющие вектора скорости по осям х и у, n –коэффициент кинематической вязкости жидкости. Уравнение неразрывности представляет собой запись уравнения сохранения массы для несжимаемой жидкости
Система (7.1-7.2) называется уравнениями пограничного слоя Прандтля. Уравнение энергии в приближении пограничного слоя имеет вид, по форме напоминающий уравнение движения (7.1):
где Т - температура потока; а - коэффициент температуропроводности жидкости. Для получения однозначного решения системы (7.1-7.3) вводятся граничные условия: при y = 0: при при при х = 0: Wx = W0, Wy = 0, T = T0 (7.7)
Из полученной системы (7.1-7.7) необходимо найти Wx, Wy и T как функции координат х и у. Это будет, так сказать, исходной информацией для дальнейшего определения тепловых потоков, коэффициентов трения,коэффициентов теплоотдачи и т.д., которые мы рассматривать не будем, поскольку это не является целью данной работы. Мы будем рассматривать только методы определения полей скоростей и температуры в пределах пограничного слоя. За основу берем метод конечных разностей.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 433; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |


 и
и  – толщины динамического и теплового пограничных слоев на
– толщины динамического и теплового пограничных слоев на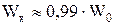 . Аналогично тепловой пограничный слой представляет из себя слой жидкости, в пределах которого сильному изменению уже подвержена температура. На границе теплового слоя выполняется условие:
. Аналогично тепловой пограничный слой представляет из себя слой жидкости, в пределах которого сильному изменению уже подвержена температура. На границе теплового слоя выполняется условие: (7.1)
(7.1) (7.2)
(7.2) (7.3)
(7.3) (7.4)
(7.4) :
:  (7.5)
(7.5) :
: 


