
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простейшие численные методы решения О.Д.У.Содержание книги
Поиск на нашем сайте
О.Д.У. можно решить многими методами. Не касаясь аналитических методов, применимых для ограниченного класса О.Д.У., отметим, что наиболее распространены следующие численные методы: метод Эйлера и метод Рунге-Кутта. Ограничимся рассмотрением метода Эйлера, имеющего 1-й порядок точности. Достоинство метода в наглядности и простоте реализации. Как и большинство численных методов, метод Эйлера основывается на разложении искомой функции (т.е. температуры) в ряд Тейлора. Если функция
где j – номер шага по времени; Теперь отбросим в уравнении (4.12) члены ряда 2-го порядка и выше в силу их малости по сравнению с членами ряда 1-го порядка (при достаточно малых
Для перехода к равенству вводим сеточную функцию приближенного решения –
В соответствии с (4.4) О.Д.У. в точке j имеет вид
Подставив (4.15) в (4.14), окончательно получим, так называемую, явную схему Эйлера:
Из этой формулы вытекает, что значение температуры на новом шаге по времени (j+1) вычисляется по значению температуры на текущем шаге. т.е. в явном виде. Отсюда и название схемы: явная. Пример 1. Найти закон изменения температуры стальной заготовки диаметром Д, нагреваемой конвекцией в печи, если температура печных газов изменяется по закону Исходные данные: Д = 2 R = 0,025 м; R = Д/2 = 0,0125 м; плотность – r = 8000 кг/м3; удельная теплоемкость – C = 600 Дж/(кг×К); коэффициент теплоотдачи – a = 30 Вт/(м2 К); коэффициент теплопроводности – l = 30 Вт/(м2×К); начальная температура – Т0 = 0 С. Решение. Проверим, является ли тело термически тонким. Для этого найдем критерий Био:
Т.к. Bi < 0,1, то тело можно отнести к термически тонким [1]. Процесс нагрева конвекцией термически тонкого тела описывается уравнением
где V и S – объем и площадь поверхности нагреваемого тела; Т – температура тела. Отсюда
где
Если раскроем выражение для
Для решения уравнения (4.17) относительно температуры нагреваемого тела Т используем явную схему Эйлера (4.16). Для этого сначала строим разностную сетку. Принимаем, допустим, 5 шагов по времени, т.е. N = 5. Тогда величина шага будет равна
В соответствии с обозначениями (4.16), имеем
где j = 1,2,..., N. Таким образом перешли от сеточной функции точного решения
Результаты расчета сводим в таблицу 4.1. В данном случае линейное изменение температуры печных газов но времени приводит к линейному увеличению температуры металла. Проверка. Подставим полученную зависимость температуры металла от времени Т = t (4.18)
в исходное уравнение (4.17). Получим
Это тождество показывает, что полученное численным методом решение (4.18) верно.
Таблица 4.1 Результаты численного решения задачи нагрева ТТТ
Приведенный пример показывает, как довольно просто можно найти численное решение любого обыкновенного дифференциального уравнения с использованием явной схемы Эйлера. Кроме явной схемы Эйлера существует неявная схема. Она выводится почти аналогично явной, но с небольшими особенностями. Первичное разложение функции температуры
Здесь, также как и в (4.12), j – номер шага по времени; Отсюда, пренебрегая членами ряда 2-го порядка и выше, а также переходя от сеточной функции точного решения
Выражение (4.20) отражает неявную схему Эйлера. Видно, что температура на (j+1)-м шаге по времени входит и в левую, и в правую часть уравнения (4.20) или, как говорят, получена в неявном виде. Для получения решения этого уравнения, в общем случае являющегося трансцендентным, надо использовать один из итерационных методов.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.108.134 (0.01 с.) |

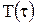 раскладывается в ряд в окрестности точки
раскладывается в ряд в окрестности точки 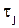 (см. рис. 4.1), то в точке разностной сетки
(см. рис. 4.1), то в точке разностной сетки 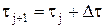 функция будет равна
функция будет равна , (4.12)
, (4.12) – величина шага по времени.
– величина шага по времени.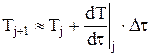 . (4.13)
. (4.13)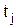 :
: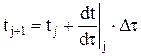 . (4.14)
. (4.14)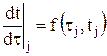 (4.15)
(4.15)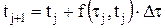 или
или 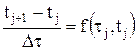 (4.16)
(4.16)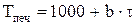 , °C, где
, °C, где 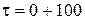 – время нагрева, с;
– время нагрева, с; 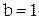 °С/с.
°С/с.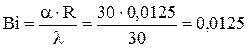 .
. ,
, ,
,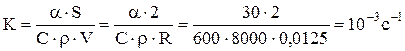 .
.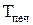 , то получим
, то получим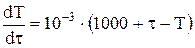 , (4.17)
, (4.17)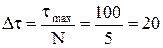 с,
с,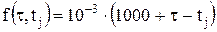 ,
,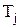 к сеточной функции приближенного решения
к сеточной функции приближенного решения 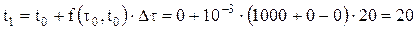 °С;
°С;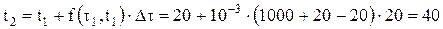 °С;
°С; °С;
°С; °С;
°С;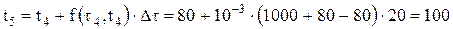 °С.
°С.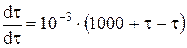 или 1 º 1.
или 1 º 1.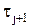 . В этом случае в точке
. В этом случае в точке 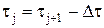 функция будет иметь вид
функция будет иметь вид (4.19)
(4.19) или
или 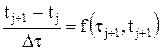 . (4.20)
. (4.20)


