
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зональный метод расчета стационарного теплообмена в системе тел с диатермичной средойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для определенности рассмотрим двумерную замкнутую систему тел (печь), как показано на рис. 9.1. Разобьем профиль печи на N зон, в пределах которых температуры, тепловые потоки и степени черноты считаем заданными (прямая задача). Требуется рассчитать результирующие тепловые потоки по зонам.
Рис. 9.1. Замкнутая геометрическая система тел
Для избегания путаницы в названиях различных видов тепловых потоков дадим их определение для i-й зоны [15]: 1. Поток собственного излучения
где 2. Поток отраженного излучения
где 3. Поток поглощенного излучения
4. Поток эффективного (исходящего [13]) излучения
5. Поток результирующего излучения
или
Основное отличие классического зонального метода от подобных методов в том, что он оперирует эффективными потоками и для его реализации больше подходит выражение (9.6) для расчета результирующих потоков. Основная задача: как связать
где В этом случае
и
Здесь Проанализируем выражение (9.9). Для определения
или
Если уравнение (9.11) записать N раз, т.е. для каждой зоны, то получим систему из N линейных алгебраических уравнения относительно N неизвестных
где А – матрица коэффициентов перед Элементы матрицы "А" вычисляются по формулам
за исключением коэффициентов главной диагонали матрицы:
Элементы матрицы "В" будут равны:
Система (9.12) может быть решена одним из стандартных методов (метод исключения Гаусса и др.). Однако при многовариантных расчетах в одной и той же геометрической системе наиболее экономичным является метод обращения матрицы, Это связано с тем, что в расчетах изменяемой величиной обычно является температура, а матрица "А" не зависит от температуры. Согласно этому методу вычисляется, так называемая, обратная матрица
элементы которой обозначим через
С учетом (9.16) из выражения (9.12) в явном виде определяется поток эффективного излучения для любой зоны "j".
или
Найденные таким образом Обратная и смешанная задачи излучения решаются почти аналогично прямой задаче, но с небольшими отличиями. Эти задачи предполагают, что известны потоки результирующего излучения
Это выражение можно представить в виде
При решении чисто обратной задачи излучения требуется решать систему из N уравнений, подобных (9.20) с N неизвестными После того, как найдены потоки эффективного излучения
Теперь из (9.1) вычисляется
На этом заканчивается решение обратной и смешанной задач излучения.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 464; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.175.191 (0.01 с.) |


 , (9.1)
, (9.1) – степень черноты i-й зоны;
– степень черноты i-й зоны;  – коэффициент излучения абсолютно черного тела, равный
– коэффициент излучения абсолютно черного тела, равный 
 ;
;  – температура i-й зоны;
– температура i-й зоны;  . – площадь i-й зоны.
. – площадь i-й зоны. , (9.2)
, (9.2) – поток падающего излучения на i-ю зону.
– поток падающего излучения на i-ю зону. . (9.3)
. (9.3) . (9.4)
. (9.4) . (9.5)
. (9.5) . (9.6)
. (9.6) ? Известна связь через геометрический угловой коэффициент (Г.У.К.) –
? Известна связь через геометрический угловой коэффициент (Г.У.К.) –  :
: , (9.7)
, (9.7) поток падающего излучения с j-й зоны на i-ю зону.
поток падающего излучения с j-й зоны на i-ю зону. . (9.8)
. (9.8)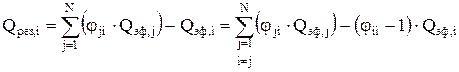 . (9.9)
. (9.9)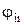 можно отнести к справочным данным. В сложных геометрических системах (плавно изогнутые поверхности, произвольная ориентация поверхностей в пространстве и т.п.) Г.У.К. рассчитывают с использованием вероятностного метода Монте-Карло [12, 13]. К недостаткам метода можно отнести довольно значительную погрешность – 3-5 %, неэкономичность при попытке достичь приемлемой точности. Главное достоинство метода, которое доминирует над всеми недостатками – универсальность. В простых геометрических системах (взаимно параллельные и перпендикулярные плоские поверхности и т.п.), примером которых является рабочее пространство большинства промышленных печей, можно пользоваться стандартными аналитическими формулами [13, 14 и др.] для расчета Г.У.К.
можно отнести к справочным данным. В сложных геометрических системах (плавно изогнутые поверхности, произвольная ориентация поверхностей в пространстве и т.п.) Г.У.К. рассчитывают с использованием вероятностного метода Монте-Карло [12, 13]. К недостаткам метода можно отнести довольно значительную погрешность – 3-5 %, неэкономичность при попытке достичь приемлемой точности. Главное достоинство метода, которое доминирует над всеми недостатками – универсальность. В простых геометрических системах (взаимно параллельные и перпендикулярные плоские поверхности и т.п.), примером которых является рабочее пространство большинства промышленных печей, можно пользоваться стандартными аналитическими формулами [13, 14 и др.] для расчета Г.У.К. необходимо знать
необходимо знать  при j = 1, 2,..., N. Поэтому, предварительно приходится составлять специальную систему уравнений для расчета
при j = 1, 2,..., N. Поэтому, предварительно приходится составлять специальную систему уравнений для расчета  . Это делается следующим образом. Выразим
. Это делается следующим образом. Выразим  (9.10)
(9.10) . (9.11)
. (9.11) также определяются предварительно, т.к. поток собственного излучения не зависит от
также определяются предварительно, т.к. поток собственного излучения не зависит от  , (9.12)
, (9.12) . (9.13)
. (9.13) . (9.14)
. (9.14) , (9.15)
, (9.15) , (9.16)
, (9.16)
 . (9.16)
. (9.16) , (9.17)
, (9.17)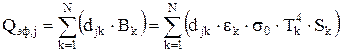 , (9.18)
, (9.18)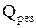 . На этом заканчивается решение прямой задачи излучения зональным методом, т.е. задачи нахождения результирующих тепловых потоков при известных температурах зон.
. На этом заканчивается решение прямой задачи излучения зональным методом, т.е. задачи нахождения результирующих тепловых потоков при известных температурах зон. . (9.19)
. (9.19) . (9.20)
. (9.20) , исходя из (9.5)
, исходя из (9.5) . (9.21)
. (9.21)
 , (9.22)
, (9.22)


