
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неявная конечно-разностная схемаСодержание книги
Поиск на нашем сайте
Неявная схема отличается от явной только тем, что производные по пространственной переменной отнесены к последующему моменту времени – (n+1), а не к текущему
На рис. 5.2 приведены фрагменты разностной сетки, иллюстрирующие с помощью, так называемых, четырехточечных шаблонов (выделены толстыми линиями) определение температуры на последующем шаге по времени.
Рис. 5.2. Шаблоны для определения температуры в (n+1)-й момент времени
Можно заметить, что неявная схема не позволяет в явном виде выразить температуру Довольно сложный алгоритм решения уравнения теплопроводности по неявной схеме в сравнении с явной схемой оправдан, т.к. неявная схема безусловно устойчива и позволяет анализировать поле температур при любом сочетании шагов разностной сетки. Метод прогонки Метод прогонки является самым экономичным методом для решения систем уравнений подобных (5.13). Представим (5.13) в следующем формализованном виде:
где Здесь индексы (n+1) опущены для простоты записи. В уравнении (5.14) только три неизвестные:
где для N равного, например, 5
Матрица коэффициентов Теперь предположим, что между температурами в соседних узлах существует линейная зависимость
где Подставив (5.15) в (5.14), получим уравнение с двумя неизвестными
Отсюда в виде линейной зависимости легко выражается
т.е. предположение (5.15) подтвердилось. Из аналогии (5.17) и (5.15) можно найти коэффициенты
Коэффициенты ai и bi называются прогоночными коэффициентами и они находятся во всех узлах разностной сетки по рекуррентным формулам (5.18) и (5.19). Порядок решения систем уравнений, подобных (5.14), следующий: сначала определяются из граничных условий коэффициенты a1 и b1. Затем по выражениям (5.18) и (5.19) коэффициенты a2, b2; a3, b3 и т.д. до aN-1, bN-1. Эта часть алгоритма называется прямой прогонкой. Далее из граничных условий на противоположной границе находится температура tN и по формуле (5.15) обратной прогонкой последовательно определяются температуры в узлах сетки от (N-1) до 1:
Преимущества метода прогонки перед другими методами – экономичность. Это означает, что при расчетах по этому методу требуется выполнить минимальное число арифметических операций. Например, по методу Гаусса число операций
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 1199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.147.193 (0.005 с.) |

 при
при 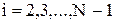 . (5.13)
. (5.13)
 через известные температуры в соседних узлах. Поэтому уравнение (5.13) записывают для всех узлов сетки по сечению тела, за исключением граничных: первого и N-го. Уравнения для граничных узлов берутся из граничных условий, которые мы будем рассматривать позже. В общей сложности образуется система из N уравнений с N неизвестными температурами на (n+1) шаге по времени. Эту систему можно решить любым стандартным методом. Но дело в том, что любой метод здесь меньше всего подходит. Для решения данной системы уравнений разработан специальный метод, который назвали "метод прогонки". В иностранной литературе этот метод называется "алгоритм Томаса"[9].
через известные температуры в соседних узлах. Поэтому уравнение (5.13) записывают для всех узлов сетки по сечению тела, за исключением граничных: первого и N-го. Уравнения для граничных узлов берутся из граничных условий, которые мы будем рассматривать позже. В общей сложности образуется система из N уравнений с N неизвестными температурами на (n+1) шаге по времени. Эту систему можно решить любым стандартным методом. Но дело в том, что любой метод здесь меньше всего подходит. Для решения данной системы уравнений разработан специальный метод, который назвали "метод прогонки". В иностранной литературе этот метод называется "алгоритм Томаса"[9]. при
при  (5.14)
(5.14)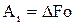 ;
; 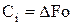 ;
;  ;
;  ;
;  .
.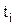 ,
,  ,
,  . Это определяет специфический вид матрицы связанных коэффициентов в системе уравнений (5.14). В матричной форме система уравнений имеет вид
. Это определяет специфический вид матрицы связанных коэффициентов в системе уравнений (5.14). В матричной форме система уравнений имеет вид ,
, ;
;  ;
; 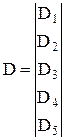 .
. , (-Bi) и Ci носит название разреженной 3-х диагональной, поскольку она заполнена нулями кроме 3-х главных диагоналей. В этом, кстати, ограниченность метода прогонки: он может применяться при решении систем уравнений только с 3-х диагональной матрицей связанных коэффициентов.
, (-Bi) и Ci носит название разреженной 3-х диагональной, поскольку она заполнена нулями кроме 3-х главных диагоналей. В этом, кстати, ограниченность метода прогонки: он может применяться при решении систем уравнений только с 3-х диагональной матрицей связанных коэффициентов.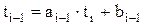 , (5.15)
, (5.15) и
и 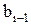 – некоторые коэффициенты.
– некоторые коэффициенты. . (5.16)
. (5.16) , (5.17)
, (5.17) и
и 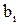 :
: ; (5.18)
; (5.18) (5.19)
(5.19) ;
;  ; …;
; …;  ; …
; …  .
. , а по методу прогонки
, а по методу прогонки 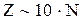 . Так, если число узлов по сечению тела N = 100, то по методу Гаусса получим порядка 1 000 000 арифметических действий, а по методу прогонки – всего 1 000.
. Так, если число узлов по сечению тела N = 100, то по методу Гаусса получим порядка 1 000 000 арифметических действий, а по методу прогонки – всего 1 000.


