
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные численные соотношенияСодержание книги
Поиск на нашем сайте
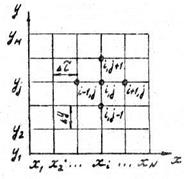
Для определенности рассмотрим двумерную задачу в координатах "х-у". как показано на рис.6.1а. Также, как и для нестационарных задач, метод конечных разностей предполагает замену непрерывной области изменения пространственных переменных х и у рядом дискретных узлов: х: х1, х2, х3,..., xi,..., xN и у: у1, у2, у3,...,уj,...,yМ, где N и M – число узлов по координатам х и у. Расстояние между узлами называется шагом:
В соответствии с принятыми обозначениями, нанесем на расчетную область ряд узлов (рис.6.1б). Полученное построение называется разностной сеткой. Значения температуры определяются в узлах этой сетки. Математически метод конечных разностей заключается в замене интегрирования уравнения Лапласа системой алгебраических уравнений, записанных для каждого узла разностной сетки. Для перевода дифференциального уравнения в алгебраический вид в окрестностях узлов с номерами i и j удобно пользоваться разностями "вперед" и "назад". Разности "вперед":
Разности "назад":
Рис.6.1. Формирование разностной сетки для двумерной задачи стационарной теплопроводности
С использованием этих разностей двумерное уравнение Лапласа в окрестности внутреннего узла с координатами i j будет иметь вид
при i = (2, 3, …,N-1); j = (2, 3, …, M-1) или Умножим все члены уравнения на
Отсюда легко выражается
Уравнение (6.5) является основным уравнением для расчета стационарного температурного поля. Анализ уравнения показывает, что для расчета температуры в узле ij надо знать температуру во всех соседних узлах ("i+1, j", "i-1, j", "i, j+1", "i, j-1"). При непосредственных вычислениях задача заключается в определении температур во всех узлах разностной сетки, подчиняющихся соотношению (6.5). Для определения этих температур существуют явная и неявная схемы расчета. При изложении этих схем примем для упрощения записи, что
Тогда Явная разностная схема Явная схема обычно представляется в виде
где n= 0, 1,... – номер итерационного шага; w – итерационный параметр. Особенность явной схемы в том, что температура в процессе итерационного счета выражается в явном, достаточно простом виде без решения систем уравнений.
Явная схема устойчива при w £ 1. Последовательность расчета температурного поля приведена на блок-схеме рис.6.2. В блоке 4 формула (6.7) приведена условно, поскольку она справедлива только для внутренних узлов сетки. Естественно, что для граничных узлов должны быть использованы другие формулы (см. разд.6.4).' Основная сложность расчета заключается в выборе итерационного параметра "w". От него зависит сходимость решения. Самая низкая скорость при w = 1. Этот случай известен под названием метод Якоби. Однако на практике схема (6.7) используется редко из-за своих недостатков: – низкая скорость сходимости; – узкие пределы варьирования итерационного параметра; – необходимость при расчетах на ЭВМ пользоваться двумя массивами температур
Рис. 6.2. Логическая блок-схема для расчета стационарного температурного поля по явной схеме
Этих недостатков лишена явная схема Зейделя, в соответствии с которой имеем
Здесь предполагается, что Неявная разностная схема Неявная разностная схема выводится из того положения, что стационарное температурное поле является установившимся случаем нестационарного поля при бесконечно большом времени протекания процесса нагрева. При. этом итерационный параметр "w" играет роль шага по времени в эквивалентном уравнении теплопроводности:
при i = (2, 3,..., N-1) и j = (2, 3,..., M-1) (рис.6.1б). Для того, чтобы определить температуру на (n+1)-й итерации, надо решить систему уравнений типа (6.9), записанных для каждого внутреннего узла разностной сетки, плюс набор уравнений для граничных узлов. В целом получается система (N M)- уравнений с (N M)- неизвестными температурами. Причем, матрица связанных коэффициентов перед температурами – пятидиагональная. Такую систему линейных алгебраических уравнений надо решать или методом исключения Гаусса или методом обращения матриц или итерационным методом, т.е. методами, которые требуют значительного количества арифметических операций при реализации на ЭВМ. В попытке отойти от этих неэкономичных методов возникли модификации неявной схемы, которые по аналогии с решением многомерных нестационарных задач теплопроводности разделили на локально-одномерную и продольно-поперечную схемы. Эти схемы позволяют свести указанные системы уравнений к системам с трехдиагональными матрицами связанных коэффициентов и, в конечном счете, позволяют применить метод прогонки решения системы уравнений. На практике целесообразно применять продольно-поперечную схему, обладающую наиболее высокой скоростью сходимости. Эта схема записывается в виде 2-х уравнений:
по направлению х:
при i = (2, 3, …, N-1) и по направлению у:
при j = (2, 3,..., M-1). Алгоритм решения задачи по этой схеме приведен на рис.6.3.
Рис. 6.3. Логическая блок-схема расчета стационарного температурного поля по неявной схеме
Особенность алгоритма состоит в расчете промежуточного значения температуры на (n+1/2) итерационном шаге, которая является исходной для окончательного расчета на (п+1)-м шаге. Для указанной выше неявной схемы итерационный параметр "w" может принимать произвольное значение. Его можно подобрать таким, что резко будет увеличена скорость сходимости, т.е. решение будет получено за минимальное число итераций.
|
||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.165.134 (0.011 с.) |

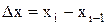 – шаг по координате х;
– шаг по координате х; – шаг по координате у.
– шаг по координате у. и
и  . (6.2)
. (6.2)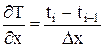 и
и  . (6.3)
. (6.3)
 (6.4)
(6.4) .
. и введем обозначение
и введем обозначение  . Тогда
. Тогда .
. :
: . (6.5)
. (6.5)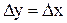 и К = 1.
и К = 1. . (6.6)
. (6.6) , (6.7)
, (6.7)
 . (6.8)
. (6.8) , и
, и 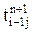 уже известны. Схема Зейделя гораздо эффективнее обычной явной схемы. Она устойчива при 0 £ w £ 2. Когда w<1, то расчет осуществляется методом последовательной нижней релаксации (ПНР), а когда 1 < w £ 2, то расчет носит название метод последовательной верхней релаксации (ПВР). Метод ПВР обычно позволяет достичь более высокой скорости сходимости. Рекомендуется принимать w=1,6¸1,8 для минимизации числа итерационных шагов.
уже известны. Схема Зейделя гораздо эффективнее обычной явной схемы. Она устойчива при 0 £ w £ 2. Когда w<1, то расчет осуществляется методом последовательной нижней релаксации (ПНР), а когда 1 < w £ 2, то расчет носит название метод последовательной верхней релаксации (ПВР). Метод ПВР обычно позволяет достичь более высокой скорости сходимости. Рекомендуется принимать w=1,6¸1,8 для минимизации числа итерационных шагов.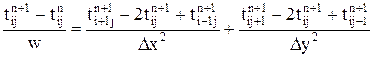 (6.9)
(6.9) (6.10)
(6.10) (6.11)
(6.11)



