
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные численные методы расчета нагрева в печи термически тонких телСодержание книги
Поиск на нашем сайте
Изучение методов численного моделирования теплообмена лучше начинать с разбора методов расчета нагрева твердых термически тонких тел (ТТТ), поскольку это наиболее простые методы, лежащие и основе более сложных методов, описанных в последующих разделах, касающихся теплопроводности и конвекции. Представим себе абстрактную печь, в которой на поду лежит заготовка, обладающая свойством термически тонкого тела и нагреваемая конвекцией и излучением. Такая заготовка может представлять из себя, например, медный пруток. Напомним, что термически тонким телом называют тело, при нагреве которого можно пренебречь перепадом температур в объеме этого тела. Важнейшим выводом этого определения будет равенство среднемассовой температуры и температуры поверхности тела. Последнее замечание позволяет рассматривать процесс нагрева только во времени, исключая из анализа процесс теплопроводности. Пусть температуры кладки и газа рассматриваемой печи постоянны в процессе нагрева и равны Ткл и Тг соответственно. Причем газ возьмем лучепрозрачным. Тогда процесс нагрева можно описать в виде дифференциального уравнения
где Левая часть уравнения представляет собой приращение энтальпии тела, а правая часть – результирующий тепловой поток на заготовку. Т.е по своей сути уравнение является обычным балансовым соотношением. В математике уравнение (4.1) называют обыкновенным дифференциальным уравнением (О.Д.У.). Для того, чтобы задача нагрева была определена во времени, нужно задаться начальным условием
Из системы уравнений (4.1-4.2) требуется определить температуру металла в любой момент времени. Несмотря на свою внешнюю простоту, задача в общем виде не может быть решена аналитически и поэтому для ее решения используют численные методы. В частном случае, когда температуры тел, участвующих в теплообмене, не изменяются во времени и производная в левой части (4.1) равна нулю, система дифференциальных уравнений (4.1-4.2) превращается в алгебраическое уравнение
Поскольку в уравнении (4.3) неизвестная температура металла присутствует в 1-й и одновременно в 4-я степени, то это уравнение является нелинейным и поэтому решается одним из итерационных методов (метод половинного деления, метод Ньютона и др.), изложенных в справочной литературе по математике.
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.77.40 (0.009 с.) |

 , (4.1)
, (4.1) – удельная теплоемкость заготовки, зависящая от температуры, Дж/(кг К);
– удельная теплоемкость заготовки, зависящая от температуры, Дж/(кг К);  – масса заготовки, кг;
– масса заготовки, кг; 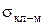 – приведенный коэффициент излучения в системе тел "кладка-металл", Вт/(м2×К4);
– приведенный коэффициент излучения в системе тел "кладка-металл", Вт/(м2×К4);  – площадь теплообменной поверхности металла, м2;
– площадь теплообменной поверхности металла, м2;  – тепловой поток потерь в окружающую среду, Вт.
– тепловой поток потерь в окружающую среду, Вт. . (4.2)
. (4.2) . (4.3)
. (4.3)


