
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рабочие характеристики математических моделейСодержание книги
Поиск на нашем сайте Хорошая математическая модель теплообмена должна соответствовать следующим требованиям: · точность расчетов; · адаптированность результатов; · универсальность структуры; · экономичность реализации. Разберем характеристики моделей, отражающие эти требования. 1. Точность расчета чаще всего оценивают через погрешность в абсолютных величинах
или в относительных единицах
где Yрасч..и Yист. – приближенное (расчетное) и истинное значение исследуемого параметра. Эта погрешность может быть вызвана следующими причинами: а) с неучетом в модели отдельных связей и параметров реальной печи; б) с недостатками метода численной реализации модели; в) с ошибками округления при большом числе вычислительных операций; г) с невнимательностью расчетчика. Последняя причина (г) определяет возникновение случайной погрешности. Остальные причины (а-в) могут дать, так называемую, систематическую погрешность. Из систематической погрешности, погрешность, связанная с (а), является модельной, а связанная с (б) и (в) – вычислительной. Случайная и вычислительная погрешности, которые присутствуют в результатах расчета по модели, поддаются выявлению и оценке с помощью тестовых примеров, составленных для идеализированных случаев. При этом случайная погрешность должна быть исключена, а вычислительная – уменьшена до минимума. Что касается модельной погрешности, то она косвенно учитывается и нейтрализуется при проведении процедуры адаптации (см. ниже) путем введения в модель настроечных коэффициентов. Если после проведения процедуры адаптации модельная погрешность недопустимо высока, то можно сделать вывод о том, что модель не отражает реальную природу процесса и что погрешность в какой-то степени носит случайный характер. 2. Адаптированность результатов При согласовании результатов расчета с экспериментальными (реальными) данными исходят из того, что и те и другие содержат некоторую погрешность. Так, результаты расчета содержат погрешность из-за несовершенства и ограниченности математической модели, что является недостатком любой сложной модели. Экспериментальные данные имеют погрешность из-за недостаточной точности приборов, ошибок измерения и наличия неконтролируемых факторов, мешавших проведению замеров. По этим причинам, прежде чем сопоставлять расчет с экспериментом, надо оценить погрешность экспериментальных замеров, например, через дисперсию эксперимента – Дэ. Когда сравнивают расчет с экспериментом, то вводят понятие адекватности (соответствия). При хорошем согласовании расчета и эксперимента говорят: "модель адекватно описывает процессы в реальной печи (или другом объекте)". Численным показателем соответствия расчетных и экспериментальных данных может служить дисперсия адекватности – Да или другие оценочные величины (подробнее в разд. 11). Дисперсия адекватности должна примерно соответствовать дисперсии эксперимента Да» Дэ. Если в результате проверки на адекватность получилось, что модель не адекватна экспериментальным данным, то надо пересмотреть и уточнить подход к составлению модели. Если же Да << Дэ, то надо или заменить модель на более грубую, или увеличить точность экспериментальных замеров. 3. Универсальность структуры Простота внесения изменений и дополнений в модель определяется уровнем универсальности модели. Достаточно универсальная модель строится на модульном подходе. Она состоит из набора небольших самостоятельных моделей, называемых модулями (подробнее в разд. 3). 4. Экономичность реализации Последняя важная характеристика математических моделей это экономичность, т.е. малый объем математических операций при расчете по этой модели. Экономичность моделей способствует не только экономии машинного времени, но и повышает точность расчета за счет уменьшения ошибок округления. Лучше всего, если математическая модель может быть реализована в процессе ручных вычислений. Но таких моделей сейчас практически не осталось, т.к. обычно простота моделей соответствует низкой точности результатов расчета. Одновременно с усложнением моделей разрабатываются новые схемы вычислений, называемые экономичными, и новые методы расчета по этим экономичным схемам. Например, при моделировании задач теплопроводности методом конечных разностей приходится решать систему алгебраических уравнений специального вида, для которых разработан экономичный метод прогонки (разд. 6).
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

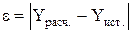 (2.1)
(2.1)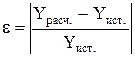 (2.2)
(2.2)


