
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многомерные задачи теплопроводностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для простоты разберем двумерную задачу теплопроводности. В этом случае температурное поле внутри тела описывается уравнением теплопроводности вида
где при соответствующих граничных условиях, например, типа
и при начальных условиях, типа
Точно также, как и при рассмотрении одномерных задач, будем искать численные соотношения только для уравнения теплопроводности (5.27). В соответствии с основной идеей метода конечных разностей непрерывная область изменения пространственных переменных "
по по и по
Расстояние между узлами называется шагом и обозначается
Разностную сетку, т.е. графическое изображение совокупности узлов, для многомерных задач представить довольно тяжело. Обычно для двумерной задачи на разностной сетке отсутствует координата по времени, но она подразумевается (рис. 5.3).
Рис. 5.3. Разностная схема для двумерной задачи теплопроводности
Проведем разностную аппроксимацию уравнения (5.27) в окрестности узла с координатами (i, j, n). Тогда при замене сеточных функция точного решения
Это явная разностная схема. Название схемы связано с тем. что из (5.30) в явном виде выражается неизвестное значение температуры
В частном случае, когда
Таким образом, условие устойчивости для многомерных задач по сравнению с одномерными (5.12) более жесткое. Представим теперь уравнение теплопроводности (5.27) в неявном конечно-разностном виде. Для этого вторую производную по пространству отнесем к последующему (n+1)-му моменту времени. Получим
Очевидно, что неизвестными в (5.33) являются пять величин: Для того, чтобы уменьшить объем вычислительных операций, разработаны схемы и методы, при реализации которых на ЭВМ объем арифметических операций пропорционален числу уравнений – Локально-одномерная схема Локально-одномерная схема позволяет свести уравнение (5.33) к двум одномерным уравнениям: а) по направлению х:
б) по направлению у:
Порядок расчета по этой схеме следующий: 1. Сначала находится значение фиктивной температуры 2. Далее, исходя из известного поля фиктивных температур Несколько коротких характеристик схемы: а) она самая экономичная из известных на сегодняшний день схем, имеющих погрешность б) схема является сходящейся и безусловно устойчивой. Продольно-поперечная схема Данная схема родилась из локально-одномерной с целью увеличения скорости сходимости последней. Подход к ее формированию напоминает подход, изложенный в схеме Кранка-Николсона для одномерных задач. Продольно-поперечная схема представляет из себя аппроксимацию уравнения теплопроводности в следующем виде: а) по направлению "х":
при i = 2,3,...,N-1; j = 1,2,...,M.
б) по направлению "у":
при j = 2,3,...,M-1; i = 1,2,...,N.
Последовательность расчета та же, что и для реализации локально-одномерной схемы. Схема является безусловно устойчивой.
Погрешность схемы ~
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 734; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

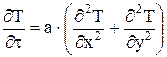 . (5.27)
. (5.27) ;
; 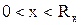 ;
; 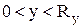
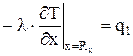 ;
;  (5.28)
(5.28) . (5.29)
. (5.29)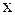 " и "
" и " 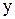 " и временной переменной "
" и временной переменной " 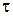 " заменяется на ряд дискретных узлов с координатами:
" заменяется на ряд дискретных узлов с координатами: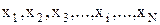 ;
;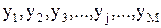 ;
;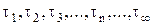 .
.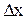 и
и  и временной переменной
и временной переменной  . Таким образом, шаги можно определить так:
. Таким образом, шаги можно определить так: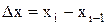 ;
;  ;
; 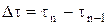 .
.
 на сеточную функцию приближенного решения
на сеточную функцию приближенного решения  получим
получим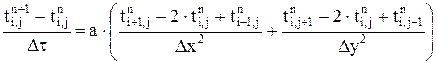 , (5.30)
, (5.30)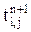 через известные значения
через известные значения  ,
,  ,
, 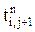 ,
, 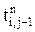 – определенные на текущем шаге по времени. Схема является условно устойчивой. Условие устойчивости для двумерной задачи имеет вид:
– определенные на текущем шаге по времени. Схема является условно устойчивой. Условие устойчивости для двумерной задачи имеет вид: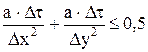 или
или 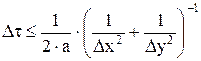 . (5.31)
. (5.31)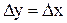 , получим
, получим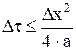 . (5.32)
. (5.32)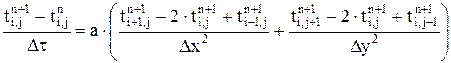 . (5.33)
. (5.33) ,
, 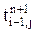 ,
,  ,
, 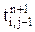 . В этом случае, чтобы определить температуру во всех узлах разностной сетки на (n+1)-м шаге по времени надо решать систему уравнений подобных (5.33), записанных для каждого узла. Вид системы уравнений специфический. Матрица коэффициентов перед неизвестными температурами носит название пятидиагональной. Следовательно, для решения системы уравнений не может быть применен метод прогонки и приходится пользоваться иными методами (метод исключения Гаусса, метод определителей и др.), что нежелательно в силу их неэкономичности. Напомним, что неэкономичность может привести к значительной вычислительной погрешности в результате округлений чисел, а также к увеличению времени расчета на ЭВМ.
. В этом случае, чтобы определить температуру во всех узлах разностной сетки на (n+1)-м шаге по времени надо решать систему уравнений подобных (5.33), записанных для каждого узла. Вид системы уравнений специфический. Матрица коэффициентов перед неизвестными температурами носит название пятидиагональной. Следовательно, для решения системы уравнений не может быть применен метод прогонки и приходится пользоваться иными методами (метод исключения Гаусса, метод определителей и др.), что нежелательно в силу их неэкономичности. Напомним, что неэкономичность может привести к значительной вычислительной погрешности в результате округлений чисел, а также к увеличению времени расчета на ЭВМ. , а не
, а не  как у обычных методов. Такие схемы называются экономичными. Из них наиболее распространены локально-одномерная схема и продольно-поперечная схема. Они основаны на замене многомерной разностной схемы системой одномерных разностных схем.
как у обычных методов. Такие схемы называются экономичными. Из них наиболее распространены локально-одномерная схема и продольно-поперечная схема. Они основаны на замене многомерной разностной схемы системой одномерных разностных схем.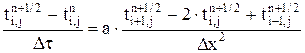 (
(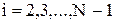 ;
; 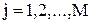 ). (5.34)
). (5.34) (
(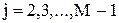 ;
; 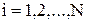 ). (5.35)
). (5.35)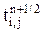 на промежуточном (n+1/2) шаге по времени. Для этого методом прогонки решается система уравнений подобных (5.34) совместно с граничными условиями по направлению "х".
на промежуточном (n+1/2) шаге по времени. Для этого методом прогонки решается система уравнений подобных (5.34) совместно с граничными условиями по направлению "х".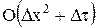 ;
;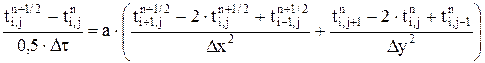 (5.36)
(5.36)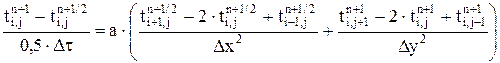 (5.37)
(5.37) . Если сравнивать локально-одномерную и продольно-поперечную схемы по экономичности расчета на одном шаге по времени, то локально-одномерная более эффективна. Но если принимать во внимание требуемое число шагов по времени и соответствующее числу шагов число арифметических операций для достижения одинаковой точности результатов, то продольно-поперечная схема имеет несомненные преимущества.
. Если сравнивать локально-одномерную и продольно-поперечную схемы по экономичности расчета на одном шаге по времени, то локально-одномерная более эффективна. Но если принимать во внимание требуемое число шагов по времени и соответствующее числу шагов число арифметических операций для достижения одинаковой точности результатов, то продольно-поперечная схема имеет несомненные преимущества.


