
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие понятия численных методов при моделировании нагрева ТТТСодержание книги
Поиск на нашем сайте
Для придания общности последующим рассуждениям приведем уравнение (4.1) к следующему формализованному виду [15]
где Начальное условие остается прежним (4.2). Понятно, что, если изменится вид результирующих тепловых потоков на металл или будут другие изменения в записи баланса (4.1), то они будут отражены только в функции (4.5). Вид записи (4.4) останется неизменным. Будем называть уравнение (4.4) общей формой обыкновенного дифференциального уравнения (О.Д.У.). Несколько забегая вперед, отметим, что численное решение ОДУ заключается в замене производной ее дискретным аналогом. При этом непрерывная область изменения независимой переменной
Рис. 4.1. Температурная диаграмма нагрева с сеточной дискретизацией по времени
Для равномерной сетки
где N – число узлов сетки не включая начальный. Кроме равномерных сеток существуют неравномерные сетки, т.е. сетки, в которых шаг зависит от номера узла. В этом случае время нагрева определяется следующим образом
Для простоты изложения материала будем рассматривать только равномерные сетки. Таким образом, после формирования сетки вместо задачи отыскания непрерывной функции Т(t) получаем задачу нахождения функции Tj, определенной только в узлах сетки – j. Величина Тj называется сеточной функцией точного решения. При численном решении дифференциальное уравнение заменяется алгебраическим по соотношениям
где символ О(Dt) используется для обозначения порядка малой величины. Этот символ является первой буквой слова Ordo (порядок – лат.) Если пренебречь малой величиной О(Dt), то этим вносится погрешность и точного решения в узлах получить практически невозможно. Любое решение будет приближенным. Поэтому, вводится понятие: сеточная функция разностного решения, которую обозначим tj. Таким образом, если мы хотим найти решение дифференциального уравнения численным методом, то точного решения (Tj) не получим, а получим приближенное решение (tj) в узлах разностной сетки. Естественно, что погрешность численного решения равна разности между точным и приближенным значением функции
Погрешность численного решения (ej) зависит от того, каким способом (методом) перешли от дифференциального уравнения к алгебраическому. Разные методы определяют и разный вид алгебраических уравнений. Систему алгебраических уравнений, решаемую относительно tj (j = 1,2,...,N), называют разностной схемой. Разностные схемы бывают сходящиеся и расходящиеся. Расходящиеся схемы являются недопустимыми для расчетов, т.к. погрешность расчетов по этим схемам при уменьшении шага по времени возрастает или, по крайней мере, не уменьшается. Если при
то схема является расходящейся. Решение можно получить только на сходящейся схеме, т.е. когда при
Понятно, что мы должны стремиться к созданию и использованию сходящихся разностных схем. Т.о. погрешность численного решения (
где А – коэффициент пропорциональности (А = const); p – параметр, имеющий свое особое название – порядок точности. Порядок точности характеризует скорость убывания погрешности или скорость сходимости решения при измельчении разностной сетки. Так. если
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.28.111 (0.006 с.) |

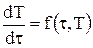 при
при  , (4.4)
, (4.4)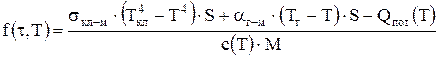 . (4.5)
. (4.5) заменяется множеством дискретных (фиксированных) значений, которые называются узлами сетки, наносимой на температурную диаграмму нагрева (рис. 4.1).
заменяется множеством дискретных (фиксированных) значений, которые называются узлами сетки, наносимой на температурную диаграмму нагрева (рис. 4.1).
 . Здесь
. Здесь  – шаг сетки
– шаг сетки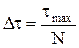 , (4.6)
, (4.6) .
.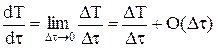 , (4.7)
, (4.7) . (4.8)
. (4.8) и
и 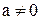
 , (4.9)
, (4.9) . (4.10)
. (4.10) ) зависит от шага изменения независимой переменной времени –
) зависит от шага изменения независимой переменной времени –  , (4.11)
, (4.11)


