
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость разностной схемы ЭйлераСодержание книги
Поиск на нашем сайте
Как отмечалось в разделе 4.1, разностные схемы бывают сходящимися и расходящимися. Сходимость схемы связана с погрешностью аппроксимации схемы и зависит от вида разностной схемы. Однако малая погрешность аппроксимации еще не гарантирует получения решения. При определенных условиях в процессе вычислений может возникнуть неустойчивость решений. Пример неустойчивого решения показан на рис. 4.2. Разностные схемы называются устойчивыми, если малые погрешности, допущенные в процессе расчетов (округление и т.п.), затухают или остаются малыми при неограниченном увеличении числа шагов по времени [10]. В данном случае на рис. 4.2 численное решение представляет из себя функцию во времени с быстро нарастающей амплитудой колебаний. С уменьшением шага
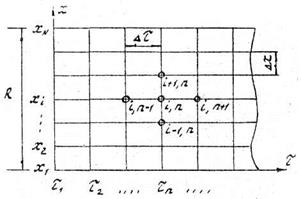
Рис. 4.2. Изменение температуры материала во времени при использовании неустойчивой разностной схемы: 1 – точное решение; 2 – численное решение по неустойчивой схеме Эйлера КОНЕЧНО-РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ТЕПЛОПРОВОДНОСТИ (НАГРЕВ ТЕРМИЧЕСКИ МАССИВНЫХ ТЕЛ) При решении задач нагрева термически массивных тел рассматривают системы с пространственно-временными полями температур, т.е. когда температуры изменяются не только во времени, но и в объеме тел. В этом отличие процесса нагрева термически массивных тел от процесса нагрева термически тонких тел. Задачи теплопроводности описываются дифференциальными уравнениями в частных производных по пространству и времени с соответствующими начальными и граничными условиями. Особенность решения этих задач методом конечных разностей по сравнению с другими численными методами в том, что дискретизация дифференциальных уравнений, т.е. перевод уравнений в алгебраический вид, производится на исходных уравнениях без какой-либо промежуточной обработки. Таким образом, составляется система алгебраических уравнений, решаемая относительно искомых температур в дискретных узлах во времени и пространстве. При этом результат решения является приближенным с заданной степенью точности. Основные понятия теории разностных схем Основная идея метода конечных разностей заключается в том, что непрерывная область изменения пространственной и временной переменных заменяется конечным числом дискретно расположенных узловых точек: по пространству: и по времени: Расстояние между узлами называется шагом. Например, Для случая одномерной задачи набор узловых точек представлен на рис. 5.1. Такая система узловых точек, соединенных между собой, называется разностной сеткой. Каждый узел сетки имеет свои координаты (i, n) или ( Если шаг сетки по пространству и по времени равномерный, то текущие значения координат определяются из соотношений
Рис. 5.1. Разностная сетка для одномерной задачи теплопроводности
Для неравномерной сетки шаг по времени и пространству может изменяться произвольным образом. Этот случай мы не рассматриваем. Покажем как перейти от производной к ее алгебраическому аналогу, используя разностную сетку. По определению производной, если есть непрерывная и дифференцируемая функция, то ее производная будет равна
где Таким образом, производная определяется параметрами в соседних, достаточно близких, точках (узлах) пространства. Если принять, что
При аппроксимации производной величиной Существуют 3-и основных способа представления производных по пространству в точке i: разность "назад" (левая разность)
разность "вперед" (правая разность)
и центральная разность
Аппроксимируя производную по времени в точке "n", всегда берут разность "вперед" или разность "назад"
т.к. при использовании центральной разности расчет неустойчив. Вторую производную чаше всего представляют в виде:
Такие понятия, как погрешность численного решения ( Так, разности "вперед" и "назад" (5.4, 5.5, 5.7) имеют погрешность, пропорциональную соответствующему шагу в 1-я степени (1-й порядок точности), а центральная разность (5.6) – шагу во 2-й степени (2-й порядок точности). Аппроксимация второй производной в виде (5.8) также имеет 2-й порядок точности.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 568; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.146.108 (0.007 с.) |

 можно убрать колебательный характер решения. Важно также помнить, что неустойчивость может возникнуть только при использовании явной схемы и определенных шагах
можно убрать колебательный характер решения. Важно также помнить, что неустойчивость может возникнуть только при использовании явной схемы и определенных шагах  , где
, где  – порог устойчивости. Поэтому явные схемы получили название условно устойчивых. Неявные схемы Эйлера безусловно устойчивы.
– порог устойчивости. Поэтому явные схемы получили название условно устойчивых. Неявные схемы Эйлера безусловно устойчивы.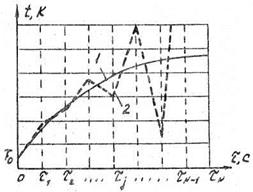


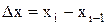 – шаг по координате,
– шаг по координате, 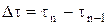 – шаг по времени.
– шаг по времени. ), при которых определяется температура.
), при которых определяется температура. ; (5.1)
; (5.1) .
.
 , (5.2)
, (5.2) – изменение функции, соответствующее малому приращению координаты –
– изменение функции, соответствующее малому приращению координаты – 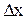 ;
; 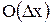 – малая величина, имеющая порядок
– малая величина, имеющая порядок  ..(5.3)
..(5.3)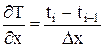 (5.4)
(5.4) (5.5)
(5.5) (5.6)
(5.6) или
или  , (5.7)
, (5.7)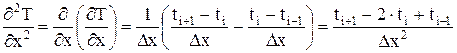 . (5.8)
. (5.8) ), разностная схема, сходимость, устойчивость схем, порядок точности и другие, описанные в разделе 4, сохраняются и при использовании метода конечных разностей для аппроксимации дифференциальных уравнении в частных производных.
), разностная схема, сходимость, устойчивость схем, порядок точности и другие, описанные в разделе 4, сохраняются и при использовании метода конечных разностей для аппроксимации дифференциальных уравнении в частных производных.


