
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы исследования работы печейСодержание книги
Поиск на нашем сайте ВВЕДЕНИЕ Данное учебное пособие составлено на основе опыта преподавания автором таких дисциплин, как "Моделирование печей и их элементов", "Элементы теории систем и численные методы моделирования тепломассопереноса" и "Применение ЭВМ для моделирования и оптимизации промышленных печей". Объем учебного пособия рассчитан на 28-36 часов лекции и предназначен для студентов 3-4 курсов. Считается, что читатель знаком с общими закономерностями теплообменных процессов, происходящих в печи. Теперь же надо научиться использовать эти закономерности для получения конкретных численных (числовых) значения показателей работы печей. Одна из целей представленных ниже материалов: научиться прогнозировать температуры, тепловые потоки, скорости и расходы теплоносителей в любом тепловом агрегате и, тем более, в печи. Такой прогноз мы будем давать путем моделирования, причем, моделирования на основе ЭВМ. Моделирование – это процесс создания и использования моделей, имитирующих работу какого-либо объекта. В свою очередь, модель можно определить так: "модель – это объект, созданный для воспроизведения некоторого другого объекта, называемого натурой" [1]. Основные затруднения, связанные с моделированием работы печей возникают при учете множества взаимосвязанных сложных печных процессов. В таких сложных объектах, как печи, всегда присутствуют вероятностные и детерминированные процессы. Вероятностные процессы обычно вызваны постепенным износом агрегата в процессе эксплуатации и соответственным изменением его характеристик, а также квалификацией обслуживающего персонала. Наличие вероятностных процессов затрудняет сравнение результатов моделирования с реально существующими показателями печей. Детерминированные процессы – это процессы и связи, действующие в любой ситуации четко определенным образом. Моделирование работы печей на ЭВМ направлено, главным образом, для исследования детерминированных процессов, но существуют отдельные виды моделирования или методы исследования, позволяющие учитывать и вероятностный характер работы печей. Настоящая работа состоит из 11 больших разделов, расположенных в логической последовательности: сначала даются общие положения (разд. 1 и 2), затем разбирается структурный подход к разработке моделей печей (разд. 3), описываются методы расчета теплообмена в рамках отдельных суперблоков общей структуры (разд. 4-9) и приводится пример построения математической модели (разд. 10). При моделировании теплообмена мы исходим из того, что разработка модели не является самоцелью. Модель должна быть приспособлена для практических расчетов и поэтому в работе отдельно выделены вопросы проведения процедуры адаптации модели по экспериментальным данным (разд. 11). Необходимо кратко пояснить структуру материалов, представленных в разделах 4-9. Во-первых, мы ограничились задачами, позволяющими в полной мере рассчитать теплообмен и оценить тепловую работу только пламенных нагревательных и термических печей. Опущены такие большие разделы, как плавление материалов, теплообмен в слое материалов, нагрев металла в индукционных печах. Во-вторых, из-за ограниченности объема курса остались не рассмотренными вопросы моделирования теплообмена в печах на основе инженерных методик. Упор сделан на численные методы расчета, которые обычно остаются в "тени" при чтении таких дисциплин, как "Тепломассоперенос" и "Механика жидкостей и газов". Работа во многом состоялась благодаря атмосфере творчества и доброжелательности, присущей кафедре теплотехники и экологии металлургических печей Национальной металлургической академии Украины. Автор считает своим долгом выразить глубокую благодарность своему учителю проф. Губинскому В.И., а также своим коллегам проф. Свинолобову Н.П., проф. Аверину С.И., доц. Литовченко Ю.К. и доц. Решетняку С.И. за полезные замечания и советы при подготовке учебного пособия. Особую признательность автор выражает Бровкиной С.В. за большой труд по набору рукописи на ПЭВМ и всестороннюю помощь. Все пожелания, по улучшению содержания учебного пособия будут приняты автором с благодарностью. Физическое моделирование В процессе физического моделирования строится геометрический (натурный) аналог исследуемой печи в пропорциональных размерах. При этом характеристики печи-оригинала и печи-аналога имеют одинаковую физическую природу. Необходимым условием является равенство определяющих критериев (чисел) подобия оригинала и аналога. Физические модели разделяют на изотермические (холодные) и теплые. На холодных моделях можно исследовать, главным образом, качественную картину движения газов и материалов в печи. Теплые модели применяются для исследования не только процессов движения, но и для изучения закономерностей теплообмена. Физические модели относительно дешевы, но их недостаток в том, что достаточно надежные и точные результаты получаются на моделях максимально приближенных к реальным, а увеличение размеров, что совершенно логично, приводит к удорожанию моделей. Главный же недостаток физического моделирования, как метода, в практической невозможности определения наилучших конструктивных параметров печи, поскольку каждый вариант конструкции печи практически надо создавать заново. Этих недостатков лишено математическое моделирование. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТЕПЛООБМЕНА В ПЕЧИ. ОСНОВНЫЕ ПОНЯТИЯ Прежде чем перейти к детальному рассмотрению моделей печных процессов и методов моделирования этих процессов, введем некоторые обобщенные понятия, которые будут полезны для анализа и сравнения результатов математического моделирования. Это классификация моделей, их свойства или характеристики, а также стандартный подход к построению и реализации моделей на ЭВМ. Структура модели печи Независимо от уровня сложности модели и наличия того или другого числа микро- и макромодулей, модель печи укрупнено состоит из трех состыкованных между собой суперблоков, получивших названия: материальный баланс, энергетический баланс и тепломассообмен [1]. Суперблоки начиняются микро- и макромодулями в зависимости от сложности модели. Пример стандартной конфигурации суперблоков дан на рис. 3.1. Взаимодействие отдельных суперблоков и модулей осуществляется через информационные связи (математические зависимости) между отдельными параметрами (температуры, расходы, давления и т.д.). Связи могут быть односторонними и двусторонними. Примером двусторонних связей является ситуация, когда результаты расчета горения топлива используются для расчета температуры газа через граничные условия, а температура газов, в свою очередь, влияет на результаты расчета неполного горения топлива. Односторонней связью является, например, влияние результатов расчета окисления металла на расчет расхода топлива. Обратной реально ощутимой связи в данном случае нет. Необходимо помнить, что каждый из указанных на рис. 3.1 макромодулей, в свою очередь, может состоять из набора микро- и макромодулей более мелких процессов. Одной из важнейших стратегических задач, стоящих между учеными-теплотехниками, является создание микромодулей всех печных процессов. Это позволит в будущем создать универсальный набор модулей для любой конфигурации суперблоков.
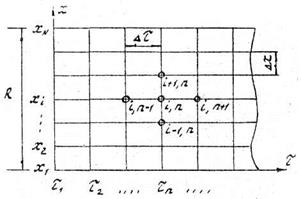
Рис. 3.1. Структура суперблоков модели печи 3.2. Основные принципы построения суперблока "Тепломассообмен" Суперблок "Тепломассообмен" является самым сложным при практической реализации. Это связано с тем, что нет высокоэкономичных методов для расчета таких процессов, как: · движение газов в рабочем пространстве печи (модуль "Расчет скоростей и давлений"). · процессы теплогенерации в рабочем пространстве печи или непосредственно в нагреваемом материале (Модуль "Расчет внутренних источников тепла") и других процессов. Немало трудностей таит в себе и расчет лучистого теплообмена в рабочем пространстве печи в сочетании с расчетом нагрева материала, особенно в нелинейных постановках задач. В реальных условиях не удается полностью охватить в единой модели все теплообменные процессы, в связи с чем выделяют наиболее существенные процессы в зависимости от конкретной задачи. В одних случаях требуется точно рассчитать температурное поле по сечению материала, в других – граничные условия на поверхности материала и т.д. Поэтому условно тепловые модели печных процессов разделяют на: модели внутреннего, внешнего и сопряженного теплообмена. Дадим краткую характеристику процессов, включаемых в эти модели. Внутренним теплообменом в теплотехнике называют процесс распространения теплоты в нагреваемом материале. Задача внутреннего теплообмена формулируется обычно в виде дифференциального уравнения теплопроводности с соответствующими краевыми условиями (см. разд. 5). Также в рамках внутреннего теплообмена рассматриваются нагрев термически тонких тел (разд. 4) и стационарная теплопроводность (разд. 6). Решение задач внутреннего теплообмена осуществляется, в основном, численными методами (метод конечных разностей, метод Эйлера и т.п.). Внешним теплообменом обычно называют процессы, проходящие в рабочем пространстве печи за пределами объема нагреваемого материала. Внешний теплообмен включает в себя, главным образом, конвекцию и излучение. Для расчета лучистого теплообмена чаще всего используется зональный метод, позволяющий свести интегро-дифференциальные уравнения переноса излучения к системам простых алгебраических уравнений. Для расчета конвективного переноса теплоты требуется составлять модель турбулентного движения газов и горения топлива в потоке. Эти модели основаны на дифференциальных уравнениях Навье-Стокса, уравнениях неразрывности и уравнениях энергии. Эти уравнения и им подобные переводятся в алгебраические за счет применения метода конечных разностей. Печь, как сложная система, может быть представлена в виде отдельных элементов, в которых реализуются разные процессы передачи теплоты (теплопроводность, конвекция, излучение). Эти процессы взаимосвязаны и носят название сопряженного теплообмена. Модели сопряженного теплообмена имеют наибольшее практическое значение для печей, т.к. включают в себя модели внутреннего и внешнего теплообмена. Сопряжение идет через граничные условия. Именно такие модели позволяют в комплексе оценить работу печей и позволяют проводить многовариантные оптимизационные расчеты. Основные понятия теории разностных схем Основная идея метода конечных разностей заключается в том, что непрерывная область изменения пространственной и временной переменных заменяется конечным числом дискретно расположенных узловых точек: по пространству: и по времени: Расстояние между узлами называется шагом. Например, Для случая одномерной задачи набор узловых точек представлен на рис. 5.1. Такая система узловых точек, соединенных между собой, называется разностной сеткой. Каждый узел сетки имеет свои координаты (i, n) или ( Если шаг сетки по пространству и по времени равномерный, то текущие значения координат определяются из соотношений
Рис. 5.1. Разностная сетка для одномерной задачи теплопроводности
Для неравномерной сетки шаг по времени и пространству может изменяться произвольным образом. Этот случай мы не рассматриваем. Покажем как перейти от производной к ее алгебраическому аналогу, используя разностную сетку. По определению производной, если есть непрерывная и дифференцируемая функция, то ее производная будет равна
где Таким образом, производная определяется параметрами в соседних, достаточно близких, точках (узлах) пространства. Если принять, что
При аппроксимации производной величиной Существуют 3-и основных способа представления производных по пространству в точке i: разность "назад" (левая разность)
разность "вперед" (правая разность)
и центральная разность
Аппроксимируя производную по времени в точке "n", всегда берут разность "вперед" или разность "назад"
т.к. при использовании центральной разности расчет неустойчив. Вторую производную чаше всего представляют в виде:
Такие понятия, как погрешность численного решения ( Так, разности "вперед" и "назад" (5.4, 5.5, 5.7) имеют погрешность, пропорциональную соответствующему шагу в 1-я степени (1-й порядок точности), а центральная разность (5.6) – шагу во 2-й степени (2-й порядок точности). Аппроксимация второй производной в виде (5.8) также имеет 2-й порядок точности. Метод прогонки Метод прогонки является самым экономичным методом для решения систем уравнений подобных (5.13). Представим (5.13) в следующем формализованном виде:
где Здесь индексы (n+1) опущены для простоты записи. В уравнении (5.14) только три неизвестные:
где для N равного, например, 5
Матрица коэффициентов Теперь предположим, что между температурами в соседних узлах существует линейная зависимость
где Подставив (5.15) в (5.14), получим уравнение с двумя неизвестными
Отсюда в виде линейной зависимости легко выражается
т.е. предположение (5.15) подтвердилось. Из аналогии (5.17) и (5.15) можно найти коэффициенты
Коэффициенты ai и bi называются прогоночными коэффициентами и они находятся во всех узлах разностной сетки по рекуррентным формулам (5.18) и (5.19). Порядок решения систем уравнений, подобных (5.14), следующий: сначала определяются из граничных условий коэффициенты a1 и b1. Затем по выражениям (5.18) и (5.19) коэффициенты a2, b2; a3, b3 и т.д. до aN-1, bN-1. Эта часть алгоритма называется прямой прогонкой. Далее из граничных условий на противоположной границе находится температура tN и по формуле (5.15) обратной прогонкой последовательно определяются температуры в узлах сетки от (N-1) до 1:
Преимущества метода прогонки перед другими методами – экономичность. Это означает, что при расчетах по этому методу требуется выполнить минимальное число арифметических операций. Например, по методу Гаусса число операций Локально-одномерная схема Локально-одномерная схема позволяет свести уравнение (5.33) к двум одномерным уравнениям: а) по направлению х:
б) по направлению у:
Порядок расчета по этой схеме следующий: 1. Сначала находится значение фиктивной температуры 2. Далее, исходя из известного поля фиктивных температур Несколько коротких характеристик схемы: а) она самая экономичная из известных на сегодняшний день схем, имеющих погрешность б) схема является сходящейся и безусловно устойчивой. Продольно-поперечная схема Данная схема родилась из локально-одномерной с целью увеличения скорости сходимости последней. Подход к ее формированию напоминает подход, изложенный в схеме Кранка-Николсона для одномерных задач. Продольно-поперечная схема представляет из себя аппроксимацию уравнения теплопроводности в следующем виде: а) по направлению "х":
при i = 2,3,...,N-1; j = 1,2,...,M.
б) по направлению "у":
при j = 2,3,...,M-1; i = 1,2,...,N.
Последовательность расчета та же, что и для реализации локально-одномерной схемы. Схема является безусловно устойчивой.
Погрешность схемы ~ Явная разностная схема Явная схема обычно представляется в виде
где n= 0, 1,... – номер итерационного шага; w – итерационный параметр. Особенность явной схемы в том, что температура в процессе итерационного счета выражается в явном, достаточно простом виде без решения систем уравнений. Явная схема устойчива при w £ 1. Последовательность расчета температурного поля приведена на блок-схеме рис.6.2. В блоке 4 формула (6.7) приведена условно, поскольку она справедлива только для внутренних узлов сетки. Естественно, что для граничных узлов должны быть использованы другие формулы (см. разд.6.4).' Основная сложность расчета заключается в выборе итерационного параметра "w". От него зависит сходимость решения. Самая низкая скорость при w = 1. Этот случай известен под названием метод Якоби. Однако на практике схема (6.7) используется редко из-за своих недостатков: – низкая скорость сходимости; – узкие пределы варьирования итерационного параметра; – необходимость при расчетах на ЭВМ пользоваться двумя массивами температур
Рис. 6.2. Логическая блок-схема для расчета стационарного температурного поля по явной схеме
Этих недостатков лишена явная схема Зейделя, в соответствии с которой имеем
Здесь предполагается, что Неявная разностная схема Неявная разностная схема выводится из того положения, что стационарное температурное поле является установившимся случаем нестационарного поля при бесконечно большом времени протекания процесса нагрева. При. этом итерационный параметр "w" играет роль шага по времени в эквивалентном уравнении теплопроводности:
при i = (2, 3,..., N-1) и j = (2, 3,..., M-1) (рис.6.1б). Для того, чтобы определить температуру на (n+1)-й итерации, надо решить систему уравнений типа (6.9), записанных для каждого внутреннего узла разностной сетки, плюс набор уравнений для граничных узлов. В целом получается система (N M)- уравнений с (N M)- неизвестными температурами. Причем, матрица связанных коэффициентов перед температурами – пятидиагональная. Такую систему линейных алгебраических уравнений надо решать или методом исключения Гаусса или методом обращения матриц или итерационным методом, т.е. методами, которые требуют значительного количества арифметических операций при реализации на ЭВМ. В попытке отойти от этих неэкономичных методов возникли модификации неявной схемы, которые по аналогии с решением многомерных нестационарных задач теплопроводности разделили на локально-одномерную и продольно-поперечную схемы. Эти схемы позволяют свести указанные системы уравнений к системам с трехдиагональными матрицами связанных коэффициентов и, в конечном счете, позволяют применить метод прогонки решения системы уравнений. На практике целесообразно применять продольно-поперечную схему, обладающую наиболее высокой скоростью сходимости. Эта схема записывается в виде 2-х уравнений: по направлению х:
при i = (2, 3, …, N-1) и по направлению у:
при j = (2, 3,..., M-1). Алгоритм решения задачи по этой схеме приведен на рис.6.3.
Рис. 6.3. Логическая блок-схема расчета стационарного температурного поля по неявной схеме
Особенность алгоритма состоит в расчете промежуточного значения температуры на (n+1/2) итерационном шаге, которая является исходной для окончательного расчета на (п+1)-м шаге. Для указанной выше неявной схемы итерационный параметр "w" может принимать произвольное значение. Его можно подобрать таким, что резко будет увеличена скорость сходимости, т.е. решение будет получено за минимальное число итераций. ЛИТЕРАТУРА 1. Высокотемпературные теплотехнологические процессы и установки / Перелетов И.И., Бровкин Л.А., Розенгарт Ю.И. и др. Под ред. А.Д. Ключникова - И.: Энергоатомиздат, 1989. - 336 с. 2. Арутюнов В.А., Бухмиров В.В., Крупенников С.А. Математическое 3. Расчеты нагревательных печей. / Аверин С.И. и др. Под ред. Н.Ю.Тайца - Киев: Техника, 1969. - 540 с. 4. Расчет нагревательных и термических печев: Справ. изд. / Василькова С.Б. и др. Под ред. В.М. Тымчака и В.Л. Гусовского - М.: Металлургия. 1983. - 480 с. 5. Абраменков Ю.Я. Топливо, огнеупоры и металлургические печи. Ч.1. Расчеты горения и теплотехническая оценка топлива. Учеб. пособие. - К.: УМК ВО, 1991. - 88 с. 6. Губинский В.И., Минаев А.Н., Гончаров Ю.В. Уменьшение окалинообразования при производстве проката. К.: Техника, 1981. - 135 с. 7. Лисиенко В.Г. Интенсификация теплообмена в пламенных печах. -М.: Металлургия, 1979. - 224 с. 8. 1973,.18, №1, Р.25-40. 9. Ши Д. Численные методы в задачах теплообмена.: Пер. с англ. - М.: Мир, 1988. - 544 с. 10. Свинолобов Н.П., Абраменков Ю.Я. Методы численного решения и математического моделирования процессов теплопроводности. Учеб. пособие. - Днепропетровск: ДМетИ. 1974. - 77 с. 11. Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. - М.: Энергоатомиздат, 1984. - 150 с. 12. Методические указания к выполнению лабораторных и практических работ по дисциплине "Элементы теории систем и численные методы моделирования тепломассопереноса" для студентов специальности 11.03 "Теплофизика, автоматизация и экология тепловых агрегатов в металлургии".- Днепропетровск: ДМетИ. 1992. - 38 с. 13. Блох А.Г., Журавлев Ю.А., Рыжков Л.Н. Теплообмен излучением: Справочник. - И.; Энергоатомиздат, 1991. - 432 с. 14. К определению угловых коэффициентов излучения между прямоугольниками различных размеров / Чеховский И.Р. и др./ Теплофизика высоких температур, т.17, 1979, №1. С. 116-119. 15. Дульнев Г.Н., Парфенов В.Г., Сигалов А.В. Применение ЭВМ для решения задач теплообмена. - М.: Высшая школа, 1990. - 207 с. 16. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. - М.: Энергоиздат, 1981. - 416 с. 17. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся вузов. - М.: Наука. 1981. - 720 с. 18. Годунов С.К., Рябенький В.С. Разностные схемы (введение в теорию). - М.: Наука, 1977. - 439 с. 19. Налимов В.В., Чернова Н.А. Статистические методы планирования экстремальных экспериментов. - М.: Наука, 1965. - 340 с. 20. Тепло- и массообмен. Теплотехнический эксперимент: Справочник / Аметистов Е.В. и др.; Под общ. ред. В.А. Григорьева и В.М. Зорина - М.: Энергоиздат, 1982. - 512 с. СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 3 1. МЕТОДЫ ИССЛЕДОВАНИЯ РАБОТЫ ПЕЧЕЙ.. 5 1.1. Экспериментальный метод исследований. 5 1.2. Стохастическое моделирование. 5 1.3. Физическое моделирование. 6 1.4. Математическое моделирование. 6 2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТЕПЛООБМЕНА В ПЕЧИ. ОСНОВНЫЕ ПОНЯТИЯ 8 2.1. Классификация математических моделей. 8 2.2. Рабочие характеристики математических моделей. 9 2.3. Основные этапы решения задач методом математического моделирования 11 3. БЛОЧНО-МОДУЛЬНЫЙ ПОДХОД К ПОСТРОЕНИЮ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ.. 13 3.1. Структура модели печи. 13 3.2. Основные принципы построения суперблока "Тепломассообмен". 14 4. ОСНОВНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА НАГРЕВА В ПЕЧИ ТЕРМИЧЕСКИ ТОНКИХ ТЕЛ.. 16 4.1. Общие понятия численных методов при моделировании нагрева ТТТ. 17 4.2. Простейшие численные методы решения О.Д.У. 19 4.3. Погрешность аппроксимации по схеме Эйлера. 23 4.4. Схемы Эйлера высокого порядка аппроксимации. 24 4.5. Устойчивость разностной схемы Эйлера. 24 5. КОНЕЧНО-РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ТЕПЛОПРОВОДНОСТИ (НАГРЕВ ТЕРМИЧЕСКИ МАССИВНЫХ ТЕЛ) 26 5.1. Основные понятия теории разностных схем. 26 5.2. Аппроксимация уравнения теплопроводности по явной схеме. 28 5.2.1. Обоснование условия устойчивости явной схемы.. 29 5.3. Неявная конечно-разностная схема. 30 5.3.1. Метод прогонки. 30 5.4. Погрешность разностной аппроксимации. 32 5.5. Комбинированная разностная схема (схема Кранка-Николсона) 34 5.6. Многомерные задачи теплопроводности. 34 5.6.1. Локально-одномерная схема. 36 5.8.2. Продольно-поперечная схема. 37 5.7. Аппроксимация граничных условий. 38 5.7.1. Схемы 2-го порядка аппроксимации по методу теплового баланса 38 5.7.2. Схемы 1-го порядка аппроксимации (метод восстановления) 40 5.7.3. Схемы 2-го порядка аппроксимации по методу неопределенных коэффициентов. 41 5.8. Решение нелинейных задач теплопроводности. 42 6. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ ДЛЯ РАСЧЕТА СТАЦИОНАРНОГО ТЕМПЕРАТУРНОГО СОСТОЯНИЯ ЭЛЕМЕНТОВ ПЕЧИ.. 44 6.1. Основные численные соотношения. 44 6.2. Явная разностная схема. 46 6.3. Неявная разностная схема. 47 6.4. Аппроксимация граничных условий. 49 7. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН В ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ 51 7.1. Конечно-разностная аппроксимация уравнений движения и неразрывности 53 7.2. Конечно-разностная аппроксимация уравнения энергии. 55 7.2.1. Условие устойчивости неявной схемы уравнения энергии. 56 7.3. Аппроксимация граничных условий. 56 7.4. Учет турбулентности пограничного слоя. 57 8. МЕТОДЫ РАСЧЕТА ДВИЖЕНИЯ ГАЗОВ В ОБЪЕМЕ ПЕЧИ.. 59 8.1. Основные соотношения, описывающие движение газов в замкнутом объеме 59 8.2. Конечно-разностные методы расчета в переменных "функция тока-завихренность". 60 8.2.1. Аппроксимация граничных условий. 62 8.3. Методы расчета движения газов в переменных "скорость-давление". 63 8.3.1. Экономичный алгоритм Патанкара. 66 9. ЧИСЛЕННЫЕ МЕТОДЫ МОДЕЛИРОВАНИЯ ЛУЧИСТОГО ТЕПЛООБМЕНА В РАБОЧЕМ ПРОСТРАНСТВЕ ПЕЧИ.. 68 9.1. Зональный метод расчета стационарного теплообмена в системе тел с диатермичной средой. 69 9.2. Резольвентно-зональный метод расчета лучистого теплообмена в замкнутой системе тел. 71 10. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ 3-ГО УРОВНЯ СЛОЖНОСТИ НАГРЕВАТЕЛЬНЫХ ПЕЧЕЙ.. 74 10.1. Математическая модель сопряженного теплообмена в печи с шагающим подом 74 10.2. Алгоритм расчета теплообмена по модели. 76 10.3. Расчет коэффициентов поглощения и степеней черноты продуктов горения 77 10.4. Расчет угловых коэффициентов. 79 11. ПРОВЕРКА АДЕКВАТНОСТИ И АДАПТАЦИЯ МОДЕЛЕЙ.. 80 11.1. Математическая модель нагрева металла в камерной печи. 82 11.1.1. Процедура адаптации по результатам замера температуры в процессе нагрева. 83 11.1.2. Процедура адаптации на основе замеров температуры металла в конце нагрева. 84 ЛИТЕРАТУРА.. 86
ВВЕДЕНИЕ Данное учебное пособие составлено на основе опыта преподавания автором таких дисциплин, как "Моделирование печей и их элементов", "Элементы теории систем и численные методы моделирования тепломассопереноса" и "Применение ЭВМ для моделирования и оптимизации промышленных печей". Объем учебного пособия рассчитан на 28-36 часов лекции и предназначен для студентов 3-4 курсов. Считается, что читатель знаком с общими закономерностями теплообменных процессов, происходящих в печи. Теперь же надо научиться использовать эти закономерности для получения конкретных численных (числовых) значения показателей работы печей. Одна из целей представленных ниже материалов: научиться прогнозировать температуры, тепловые потоки, скорости и расходы теплоносителей в любом тепловом агрегате и, тем более, в печи. Такой прогноз мы будем давать путем моделирования, причем, моделирования на основе ЭВМ. Моделирование – это процесс создания и использования моделей, имитирующих работу какого-либо объекта. В свою очередь, модель можно определить так: "модель – это объект, созданный для воспроизведения некоторого другого объекта, называемого натурой" [1]. Основные затруднения, связанные с моделированием работы печей возникают при учете множества взаимосвязанных сложных печных процессов. В таких сложных объектах, как печи, всегда присутствуют вероятностные и детерминированные процессы. Вероятностные процессы обычно вызваны постепенным износом агрегата в процессе эксплуатации и соответственным изменением его характеристик, а также квалификацией обслуживающего персонала. Наличие вероятностных процессов затрудняет сравнение результатов моделирования с реально существующими показателями печей. Детерминированные процессы – это процессы и связи, действующие в любой ситуации четко определенным образом. Моделирование работы печей на ЭВМ направлено, главным образом, для исследования детерминированных процессов, но существуют отдельные виды моделирования или методы исследования, позволяющие учитывать и вероятностный характер работы печей. Настоящая работа состоит из 11 больших разделов, расположенных в логической последовательности: сначала даются общие положения (разд. 1 и 2), затем разбирается структурный подход к разработке моделей печей (разд. 3), описываются методы расчета теплообмена в рамках отдельных суперблоков общей структуры (разд. 4-9) и приводится пример построения математической модели (разд. 10). При моделировании теплообмена мы исходим из того, что разработка модели не является самоцелью. Модель должна быть приспособлена для практических расчетов и поэтому в работе отдельно выделены вопросы проведения процедуры адаптации модели по экспериментальным данным (разд. 11). Необходимо кратко пояснить структуру материалов, представленных в разделах 4-9. Во-первых, мы ограничились задачами, позволяющими в полной мере рассчитать теплообмен и оценить тепловую работу только пламенных нагревательных и термических печей. Опущены такие большие разделы, как плавление материалов, теплообмен в слое материалов, нагрев металла в инд
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 673; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.694 с.) |




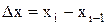 – шаг по координате,
– шаг по координате, 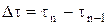 – шаг по времени.
– шаг по времени. ), при которых определяется температура.
), при которых определяется температура. ; (5.1)
; (5.1) .
.
 , (5.2)
, (5.2) – изменение функции, соответствующее малому приращению координаты –
– изменение функции, соответствующее малому приращению координаты – 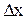 ;
; 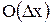 – малая величина, имеющая порядок
– малая величина, имеющая порядок  ..(5.3)
..(5.3)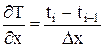 (5.4)
(5.4) (5.5)
(5.5) (5.6)
(5.6) или
или  , (5.7)
, (5.7)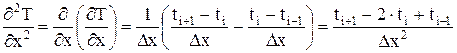 . (5.8)
. (5.8) ), разностная схема, сходимость, устойчивость схем, порядок точности и другие, описанные в разделе 4, сохраняются и при использовании метода конечных разностей для аппроксимации дифференциальных уравнении в частных производных.
), разностная схема, сходимость, устойчивость схем, порядок точности и другие, описанные в разделе 4, сохраняются и при использовании метода конечных разностей для аппроксимации дифференциальных уравнении в частных производных. при
при  (5.14)
(5.14)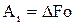 ;
; 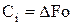 ;
;  ;
;  ;
;  .
.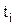 ,
,  ,
,  . Это определяет специфический вид матрицы связанных коэффициентов в системе уравнений (5.14). В матричной форме система уравнений имеет вид
. Это определяет специфический вид матрицы связанных коэффициентов в системе уравнений (5.14). В матричной форме система уравнений имеет вид ,
, ;
;  ;
; 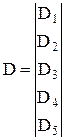 .
. , (-Bi) и Ci носит название разреженной 3-х диагональной, поскольку она заполнена нулями кроме 3-х главных диагоналей. В этом, кстати, ограниченность метода прогонки: он может применяться при решении систем уравнений только с 3-х диагональной матрицей связанных коэффициентов.
, (-Bi) и Ci носит название разреженной 3-х диагональной, поскольку она заполнена нулями кроме 3-х главных диагоналей. В этом, кстати, ограниченность метода прогонки: он может применяться при решении систем уравнений только с 3-х диагональной матрицей связанных коэффициентов.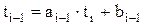 , (5.15)
, (5.15) и
и 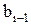 – некоторые коэффициенты.
– некоторые коэффициенты. . (5.16)
. (5.16) , (5.17)
, (5.17) и
и 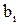 :
: ; (5.18)
; (5.18) (5.19)
(5.19) ;
;  ; …;
; …;  ; …
; …  .
. , а по методу прогонки
, а по методу прогонки 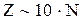 . Так, если число узлов по сечению тела N = 100, то по методу Гаусса получим порядка 1 000 000 арифметических действий, а по методу прогонки – всего 1 000.
. Так, если число узлов по сечению тела N = 100, то по методу Гаусса получим порядка 1 000 000 арифметических действий, а по методу прогонки – всего 1 000.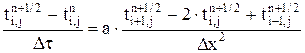 (
(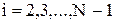 ;
; 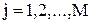 ). (5.34)
). (5.34) (
(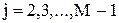 ;
; 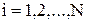 ). (5.35)
). (5.35)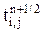 на промежуточном (n+1/2) шаге по времени. Для этого методом прогонки решается система уравнений подобных (5.34) совместно с граничными условиями по направлению "х".
на промежуточном (n+1/2) шаге по времени. Для этого методом прогонки решается система уравнений подобных (5.34) совместно с граничными условиями по направлению "х".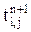 . Для этого методом прогонки решается система уравнений (5.35), записанных по направлению "у". Естественно, что в систему уравнений должны быть включены два уравнения из граничных условий (при j = 1 и при j = N).
. Для этого методом прогонки решается система уравнений (5.35), записанных по направлению "у". Естественно, что в систему уравнений должны быть включены два уравнения из граничных условий (при j = 1 и при j = N).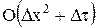 ;
;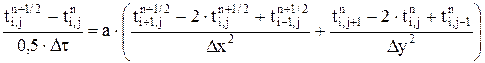 (5.36)
(5.36)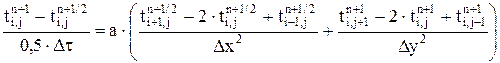 (5.37)
(5.37) . Если сравнивать локально-одномерную и продольно-поперечную схемы по экономичности расчета на одном шаге по времени, то локально-одномерная более эффективна. Но если принимать во внимание требуемое число шагов по времени и соответствующее числу шагов число арифметических операций для достижения одинаковой точности результатов, то продольно-поперечная схема имеет несомненные преимущества.
. Если сравнивать локально-одномерную и продольно-поперечную схемы по экономичности расчета на одном шаге по времени, то локально-одномерная более эффективна. Но если принимать во внимание требуемое число шагов по времени и соответствующее числу шагов число арифметических операций для достижения одинаковой точности результатов, то продольно-поперечная схема имеет несомненные преимущества. , (6.7)
, (6.7) (на шаге "n" и на шаге "n+1").
(на шаге "n" и на шаге "n+1").
 . (6.8)
. (6.8) , и
, и  уже известны. Схема Зейделя гораздо эффективнее обычной явной схемы. Она устойчива при 0 £ w £ 2. Когда w<1, то расчет осуществляется методом последовательной нижней релаксации (ПНР), а когда 1 < w £ 2, то расчет носит название метод последовательной верхней релаксации (ПВР). Метод ПВР обычно позволяет достичь более высокой скорости сходимости. Рекомендуется принимать w=1,6¸1,8 для минимизации числа итерационных шагов.
уже известны. Схема Зейделя гораздо эффективнее обычной явной схемы. Она устойчива при 0 £ w £ 2. Когда w<1, то расчет осуществляется методом последовательной нижней релаксации (ПНР), а когда 1 < w £ 2, то расчет носит название метод последовательной верхней релаксации (ПВР). Метод ПВР обычно позволяет достичь более высокой скорости сходимости. Рекомендуется принимать w=1,6¸1,8 для минимизации числа итерационных шагов.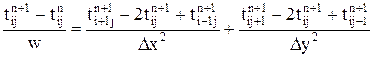 (6.9)
(6.9) (6.10)
(6.10) (6.11)
(6.11)



