
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидродинамический и тепловой пограничные слоиСодержание книги
Поиск на нашем сайте На плоской пластине
Рассмотрим поток, обладающий неизменными теплофизическими характеристиками (r, m, l, cp = const), совершающий вынужденное движение вдоль плоской полубесконечной тонкой пластины и обменивающейся с ней теплом. Предположим, что неограниченный поток со скоростью Выделим гидродинамический и тепловой пограничные слои Проанализируем уравнения неразрывности и Навье-Стокса. Задача двухмерная, поскольку wz,
Как известно «х» dг, поэтому Следовательно, имеем
Записывать аналогичные уравнения для оси у не имеет смысла, так как wy может быть найдена из уравнения неразрывности (22). Используя аналогичные процедуры можно упростить и уравнение Фурье-Кирхгофа
Система дифференциальных уравнений (22)–(24) составляет изотермическую математическую модель плоского стационарного теплового ламинарного пограничного слоя. Сформулируем граничные условия Итак, граничные условия:
w x (x, 0) = 0, x > 0; wx (x, ∞) = T (x, 0) = T ст, x > 0; T (x, ∞) = T °; T (0, y) = T °. (26)
Точное решение этой задачи в виде бесконечных рядов было получено Блазиусом. Имеются более простые приближенные решения: метод интегральных соотношений (Юдаев) и теорема импульсов (Шлихтинг). А.И. Разиновым задача была решена методом сопряженного физического
Pr = ν/a.
Коэффициент А в формуле (27) у Разинова – 5,83; Юдаева – 4,64; Блаузиуса – 4; Шлихтинга – 5,0. Примерный вид найденных зависимостей приведен на рис. 1.3. Как известно, для газов Pr ≈ 1, капельных жидкостей Pr > 1. Полученные результаты позволяют определить коэффициенты импульса и теплоотдачи. Локальные значения γ(x) и Nu г, x
Рис. 1.3. Гидродинамический и тепловой ламинарные пограничные слои на плоской пластине
Усредненные значения
Аналогично для теплоотдачи
В данном случае аналогия тепло- и импульсоотдачи сохраняется (исходные уравнения одинаковы, граничные условия подобны). Критерий, характеризующий гидродинамическую аналогию процесса теплоотдачи имеет вид
Pт-г, x = Nu т, x / Nu г, x = Pr 1/3. (33)
Если Pr = 1, то Pт-г, x = 1, следовательно полная аналогия процессов импульсо- и теплоотдачи. Из полученных уравнений следует
γ ~
Как правило, подобная качественная зависимость выполняется Задача рассматривается в изотермической постановке, тепловые граничные условия первого рода Т ст = const. По мере удаления от кромки пластины (увеличения координаты х) происходит рост dг(х). При этом неоднородность поля скорости wx распространяется в области все более удаленные от границы раздела фаз, Толщина же всего турбулентного теплового пограничного слоя обычно определяется из условия ν т = ат, следовательно dг = dт. Сначала рассмотрим турбулентный гидродинамический пограничный слой (рис. 1.4). Оставим в силе все приближения, сделанные для ламинарного слоя. Единственное отличие – наличие νт (у), поэтому
Сохраним и граничные условия. Решением системы уравнений (35)
Рис. 1.4. Гидродинамический и тепловой турбулентные пограничные слои на плоской пластине
Как и в случае ламинарного пограничного слоя возможно использование осредненных по длине l коэффициентов импульсоотдачи
Рассмотрим тепловой турбулентный пограничный слой. Уравнение энергии имеет вид
Если Pr > 1, то внутри вязкого подслоя можно выделить тепловой подслой, где молекулярный перенос тепла
Для локального коэффициента теплоотдачи решение математической модели имеет вид
Среднее по длине пластины значение
Ниже представлены образование турбулентного пограничного слоя (а) и распределение локального коэффициента теплоотдачи (б) при продольном обтекании плоской полубесконечной пластины (рис. 1.5).
Рис. 1.5. Пограничные слои dг и dт и локальный коэффициент теплоотдачи a на плоской пластине
В ламинарном слое (х ≤ l кр) тепловой поток только за счет теплопроводности, для качественной оценки можно использовать соотношение a ~ В переходной зоне общая толщина пограничного слоя увеличивается. Однако значение a при этом увеличивается, потому что толщина ламинарного подслоя уменьшается, а в образующемся турбулентном слое тепло переносится не только теплопроводностью, но и конвекцией вместе Итак, рассмотрены гидродинамический и тепловой пограничные слои на плоской пластине. Качественный характер полученных зависимостей справедлив и для пограничных слоев, образующихся при обтекании более сложных поверхностей.
Теплообмен в круглой трубе
Рассмотрим стационарный теплообмен между стенками горизонтальной прямой трубы круглого сечения и потоком, обладающим неизменными теплофизическими характеристиками и движущимся за счет вынужденной конвекции внутри нее. Примем тепловые граничные условия первого рода, т.е. Т ст = const. I. Участки гидродинамической и термической стабилизации. При входе жидкости в трубу за счет торможения, вызываемого стенками, на них формируется гидродинамический пограничный слой. Подобно изменению профиля скоростей по длине трубы изменяется II. Рассмотрим ламинарное движение жидкости. Ранее, в разделе дисциплины «Гидродинамика и гидродинамические процессы» [2], нами был рассмотрен гидродинамический начальный участок. Для определения длины начального участка была предложена следующая зависимость
Для жидкости Pr > 1, следовательно, тепловой пограничный слой будет находиться внутри гидродинамического пограничного слоя. Температура жидкости во входном сечении теплообменного участка постоянна по сечению и равна Т ° и в ядре потока она не меняется. При этих условиях уравнение теплового пограничного слоя имеет вид
Решение этого уравнения при вышеперечисленных условиях дает: · для длины теплового начального участка
· для местного коэффициента теплоотдачи
· для среднего коэффициента теплоотдачи длиной
· для местного числа Нуссельта
· для среднего числа Нуссельта
Рассмотрим уравнение (42). Если
Рис. 1.6. Профиль температуры на начальном и стабилизированном участке при ламинарном течении жидкости в цилиндрической трубе
При турбулентном течении потока в трубе, как и на плоской пластине, во-первых, толщины гидродинамического и теплового пограничных слоев совпадают; а во-вторых, растут значительно быстрее, чем для ламинарных. Это приводит к уменьшению длины участков термической
III. Стабилизированный теплообмен при ламинарном движении среды. Рассмотрим стационарный теплообмен в круглой трубе, когда теплофизические свойства жидкости постоянны (изотермический случай), профиль скорости не меняется по длине, температура стенки трубы постоянна и равна Т ст, в потоке отсутствуют внутренние источники тепла,
Граничные условия:
Решение этой задачи впервые было получено Гретцем, затем Нуссельтом, в виде суммы бесконечного ряда. Несколько иное решение было получено Шумиловым и Яблонским. Полученное решение справедливо Для области стабилизированного теплообмена локальный коэффициент теплоотдачи равен предельному
Как видно из рисунка (рис. 1.7), с увеличением
Рис. 1.7. Изменение местного IV. Стабилизированный теплообмен при турбулентном движении среды. Исходное уравнение
Граничные условия:
При решении задачи возникает проблема выбора профиля скорости wx. Одни для wx используют логарифмический закон (А.И. Разинов), другие – закон 1/7 (В.Б. Коган). Отмечается консервативность турбулентных течений, которая заключается в слабом влиянии граничных условий и поля скорости wx на коэффициенты теплоотдачи. Для числа Нуссельта предлагается следующая формула
Как и для ламинарного движения в области стабилизированного теплообмена при турбулентном течении среды Nu не зависит от координаты х. Нами был рассмотрены выше частные случаи теплообмена, а именно: при изотермической постановке задачи и тепловых граничных условиях первого рода теплообмен в гладких цилиндрических трубах и плоских горизонтальных пластинах. В литературе имеются решения тепловых задач и для других случаев. Отметим, что шероховатость поверхности трубы и пластины ведет
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 675; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

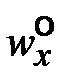
 и Т ° постоянны.
и Т ° постоянны. . По экспериментальным данным известно, что в гидродинамическом пограничном слое
. По экспериментальным данным известно, что в гидродинамическом пограничном слое  . В ядре потока
. В ядре потока  const, поэтому, согласно уравнению Бернулли
const, поэтому, согласно уравнению Бернулли 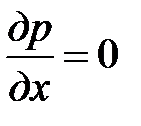 , в пограничном слое то же самое
, в пограничном слое то же самое .
. .
. ; (22)
; (22) . (23)
. (23) . (24)
. (24) . Для поля температуры аналогичные рассуждения.
. Для поля температуры аналогичные рассуждения. ; wx (0, y) =
; wx (0, y) =  ; (27)
; (27)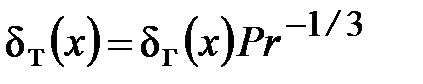 , Pr ≥ 1; (28)
, Pr ≥ 1; (28) ,
, 
 . (29)
. (29)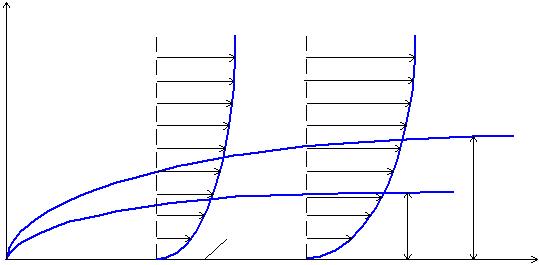

 и
и  по участку длиной l
по участку длиной l ,
, 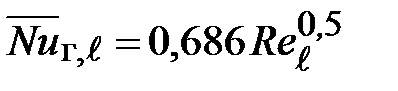 ,
,  . (30)
. (30) ,
,  ; (31)
; (31) ,
,  . (32)
. (32) , m; a ~
, m; a ~  . (35)
. (35)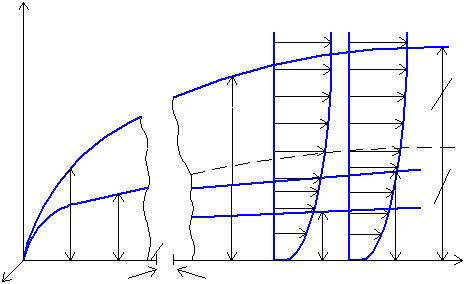


 . (36)
. (36) . (37)
. (37) . (38)
. (38) . (39)
. (39) определяется так
определяется так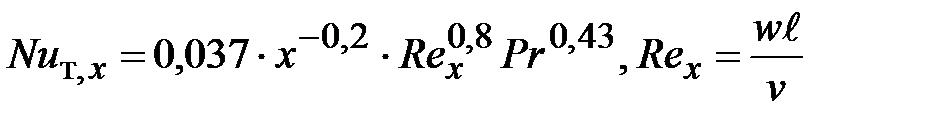 . (40)
. (40)

 .
. .
. .
. . (41)
. (41) ; (42)
; (42) ; (43)
; (43)
 ; (44)
; (44) ; (45)
; (45)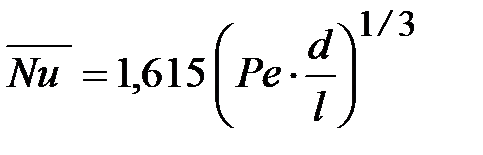 . (46)
. (46) , то
, то  .
. . (47)
. (47)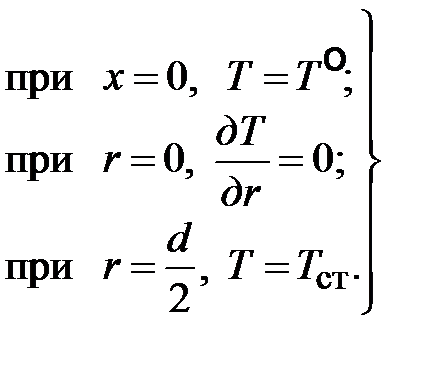 (48)
(48) или
или  (49)
(49) число Nu уменьшается, асимптотически приближаясь на втором участке кривой
число Nu уменьшается, асимптотически приближаясь на втором участке кривой

 и среднего Nu по длине круглой трубы при Т ст = const
и среднего Nu по длине круглой трубы при Т ст = const . (50)
. (50) (51)
(51)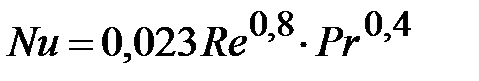 . (52)
. (52)


