
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кондуктивный теплообмен в цилиндрической стенкеСодержание книги
Поиск на нашем сайте
Исходное уравнение в цилиндрической системе координат r, j, z имеет вид
Считаем, что процесс теплообмена стационарный и длина цилиндра достаточно велика для того, чтобы пренебречь потоком тепла к его торцам вдоль оси z, процесс осесимметричный. При этих условиях температура является функцией только одной координаты – радиуса r (рис. 1.2):
или
Рис. 1.2. Распределение температуры в цилиндрической стенке Написав уравнение (12) в виде
и разделив переменные, получим
Выполняя интегрирование, находим
Положив, что С = lnC 1, где C 1 – некоторая новая постоянная, получим
Вторичное интегрирование дает
T = C 1 lnr + C 2. (13)
Постоянные интегрирования находим из граничных условий:
при при
Отсюда
Окончательно
Как видно из уравнения (14) имеет место логарифмический закон распределения температуры по радиусу цилиндра. Градиент температуры на внутренней поверхности цилиндра равен
В правой части уравнения для любого r в знаменателе вместо R 1 необходимо брать r. Поток тепла за счет теплопроводности определяется как
Как видно из уравнения (15) тепловой поток зависит от координаты r Количество теплоты находим как
Здесь F = 2p rL – внутренняя поверхность цилиндра, t – время, L – высота цилиндра. Расход тепла определяется как
Если труба многослойная и состоит из n слоев, тогда для потока тепла получим
Здесь ∆ T = T 1 – Tn – общая разница температуры. Зависимость q м и F от радиуса r не позволяет использовать традиционную форму уравнения теплопередачи для цилиндрической стенки. В этом случае используется коэффициент теплопередачи
Здесь Для тонкостенных цилиндров, к которым можно отнести большинство труб, без большой ошибки можно использовать зависимости для плоской стенки.
Конвективный теплообмен
При конвекции перенос теплоты происходит макрообъемными частицами потока теплоносителя. Конвекция всегда сопровождается теплопроводностью. Как известно, теплопроводность – явление молекулярное, конвекция – явление макроскопическое, при котором
Конвективный перенос теплоты описывается уравнением Фурье-Кирхгофа. Закономерности течения среды описываются уравнениями Навье-Стокса (ламинарный режим) и Рейнольдса (турбулентный режим), а также уравнением неразрывности. Исследование закономерностей конвективного теплообмена можно провести в изотермической и неизотермической постановке. В изотермической постановке сначала решаются уравнения Навье-Стокса и неразрывности, затем полученные значения скоростей используются для решения уравнения Фурье-Кирхгофа. Полученные таким способом значения коэффициентов теплоотдачи впоследствии уточняются, корректируются. В неизотермической постановке уравнения Навье-Стокса, неразрывности и Фурье-Кирхгофа решаются совместно, с учетом зависимости теплофизических свойств среды от температуры. В последнее время разработаны методы решения многих задач теплоотдачи в ламинарных потоках жидкости с учетом зависимости вязкости жидкости от температуры. Для турбулентных течений все сложнее. Однако можно использовать приближенные численные решения с помощью компьютерных технологий. Для решения этих уравнений необходимо поставить условия однозначности, которые включают начальные и граничные условия. Граничные условия теплообмена могут быть заданы различным способом: - граничные условия первого рода – задаются распределением температуры стенки:
простейший случай, когда Т cт = const; - граничные условия второго рода – задается распределение теплового потока на стенке
- граничные условия третьего рода – задается распределение температуры среды, окружающей канал и коэффициент теплоотдачи
Выбор вида граничного условия зависит от условий работы теплообменного оборудования.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.219.241 (0.008 с.) |

 . (11)
. (11) ;
; . (12)
. (12)


 .
. .
.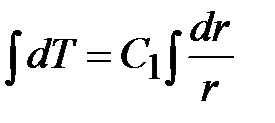 ;
;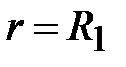
 ;
;  ;
;
 ;
;  .
. ; C 2 = T 1 - lnR 1.
; C 2 = T 1 - lnR 1. . (14)
. (14)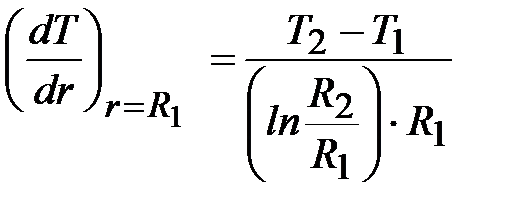 .
. . (15)
. (15)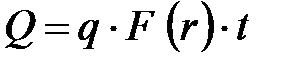 . (16)
. (16) . (17)
. (17) . (18)
. (18)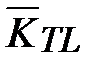 отнесенный
отнесенный ,
, 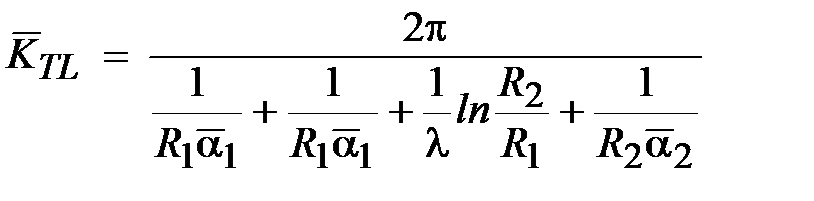 .
.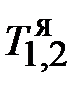 – температура в ядре фаз, омывающих цилиндрическую поверхность.
– температура в ядре фаз, омывающих цилиндрическую поверхность. l(Т)
l(Т) ; (19)
; (19) ; (20)
; (20) . (21)
. (21)


