Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Термодинамика состояния рабочих сред тепло- и массообменных аппаратов кондиционирования.Содержание книги
Поиск на нашем сайте
Термодинамика состояния рабочих сред тепло- и массообменных аппаратов кондиционирования. Расчет УКВ заключается в определении параметров состояния обменивающихся рабочих сред и потоков тепла и массы между ними. Рабочие среды в обменных аппаратах представляют собой гомогенные либо гетерогенные системы. Гомогенной называют такую систему, химический состав и физические свойства которой во всех частях одинаковы и изменяются непрерывно без скачка от одной точки системы к другой. Гетерогенной называется система, состоящая из двух и более различных гомогенных областей. Гомогенные области в гетерогенной системе являются компонентами или фазами различных компонентов системы. После разделения гетерогенной системы на компоненты и фазы ее можно полностью термодинамически описать. В термодинамике принят ряд характеристических функций, определяющих состояние отдельных компонентов и фаз. С помощью этих функций могут быть в явной форме выражены все термодинамические свойства состояния компонентов. Выбор тех или иных функций для расчетов определяется конкретными условиями задачи и принципиального значения не имеет. Уравнение состояния относительно изменения свободной энергии Fi записывается в виде зависимости:
d Ft = - Si d Tt - pi d Vi + µi d Mi, (1)
где Si — удельная энтропия фазы; p, — давление, действующее со стороны фазы; Hi— химический потенциал фазы, Tt, Vi, М, — принятые независимые переменные (температура, объем и масса i- й фазы или компонента) Уравнение (1) является одной из форм записи основного термодинамического уравнения Гиббса для открытой системы при принятых независимых переменных.
Джозия Уиллард Гиббс Джозия Уиллард Гиббс (1839-1903) — американский физик-теоретик, один из создателей термодинамики и статистической механики. Разработал теорию термодинамических потенциалов, открыл общее условие равновесия гетерогенных систем — правило фаз, вывел уравнения Гиббса — Гельмгольца, Гиббса — Дюгема, адсорбционное уравнение Гиббса. Установил фундаментальный закон статистической физики — распределение Гиббса. Уиллард предложил графическое изображение состояния трехкомпонентной системы (треугольник Гиббса). Заложил основы термодинамики поверхностных явлений и электрохимических процессов. Ввел понятие адсорбции.
При расчете тепломассообменных аппаратов необходимо определять перенос тепла и влаги от одного рабочего тела к другому, т. е. рассматривать процессы, связанные с неравновесным состоянием открытых гетерогенных систем. Основное предположение, из которого исходят в термодинамике необратимых процессов, состоит в том, что соотношение (1), характеризующее равновесное состояние — статику, может быть распространено и на описание неравновесных состояний, т. е. на состояния рабочих тел в динамическом режиме. Такое предположение справедливо при небольших (в термодинамическом смысле) отклонениях систем от равновесного состояния, что характерно для процессов тепломассообмена в аппаратах кондиционирования воздуха, поэтому при их расчете можно пользоваться теоретическими построениями термодинамики необратимых процессов. Следуя выводу полного термодинамического потенциала влажности, уравнение состояния для рабочего вещества можно записать в виде: d F = — S d T +
где S — удельная энтропия всей гетерогенной системы (рабочего вещества): Т — температура системы;
dM — приращение массы компонента (например, влаги в воздухе или растворителя в растворе и т. д) Уравнение (2) удобно для определения состояния рабочих веществ в аппаратах тепло- и массообмена тем, что в нем выделены в самостоятельные слагаемые факторы, определяющие массообмен (второе слагаемое) и теплообмен (первое слагаемое). Рассмотренное термодинамическое построение является теоретической основой, качественно определяющей состояние рабочих веществ в аппаратах тепломассообмена. Обмен теплом и массой между рабочими веществами в аппаратах будет происходить в направлении выравнивания термодинамических потенциалов веществ за счет изменения емкостных показателей. Такие процессы являются переходными. Если разности потенциалов рабочих сред поддерживаются на заданном уровне или определенным образом изменяются за счет внешних воздействий, то на границе рабочих сред происходит обмен энергией и массой, а сами среды изменяют термодинамические потенциалы и емкостные показатели, т. е. в общем случае происходит сложный процесс нестационарного тепло- и массообмена.
При анализе фазовых равновесий и процессов фазовых переходов рабочих веществ большое значение имеет правило Гиббса, которое устанавливает зависимость между числом независимых переменных (степенями свободы системы), определяющих состояние термодинамической системы п, числом компонентов п1 и числом фаз системы n2.
П = п1 — пг + 2. (З)
Для компонента в однофазовом состоянии n = 1 — 1+2=2. Это означает, что система (один компонент в виде одной фазы) будет определена, если заданы две функции состояния, например давление р и температура Т. Для двух фаз одного компонента n = 1, т. е. система обладает только одной степенью свободы. В данном случае одна независимая переменная определяет состояние системы, например, р или Т. Рассматривая однокомпонентную систему, состоящую из трех фаз, из формулы (3) видно, что число степеней свободы такой системы равно нулю. Следовательно, в однокомпонентной системе три фазы могут находиться в равновесии лишь при вполне определенных температуре, давлении и др. В термодинамике атмосферный воздух рассматривают как смесь, состоящую из сухого воздуха и водяного пара, который может быть в перегретом, насыщенном или в сконденсированном взвешенном состоянии в виде капельного или ледяного (при отрицательной температуре) тумана. Последнее состояние является неустойчивым и изучается обычно при решении некоторых специальных задач, например, в холодильной технике. При расчетах систем вентиляции и кондиционирования атмосферный воздух считают бинарной гомогенной смесью, в состав которой входят сухой воздух и водяной пар. Смесь сухого воздуха с перегретым водяным паром называется ненасыщенным влажным воздухом, а смесь сухого воздуха с насыщенным водяным паром - насыщенным влажным воздухом. При этом условие насыщения рассматривается как равновесное состояние между водяным паром во влажном воздухе и водой в жидкой или твердой фазах при одинаковой температуре на плоской поверхности раздела. Количество водяного пара во влажном воздухе изменяется от нуля (сухой воздух) до некоторого максимального значения, которое зависит от температуры и барометрического давления, и в процессах кондиционирования обычно не превышает 3... 4%. Поэтому с достаточной для технических расчетов точностью влажный воздух можно считать идеальным газом, который подчиняется всем законам смеси идеальных газов, хотя в ряде случаев необходимо учитывать реальные свойства водяного пара. Термодинамические свойства сухого воздуха и водяного пара различны, поэтому свойства влажного воздуха зависят от его количественного состава. В технике вентиляции и кондиционирования свойства влажного воздуха характеризуются следующими основными параметрами: температура по сухому термометру t, влагосодержание d, относительная влажность j, плотность r, температура по мокрому термометру tм, температура точки росы tр, барометрическое давление Рб, удельная теплоемкость с и удельная энтальпия J. Согласно закону Дальтона, барометрическое давление влажного воздуха равно сумме парциальных давлений сухого воздуха и водяного пара
Р б = Р с + Р п. (4)
Величины Р б, Р с и Р п измеряют в Па или кПа.
Температура и барометрическое давление атмосферного воздуха зависят от высоты над уровнем моря, географического расположения и погодных условий. На уровне моря в качестве стандартных приняты [3]: температура 15 °С и барометрическое давление 101,325 кПа. Парциальные давления сухого воздуха и водяного пара, входящих в состав влажного воздуха, можно определить в Па по уравнению Клапейрона:
где М с - масса сухой части влажного воздуха; М п - масса водяного пара во влажном воздухе; V - общий объем смеси; Т - абсолютная температура смеси, К. При тепловлажностной обработке и изменении свойств влажного воздуха количество его сухой части остается неизменным, поэтому при рассмотрении тепловлажностного состояния воздуха принято его показатели относить к 1 кг сухой части. Масса водяного пара во влажном воздухе, приходящаяся на 1 кг массы сухой его части, называется влагосодержанием влажного воздуха
Для (1 + d) кг влажного воздуха, т.е. для смеси, содержащей 1 кг сухого воздуха и d кг водяного пара, уравнения состояния имеют вид:
Как видно, парциальное давление водяного пара в ненасыщенном влажном воздухе при определенном барометрическом давлении однозначно определяется влагосодержанием и не зависит от температуры. Относительной влажностью воздуха называется отношение парциального давления водяного пара, содержащегося во влажном воздухе заданного состояния, к парциальному давлению насыщенного водяного пара при той же температуре:
Удельная энтальпия влажного воздуха J - это количество теплоты, содержащееся во влажном воздухе при заданных температуре и давлении, отнесенное к 1 кг сухого воздуха. Энтальпия смеси газов равна сумме энтальпий компонентов, входящих в смесь. Следовательно, удельная энтальпия влажного воздуха представляет сумму энтальпий сухого воздуха и водяного пара.
J = J c + J п - d, (10)
где J c - удельная энтальпия сухого воздуха, кДж/кг с.в.; J п - удельная энтальпия водяного пара, кДж/кг п. В ненасыщенном влажном воздухе водяной пар находится в перегретом состоянии, т.е. его температура выше температуры насыщения. Если влажный воздух охлаждать без изменения давления, то количество содержащегося в нем водяного пара будет оставаться неизменным, следовательно, процесс охлаждения будет идти при постоянном влагосодержании и парциальном давлении пара. Такой процесс может протекать до тех пор, пока температура воздуха и пара не понизится до температуры насыщения, т.к. при дальнейшем охлаждении воздуха из него начнет выпадать влага в виде капель или инея.
Температура, соответствующая состоянию насыщения влажного воздуха при заданном значении влагосодержания или парциального давления, называется температурой точки росы. Температура точки росы является предельной температурой, до которой можно охлаждать влажный воздух при постоянном влагосодержании без выпадения конденсата.
Простая гомогенная система в равновесном состоянии характеризуется определенными значениями параметров состояния v, P и Т. Уравнение, устанавливающее связь между давлением, температурой и удельным объемом системы, называется термическим уравнением состояния и имеет вид:
F (R, v, T) = 0. (11)
Состояние системы вполне определяется заданием двух из указанных параметров, т.к. любой из трех параметров является для каждого равновесного состояния однозначной функцией двух заданных. Поэтому можно записать, что
P = f 1(v, T); v = f 2(R, T); T = f 3(v, P). (12)
Термическое уравнение состояния газов при малых давлениях принимает простое выражение. Если по измеренным значения R, v и Т рассчитать величину P × v / T, то получим:
Константа R г называется газовой постоянной и имеет для каждого газа свое значение. Она представляет собой работу 1 кг газа при постоянном давлении и при изменении температуры на 1 градус. Используя понятие газовой постоянной, уравнение состояния можно записать в виде:
Pv = R г T. (14)
Газ, состояние которого точно описывается уравнением (14), называется идеальным, а само уравнение - термическим уравнением состояния идеальных газов, или уравнением Клапейрона. Для m кг идеального газа уравнение состояния имеет вид:
PV = mR г T, (15)
где V - объем газа, м3. Умножая обе части уравнения (15) на молекулярную массу m, получим
PV m = m R г T, (16)
где V m = v ×m - объем, занимаемый одним молем газа.
Связь между температурой и давлением на линии фазовых переходов устанавливает уравнение Клапейрона—Клаузиуса.
Бенуа Поль Эмиль КЛАПЕЙРОН Benoît Paul Émile Clapeyron, 1799–1864 Бенуа Поль Эмиль Клапейрон – французский физик и инженер, член Парижской АН (с 1858). Родился в Париже. В 1818 г. окончил Политехническую школу. В 1820-1830 гг. работал в Петербурге в Институте инженеров путей сообщения. После возвращения во Францию был профессором (с 1844) Школы мостов и дорог в Париже. Осуществлял надзор над строительством первой французской железнодорожной линии от Парижа до Версаля и Сен-Жермена. Физические исследования Клапейрона посвящены теплоте, пластичности и равновесию твердых тел. Он придал в 1834 г. математическую форму идеям C. Карно, первым оценив большое научное значение его труда «Размышления о движущей силе огня», содержащего фактически формулировку второго начала термодинамики. Исходя из этих идей, впервые ввёл в термодинамику графический метод – индикаторные диаграммы, в частности предложил систему координат р-V.
В 1834 г. вывел уравнение состояния идеального газа, объединяющее закон Бойля – Мариотта, закон Гей-Люссака и закон Авогадро, обобщённое в 1874 г. Д.И. Менделеевым (уравнение Менделеева – Клапейрона). Вывел уравнение, устанавливающее связь между температурой плавления и кипения вещества и давлением, которое было термодинамически обосновано в 1851 г. Р. Клаузиусом (уравнение Клапейрона – Клаузиуса).
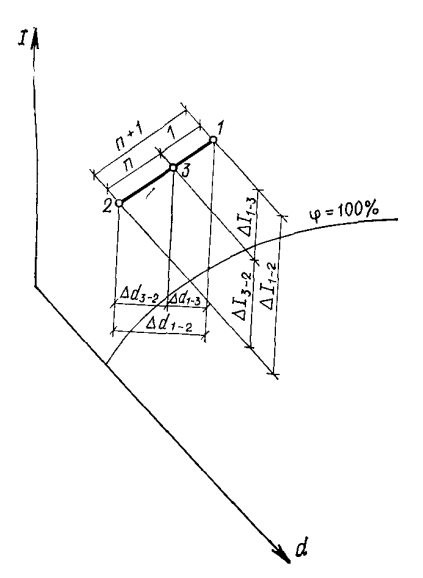
Процессы смешения При кондиционировании в ряде случаев наружный воздух, подаваемый в помещение, смешивают с внутренним воздухом (рециркуляция внутреннего воздуха). Возможны и другие случаи, связанные с перемешиванием масс воздуха разного состояния. Процесс смешения воздуха при построении на I — d-диаграмме изображается прямой, соединяющей точки состояния воздуха смешиваемых масс. Точка смеси всегда располагается на этой прямой и делит ее на отрезки, обратно пропорциональные смешиваемым количествам воздуха. Если смешать воздух состояния 1 (рис. 4) в количестве G с воздухом состояния 2 в количестве nG, то точка смеси 3 разделит отрезок 1—2 или его проекции
Таким образом, чтобы найти точку смеси, нужно прямую 1 —2 или ее проекции разделить на n+1 частей и отложить от точки 1 одну часть, оставив п частей до точки 2. Такое построение определит положение точки смеси. Возможен случай, когда точка смеси 3' окажется в области ниже линии ф= 100%. Это значит, что при смешивании будет образовываться туман (конденсация, образование капель из водяного пара, содержащегося в воздухе). Если принять температуру выпадающей влаги, близкой к температуре мокрого термометра, соответствующей (Iз- = const) точке смеси 3' (рис. 5), то действительные параметры точки смеси 3 будут соответствовать пересечению линий Iз' = const и Ф= 100%.
Рис. 4
Рис. 5
Термодинамика состояния рабочих сред тепло- и массообменных аппаратов кондиционирования. Расчет УКВ заключается в определении параметров состояния обменивающихся рабочих сред и потоков тепла и массы между ними. Рабочие среды в обменных аппаратах представляют собой гомогенные либо гетерогенные системы. Гомогенной называют такую систему, химический состав и физические свойства которой во всех частях одинаковы и изменяются непрерывно без скачка от одной точки системы к другой. Гетерогенной называется система, состоящая из двух и более различных гомогенных областей. Гомогенные области в гетерогенной системе являются компонентами или фазами различных компонентов системы. После разделения гетерогенной системы на компоненты и фазы ее можно полностью термодинамически описать. В термодинамике принят ряд характеристических функций, определяющих состояние отдельных компонентов и фаз. С помощью этих функций могут быть в явной форме выражены все термодинамические свойства состояния компонентов. Выбор тех или иных функций для расчетов определяется конкретными условиями задачи и принципиального значения не имеет. Уравнение состояния относительно изменения свободной энергии Fi записывается в виде зависимости:
d Ft = - Si d Tt - pi d Vi + µi d Mi, (1)
где Si — удельная энтропия фазы; p, — давление, действующее со стороны фазы; Hi— химический потенциал фазы, Tt, Vi, М, — принятые независимые переменные (температура, объем и масса i- й фазы или компонента) Уравнение (1) является одной из форм записи основного термодинамического уравнения Гиббса для открытой системы при принятых независимых переменных.
Джозия Уиллард Гиббс Джозия Уиллард Гиббс (1839-1903) — американский физик-теоретик, один из создателей термодинамики и статистической механики. Разработал теорию термодинамических потенциалов, открыл общее условие равновесия гетерогенных систем — правило фаз, вывел уравнения Гиббса — Гельмгольца, Гиббса — Дюгема, адсорбционное уравнение Гиббса. Установил фундаментальный закон статистической физики — распределение Гиббса. Уиллард предложил графическое изображение состояния трехкомпонентной системы (треугольник Гиббса). Заложил основы термодинамики поверхностных явлений и электрохимических процессов. Ввел понятие адсорбции.
При расчете тепломассообменных аппаратов необходимо определять перенос тепла и влаги от одного рабочего тела к другому, т. е. рассматривать процессы, связанные с неравновесным состоянием открытых гетерогенных систем. Основное предположение, из которого исходят в термодинамике необратимых процессов, состоит в том, что соотношение (1), характеризующее равновесное состояние — статику, может быть распространено и на описание неравновесных состояний, т. е. на состояния рабочих тел в динамическом режиме. Такое предположение справедливо при небольших (в термодинамическом смысле) отклонениях систем от равновесного состояния, что характерно для процессов тепломассообмена в аппаратах кондиционирования воздуха, поэтому при их расчете можно пользоваться теоретическими построениями термодинамики необратимых процессов. Следуя выводу полного термодинамического потенциала влажности, уравнение состояния для рабочего вещества можно записать в виде: d F = — S d T +
где S — удельная энтропия всей гетерогенной системы (рабочего вещества): Т — температура системы;
dM — приращение массы компонента (например, влаги в воздухе или растворителя в растворе и т. д) Уравнение (2) удобно для определения состояния рабочих веществ в аппаратах тепло- и массообмена тем, что в нем выделены в самостоятельные слагаемые факторы, определяющие массообмен (второе слагаемое) и теплообмен (первое слагаемое). Рассмотренное термодинамическое построение является теоретической основой, качественно определяющей состояние рабочих веществ в аппаратах тепломассообмена. Обмен теплом и массой между рабочими веществами в аппаратах будет происходить в направлении выравнивания термодинамических потенциалов веществ за счет изменения емкостных показателей. Такие процессы являются переходными. Если разности потенциалов рабочих сред поддерживаются на заданном уровне или определенным образом изменяются за счет внешних воздействий, то на границе рабочих сред происходит обмен энергией и массой, а сами среды изменяют термодинамические потенциалы и емкостные показатели, т. е. в общем случае происходит сложный процесс нестационарного тепло- и массообмена. При анализе фазовых равновесий и процессов фазовых переходов рабочих веществ большое значение имеет правило Гиббса, которое устанавливает зависимость между числом независимых переменных (степенями свободы системы), определяющих состояние термодинамической системы п, числом компонентов п1 и числом фаз системы n2.
П = п1 — пг + 2. (З)
Для компонента в однофазовом состоянии n = 1 — 1+2=2. Это означает, что система (один компонент в виде одной фазы) будет определена, если заданы две функции состояния, например давление р и температура Т. Для двух фаз одного компонента n = 1, т. е. система обладает только одной степенью свободы. В данном случае одна независимая переменная определяет состояние системы, например, р или Т. Рассматривая однокомпонентную систему, состоящую из трех фаз, из формулы (3) видно, что число степеней свободы такой системы равно нулю. Следовательно, в однокомпонентной системе три фазы могут находиться в равновесии лишь при вполне определенных температуре, давлении и др. В термодинамике атмосферный воздух рассматривают как смесь, состоящую из сухого воздуха и водяного пара, который может быть в перегретом, насыщенном или в сконденсированном взвешенном состоянии в виде капельного или ледяного (при отрицательной температуре) тумана. Последнее состояние является неустойчивым и изучается обычно при решении некоторых специальных задач, например, в холодильной технике. При расчетах систем вентиляции и кондиционирования атмосферный воздух считают бинарной гомогенной смесью, в состав которой входят сухой воздух и водяной пар. Смесь сухого воздуха с перегретым водяным паром называется ненасыщенным влажным воздухом, а смесь сухого воздуха с насыщенным водяным паром - насыщенным влажным воздухом. При этом условие насыщения рассматривается как равновесное состояние между водяным паром во влажном воздухе и водой в жидкой или твердой фазах при одинаковой температуре на плоской поверхности раздела. Количество водяного пара во влажном воздухе изменяется от нуля (сухой воздух) до некоторого максимального значения, которое зависит от температуры и барометрического давления, и в процессах кондиционирования обычно не превышает 3... 4%. Поэтому с достаточной для технических расчетов точностью влажный воздух можно считать идеальным газом, который подчиняется всем законам смеси идеальных газов, хотя в ряде случаев необходимо учитывать реальные свойства водяного пара. Термодинамические свойства сухого воздуха и водяного пара различны, поэтому свойства влажного воздуха зависят от его количественного состава. В технике вентиляции и кондиционирования свойства влажного воздуха характеризуются следующими основными параметрами: температура по сухому термометру t, влагосодержание d, относительная влажность j, плотность r, температура по мокрому термометру tм, температура точки росы tр, барометрическое давление Рб, удельная теплоемкость с и удельная энтальпия J. Согласно закону Дальтона, барометрическое давление влажного воздуха равно сумме парциальных давлений сухого воздуха и водяного пара
Р б = Р с + Р п. (4)
Величины Р б, Р с и Р п измеряют в Па или кПа. Температура и барометрическое давление атмосферного воздуха зависят от высоты над уровнем моря, географического расположения и погодных условий. На уровне моря в качестве стандартных приняты [3]: температура 15 °С и барометрическое давление 101,325 кПа. Парциальные давления сухого воздуха и водяного пара, входящих в состав влажного воздуха, можно определить в Па по уравнению Клапейрона:
где М с - масса сухой части влажного воздуха; М п - масса водяного пара во влажном воздухе; V - общий объем смеси; Т - абсолютная температура смеси, К. При тепловлажностной обработке и изменении свойств влажного воздуха количество его сухой части остается неизменным, поэтому при рассмотрении тепловлажностного состояния воздуха принято его показатели относить к 1 кг сухой части. Масса водяного пара во влажном воздухе, приходящаяся на 1 кг массы сухой его части, называется влагосодержанием влажного воздуха
Для (1 + d) кг влажного воздуха, т.е. для смеси, содержащей 1 кг сухого воздуха и d кг водяного пара, уравнения состояния имеют вид:
Как видно, парциальное давление водяного пара в ненасыщенном влажном воздухе при определенном барометрическом давлении однозначно определяется влагосодержанием и не зависит от температуры. Относительной влажностью воздуха называется отношение парциального давления водяного пара, содержащегося во влажном воздухе заданного состояния, к парциальному давлению насыщенного водяного пара при той же температуре:
Удельная энтальпия влажного воздуха J - это количество теплоты, содержащееся во влажном воздухе при заданных температуре и давлении, отнесенное к 1 кг сухого воздуха. Энтальпия смеси газов равна сумме энтальпий компонентов, входящих в смесь. Следовательно, удельная энтальпия влажного воздуха представляет сумму энтальпий сухого воздуха и водяного пара.
J = J c + J п - d, (10)
где J c - удельная энтальпия сухого воздуха, кДж/кг с.в.; J п - удельная энтальпия водяного пара, кДж/кг п. В ненасыщенном влажном воздухе водяной пар находится в перегретом состоянии, т.е. его температура выше температуры насыщения. Если влажный воздух охлаждать без изменения давления, то количество содержащегося в нем водяного пара будет оставаться неизменным, следовательно, процесс охлаждения будет идти при постоянном влагосодержании и парциальном давлении пара. Такой процесс может протекать до тех пор, пока температура воздуха и пара не понизится до температуры насыщения, т.к. при дальнейшем охлаждении воздуха из него начнет выпадать влага в виде капель или инея. Температура, соответствующая состоянию насыщения влажного воздуха при заданном значении влагосодержания или парциального давления, называется температурой точки росы. Температура точки росы является предельной температурой, до которой можно охлаждать влажный воздух при постоянном влагосодержании без выпадения конденсата.
Простая гомогенная система в равновесном состоянии характеризуется определенными значениями параметров состояния v, P и Т. Уравнение, устанавливающее связь между давлением, температурой и удельным объемом системы, называется термическим уравнением состояния и имеет вид:
F (R, v, T) = 0. (11)
Состояние системы вполне определяется заданием двух из указанных параметров, т.к. любой из трех параметров является для каждого равновесного состояния однозначной функцией двух заданных. Поэтому можно записать, что
P = f 1(v, T); v = f 2(R, T); T = f 3(v, P). (12)
Термическое уравнение состояния газов при малых давлениях принимает простое выражение. Если по измеренным значения R, v и Т рассчитать величину P × v / T, то получим:
Константа R г называется газовой постоянной и имеет для каждого газа свое значение. Она представляет собой работу 1 кг газа при постоянном давлении и при изменении температуры на 1 градус. Используя понятие газовой постоянной, уравнение состояния можно записать в виде:
Pv = R г T. (14)
Газ, состояние которого точно описывается уравнением (14), называется идеальным, а само уравнение - термическим уравнением состояния идеальных газов, или уравнением Клапейрона. Для m кг идеального газа уравнение состояния имеет вид:
PV = mR г T, (15)
где V - объем газа, м3. Умножая обе части уравнения (15) на молекулярную массу m, получим
PV m = m R г T, (16)
где V m = v ×m - объем, занимаемый одним молем газа.
Связь между температурой и давлением на линии фазовых переходов устанавливает уравнение Клапейрона—Клаузиуса.
Бенуа Поль Эмиль КЛАПЕЙРОН Benoît Paul Émile Clapeyron, 1799–1864 Бенуа Поль Эмиль Клапейрон – французский физик и инженер, член Парижской АН (с 1858). Родился в Париже. В 1818 г. окончил Политехническую школу. В 1820-1830 гг. работал в Петербурге в Институте инженеров путей сообщения. После возвращения во Францию был профессором (с 1844) Школы мостов и дорог в Париже. Осуществлял надзор над строительством первой французской железнодорожной линии от Парижа до Версаля и Сен-Жермена. Физические исследования Клапейрона посвящены теплоте, пластичности и равновесию твердых тел. Он придал в 1834 г. математическую форму идеям C. Карно, первым оценив большое научное значение его труда «Размышления о движущей силе огня», содержащего фактически формулировку второго начала термодинамики. Исходя из этих идей, впервые ввёл в термодинамику графический метод – индикаторные диаграммы, в частности предложил систему координат р-V.
В 1834 г. вывел уравнение состояния идеального газа, объединяющее закон Бойля – Мариотта, закон Гей-Люссака и закон Авогадро, обобщённое в 1874 г. Д.И. Менделеевым (уравнение Менделеева – Клапейрона). Вывел уравнение, устанавливающее связь между температурой плавления и кипения вещества и давлением, которое было термодинамически обосновано в 1851 г. Р. Клаузиусом (уравнение Клапейрона – Клаузиуса).
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.72 (0.015 с.) |

 d М, (2)
d М, (2) ; (5)
; (5)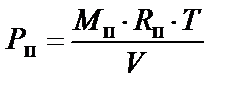 , (6)
, (6)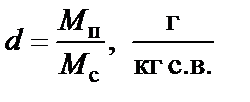 . (7)
. (7) . (8)
. (8) . (9)
. (9) . (13)
. (13) на части 1—3, 3—2 или
на части 1—3, 3—2 или 
 (26)
(26)