Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Rudolf Julius Emanuel Clausius, 1822–88Содержание книги Поиск на нашем сайте
Немецкий физик, один из основателей термодинамики и молекулярно-кинетической теории теплоты. Учился в Берлинском университете (с 1840). В 1850—57 преподавал в Берлине и Цюрихе. Профессор университетов в Цюрихе (с 1857), Вюрцбурге (с 1867), Бонне (с 1869). Клаузиус первым понял и проанализировал глубокие идеи С. Карно и оценил их значение для теории теплоты и тепловых машин. Развивая эти идеи, Клаузиус в 1850 (одновременно с У. Томсоном)дал первую формулировку второго начала термодинамики; "Теплота не может сама собою перейти от более холодного тела к более тёплому". Клаузиус доказал, что не существует способа передачи теплоты от более холодного тела к более нагретому без того, чтобы в природе не произошло каких-либо изменений, которые могли бы компенсировать такой переход. В 1865 Клаузиус ввёл понятие энтропии. Ошибочно распространив принцип возрастания энтропии замкнутой системы на всю Вселенную, К. высказал мысль о тепловой смерти Вселенной.
Уравнение Клапейрона — Клаузиуса, термодинамическое уравнение, относящееся к процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.). Согласно уравнению Клапейрона — Клаузиуса, теплота фазового перехода (например, теплота испарения, теплота плавления) при равновесно протекающем процессе определяется выражением:
где Т — температура перехода (процесс изотермический), dp/dT — значение производной от давления по температуре при данной температуре перехода, (V2—V1) — изменение объёма вещества при переходе его из первой фазы во вторую. Первоначально уравнение было получено в 1834 Б. П. Э. Клапейроном из анализа Карно цикла для конденсирующегося пара, находящегося в тепловом равновесии с жидкостью. В 1850 P. Клаузиус усовершенствовал уравнение и распространил его на другие фазовые переходы. Уравнение Клапейрона — Клаузиуса применимо к любым фазовым переходам, сопровождающимся поглощением или выделением теплоты (так называемым фазовым переходом 1 рода), и является прямым следствием условий фазового равновесия, из которых оно и выводится. Уравнение Клапейрона — Клаузиуса может служить для расчёта любой из величин, входящих в уравнение, если остальные известны. В частности, с его помощью рассчитывают теплоты испарения, экспериментальное определение которых сопряжено со значительными трудностями. Часто уравнение Клапейрона — Клаузиуса записывают относительно производных dp/dT или dT/dp:
Для процессов испарения и сублимации dp/dT выражает изменение давления насыщенного пара р с температурой Т, а для процессов плавления и полиморфного превращения dT/dp определяет изменение температуры перехода с давлением. Иными словами, уравнение Клапейрона — Клаузиуса является дифференциальным уравнением кривой фазового равновесия в переменных р, Т. Для решения уравнения Клапейрона — Клаузиуса необходимо знать, как изменяются с температурой и давлением величины L, V1 и V2, что представляет сложную задачу. Обычно эту зависимость устанавливают эмпирически и решают уравнение Клапейрона — Клаузиуса численно. Уравнение Клапейрона — Клаузиуса применимо как к чистым веществам, так и к растворам и отдельным компонентам растворов. В последнем случае уравнение Клапейрона — Клаузиуса связывает парциальное давление насыщенного пара данного компонента с его парциальной теплотой испарения. Особый интерес представляют условия фазового перехода при испарении воды в воздух. В этом случае давление над поверхность жидкости рж равно сумме давлений пара и воздуха, и условия фазового равновесия имеют вид Т=Тж—Тп и рж = Рп+Рв Из уравнения Клапейрона—Клаузиуса имеем:
Так как
В частности для водяного пара, если в качестве реперной точки принять T0 = ТПо = 0°С = 273 К, при которой r = 2500 кДж/кг, R = 0,462 кДж/(кг-К), рПо = 610,8 Па, то связь между давлением и температурой па линии насыщения «пар—вода» будет выражаться приближенной для реальных условий зависимостью:
рп = 610,8 ехр [5413,42 (1/273 — 1 /Г)]. (21)
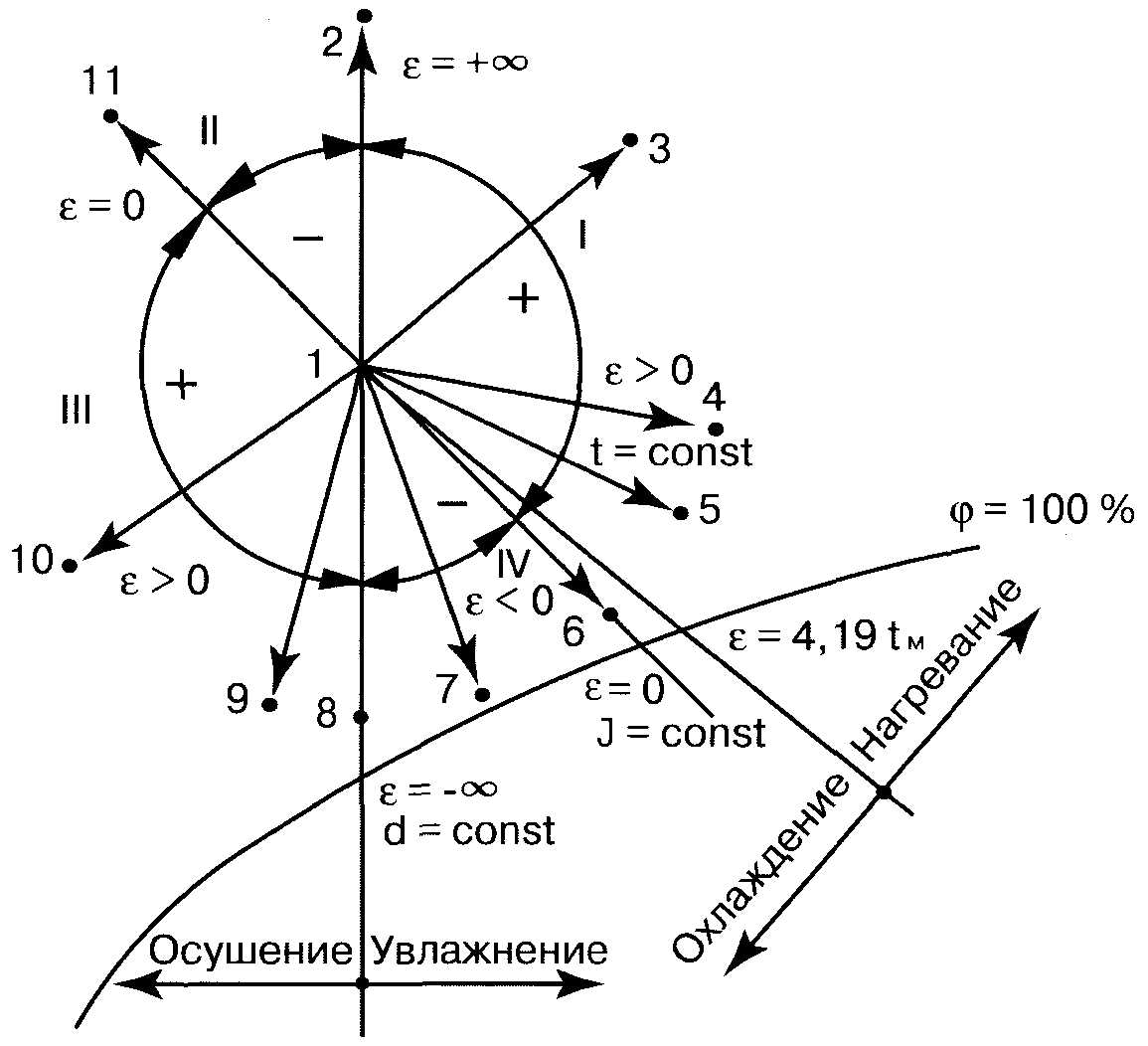
Термодинамика влажного воздуха, все характеристики его состояния. При кондиционировании воздуха происходят изменения его тепловдажностного состояния, которые удобно прослеживать и рассчитывать с помощью I —d-диаграммы. Нанесем на 1-d- диаграмму точку 1, соответствующую начальному состоянию воздуха, и точку 2, соответствующую его измененному состоянию (рис.1). Линия, соединяющая эти две точки, характеризует изменение тепловлажностного состояния воздуха и называется лучом процесса. Положение луча процесса в I —d-диаграмме определяют угловым коэффициентом
Коэффициент Выражение (14) можно преобразовать умножив числитель и знаменатель на расход воздуха G, кг/ч, участвующего в процессе:
где Qn — поток полной теплоты, обмененной в процессе изменения состояния воздуха, кДж/ч; Wизб — расход влаги, обмененной в процессе изменения состояния воздуха, кг/ч. На рис. 1 показаны лучи характерных изменений состояния влажного воздуха и соответствующие им значения углового коэффициента.
Рис.1. Угловой коэффициент на J - d диаграмме
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.219.203 (0.009 с.) |

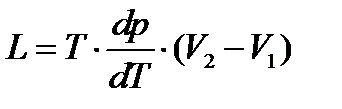 , (17)
, (17)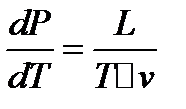 (18)
(18)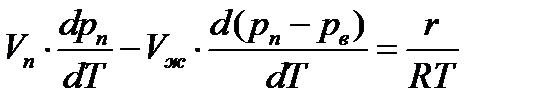 (19)
(19)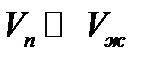 ,a dpп /dT и d(pп+pB)/dT величины одного порядка, тo приходим к зависимости:
,a dpп /dT и d(pп+pB)/dT величины одного порядка, тo приходим к зависимости: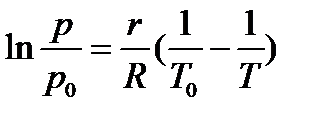 (20)
(20)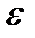 . Если влажный воздух изменил свое состояние от начальных значений I1 и d1 до конечных значений I2 и d2, то можно записать отношение:
. Если влажный воздух изменил свое состояние от начальных значений I1 и d1 до конечных значений I2 и d2, то можно записать отношение: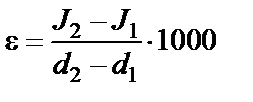 (22)
(22)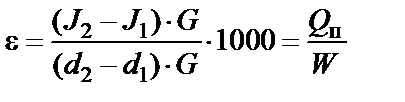 (23)
(23)