
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 2. Первое начало термодинамики.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Первое начало термодинамики получено на основании множества опытных данных – по сути это закон сохранения энергии с учетом тепловых явлений. Оно имеет несколько формулировок.
Первое начало термодинамики «разрешает» построение такой тепловой машины, которая переводила бы всю затраченную теплоту в работу. Такая машина получила название вечного двигателя второго рода. Но согласно второму началу термодинамики создание такой машины невозможно. Иначе говоря, в любой тепловой машине всегда получается работы меньше, чем затрачивается энергии, часть затраченной энергии рассеивается в окружающей среде. Вопрос 3.Изохорический процесс. Его можно осуществить, нагревая газ при закрепленном поршне. Подставим выражения для dQ и dU.
Вопрос 5.Изобарический процесс. Нагреваем газ при свободном ходе поршня – поршень будет перемещаться, когда давление внутри превышает давление извне (а оно постоянно). Если эти давления сравняются, поршень остановится.
Вопрос 4.Изотермический процесс. Представим себе, что цилиндр с поршнем помещен в очень большой сосуд с жидкостью. Вначале температура Т у жидкости и газа одинакова. Будем очень медленно поднимать поршень. Газ расширится, его температура уменьшится на dT, и теплота от жидкости перейдет к газу. При этом температура жидкости практически не изменится, т.к. у нее очень большой запас внутренней энергии. Перемещая бесконечно медленно поршень, мы в результате нагреем газ при постоянной температуре. Опуская поршень, мы таким же образом можем охладить газ. Естественно, такой процесс реально не осуществим, это идеализация, но она важна при теоретическом рассмотрении процессов в газах.
Вопрос 6. Адиабатический процесс – это процесс, происходящий без теплообмена с окружающей средой. Его можно практически осуществить двумя способами: 1)теплоизолировать цилиндр – лучший теплоизолятор – вакуум, и перемещать поршень или 2) очень быстро переместить поршень, так чтобы теплообмен с окружающей средой не успел осуществиться (теплообмен – медленный процесс при не очень больших DТ).
Таким образом, на основе I начала термодинамики мы получили уравнение адиабатического процесса. Так как при таком процессе изменяются все три параметра p,V,T, то можно записать три уравнения процесса:
Вопрос 7.Работа. Работу, совершаемую при адиабатическом процессе можно найти, проинтегрировав уравнение I начала термодинамики:
Пусть газ находится в некотором состоянии с объемом V. Зададимся вопросом, как выгоднее проводить (быстро поднять поршень в цилиндре), расширение газа – адиабатически или изотермически? Ответ – адиабатически т.к. площадь под адиабатой меньше. А сжимать газ выгоднее изотермически (очень медленно). Вопрос 8.Теплоемкость газов.
Тема 16. Вопрос 1. Энтропия II начало термодинамики, как и I начало, является обобщением большого числа опытных фактов и имеет несколько формулировок. Введем сначала понятие «энтропия», которое играет ключевую роль в термодинамике. Э нтропия - S – одна из важнейших термодинамических функций, характеризующая состояние или возможные изменения состояния вещества – это многогранное понятие.
Энтропия определяется следующим образом.
Для обратимых процессов в идеальных газах можно получить формулы для вычисления энтропии в различных процессах. Выразим dQ из I начала и подставим в выражение для dS.
общее выражение для изменения энтропии в обратимых процессах.
Интегрируя, получим выражения для изменения энтропии в различных изопроцессах в идеальных газах. Вопрос 2,3,4.изобарический, изохорический, изотермический
Во всех расчетах энтропии имеет значение только разность энтропий конечного и начального состояний системы
2) Энтропия мера рассеяния энергии.
3) Энтропия – мера беспорядка системы Введем понятие термодинамической вероятности.Пусть мы имеет ящик, разделенный на n отсеков. В ящике по всем отсекам свободно перемещается N молекул. В первом отсеке окажется N1 молекул, во втором отсеке N2 молекул,…, в n -ом отсеке - Nn молекул. Число способов w, которыми можно распределить N молекул по n состояниям (отсекам) называется термодинамической вероятностью. Иначе говоря, термодинамическая вероятность показывает, сколькими микро распределениями можно получить данное макро распределение Она вычисляется по формуле: [1]
Для примера вычисления w рассмотрим систему, состоящую из трех молекул 1, 2 и 3, которые свободно перемещаются в ящике с тремя отсеками. [2] В данном примере N = 3 (три молекулы) и n = 3 (три отсека), молекулы считаются различимыми. В первом случае макрораспределение – это равномерное распределение молекул по отсекам, оно может осуществиться 6-ью микрораспределениями. Вероятность такого распределение самая большая. Равномерное распределение можно назвать «беспорядком» (по аналогии с разбросанными вещами в комнате) В последнем случае, когда молекулы собираются только в одном отсеке вероятность наименьшая. Проще говоря, из повседневных наблюдений мы знаем, что молекулы воздуха более или менее равномерно распределяются в помещении, и практически совершенно невероятно, чтобы все молекулы собрались в одном углу комнаты. Однако теоретически такая вероятность существует. Больцман постулировал, что энтропия прямо пропорциональна натуральному логарифму термодинамической вероятности:
Следовательно, энтропию можно назвать мерой беспорядка системы.
Вопрос 6.Теперь мы можем сформулировать II начало термодинамики.
Вопрос 7. КРУГОВЫЕ ПРОЦЕССЫ (ЦИКЛЫ) Круговым процессом или циклом называется такой процесс, при котором система, пройдя ряд состояний, возвращается в исходное состояние. Если процесс осуществляется по часовой стрелке, он называется прямым, против часовой стрелки – обратным. Т.к. внутренняя энергия является функцией состояния, то в круговом процессе
Рассмотрим цикл Карно для идеальной тепловой машины. Предполагается, что рабочее тело – идеальный газ, трение отсутствует. Этот цикл, состоящий из двух изотерм и двух адиабат, реально не осуществим, но он сыграл огромную роль в развитии термодинамики и теплотехники и позволил проанализировать коэффициент полезного действия (КПД) тепловых машин.
Таким образом, за цикл газу было сообщено Q1 теплоты, холодильнику передано Q2 теплоты и получена работа А.
Из полученного выражения следует, что: 1) КПД всегда меньше единицы, 2)КПД не зависит от рода рабочего тела, а только от температуры нагревателя и холодильника, 3)чтобы повысить КПД нужно увеличить температуру нагревателя и уменьшить температуру холодильника. В современных двигателях в качестве нагревателя используются горючие смеси - бензин, керосин, дизельное топливо и др., имеющие определенные температуры горения. Холодильником служит чаще всего окружающая среда. Следовательно, реально увеличить КПД можно только за счет уменьшения трения в различных узлах двигателя и машины.
Тема 18.Вопрос 1.АГРЕГАТНЫЕ СОСТОЯНИЯ ВЕЩЕСТВА
Кроме потенциальной, молекула обладает еще и кинетической энергией. Минимальная потенциальная энергия у каждого сорта молекул своя, а кинетическая энергия зависит от температуры вещества (Екин ~ кТ). В зависимости от соотношения между этими энергиями данное вещество может находиться в том или ином агрегатном состоянии. Например, вода может быть в твердом состоянии (лед), в жидком и в виде пара.
У инертных газов Umin невелики, поэтому они переходят в жидкое состояние при очень низких температурах. У металлов большие величины Umin поэтому они находятся в твердом состоянии вплоть до температуры плавления – это могут быть сотни и тысячи градусов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 648; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |



 ;
; 




 теплота идет не только на увеличение внутренней энергии, но и на работу против внешних сил
теплота идет не только на увеличение внутренней энергии, но и на работу против внешних сил

 становится бесконечно большой, т.е. все тепло, подводимое к газу «перерабатывается» им и переводится в работу
становится бесконечно большой, т.е. все тепло, подводимое к газу «перерабатывается» им и переводится в работу
 ²
²
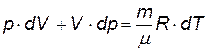

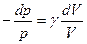




 ,
,  - показатель степени адиабаты.
- показатель степени адиабаты.


 .
.
 или
или 

 Из приведенных выше формул следует, что теплоемкость идеального газа не зависит от температуры газа, а определяется только числом степеней свободы молекул. Для многих одноатомных и двухатомных газов опыт подтверждает этот вывод для умеренных температур. Но при низких и высоких температурах наблюдается характерная зависимость теплоемкости от температуры. На графике приведена несколько идеализированная зависимость молярной теплоемкости от температуры для двухатомного газа. Простейшее объяснение такой зависимости состоит в следующем. При низких температурах преобладает поступательное движение молекул. С ростом температуры все больше молекул начинают участвовать во вращательном движении. С дальнейшим повышением температуры более интенсивно происходят колебания атомов в молекулах. В действительности объяснить зависимость теплоемкости от температуры можно только на основе квантовой механики.
Из приведенных выше формул следует, что теплоемкость идеального газа не зависит от температуры газа, а определяется только числом степеней свободы молекул. Для многих одноатомных и двухатомных газов опыт подтверждает этот вывод для умеренных температур. Но при низких и высоких температурах наблюдается характерная зависимость теплоемкости от температуры. На графике приведена несколько идеализированная зависимость молярной теплоемкости от температуры для двухатомного газа. Простейшее объяснение такой зависимости состоит в следующем. При низких температурах преобладает поступательное движение молекул. С ростом температуры все больше молекул начинают участвовать во вращательном движении. С дальнейшим повышением температуры более интенсивно происходят колебания атомов в молекулах. В действительности объяснить зависимость теплоемкости от температуры можно только на основе квантовой механики. 1) Энтропия – это функция состояния. Введение таких величин ценно тем, что при любых процессах изменение функции состояния одинаково, поэтому сложный реальный процесс можно заменить «выдуманными» простыми процессами. Например, реальный процесс перехода системы из состояния А в состояние В (см. рис.) можно заменить на два процесса: изохорический А®С и изобарический С®В.
1) Энтропия – это функция состояния. Введение таких величин ценно тем, что при любых процессах изменение функции состояния одинаково, поэтому сложный реальный процесс можно заменить «выдуманными» простыми процессами. Например, реальный процесс перехода системы из состояния А в состояние В (см. рис.) можно заменить на два процесса: изохорический А®С и изобарический С®В.


 +
+ 



 называется свободной энергией
величина
называется свободной энергией
величина  называется связанной энергией
называется связанной энергией

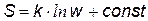

 , но передача теплоты в количестве 10-11 эрг =10-18 Дж дает уже отношение вероятностей @ 2,7.
, но передача теплоты в количестве 10-11 эрг =10-18 Дж дает уже отношение вероятностей @ 2,7.


 Устройство, в котором затрачивается теплота, а получается работа, называется тепловой машиной. Все тепловые машины работают по прямому циклу, состоящему из различных процессов. Устройство, работающее по обратному циклу, называется холодильной машиной. В холодильной машине затрачивается работа, а в результате от холодного тела отнимается теплота, т.е. происходит дополнительное охлаждение этого тела.
Устройство, в котором затрачивается теплота, а получается работа, называется тепловой машиной. Все тепловые машины работают по прямому циклу, состоящему из различных процессов. Устройство, работающее по обратному циклу, называется холодильной машиной. В холодильной машине затрачивается работа, а в результате от холодного тела отнимается теплота, т.е. происходит дополнительное охлаждение этого тела.





 (
( - из уравнений адиабат)
- из уравнений адиабат)

 Т1 – температура нагревателя
Т2 – температура холодильника
Т1 – температура нагревателя
Т2 – температура холодильника
 Молекулы представляют собой сложные системы электрически заряженных частиц. Основная масса молекулы и весь ее положительный заряд сосредоточены в ядрах, их размеры порядка 10-15 - 10-14 м, а размер самой молекулы, включая электронную оболочку, примерно 10-10 м. В целом молекула электрически нейтральна. Электрическое поле ее зарядов в основном сосредоточено внутри молекулы и за ее пределами резко убывает. При взаимодействии двух молекул одновременно проявляются и силы притяжения и силы отталкивания, они по-разному зависят от расстояния между молекулами (см рис.- пунктирные линии). Одновременное действие межмолекулярных сил дает зависимость силы F от расстояния r между молекулами, характерную и для двух молекул, и атомов, и ионов (сплошная кривая). На больших расстояния молекулы практически не взаимодействуют, на очень малых расстояния преобладают силы отталкивания. На расстояниях, равных нескольким диаметрам молекул действуют силы притяжения. Расстояние ro между центрами двух молекул, на котором F=0, - это положение равновесия. Так как сила связана с потенциальной энергией F=-dEпот /dr, то интегрирование даст зависимость потенциальной энергии от r (потенциальная кривая). Равновесное положение соответствует минимуму потенциальной энергии - Umin. Для различных молекул вид потенциальной кривой аналогичен, но числовые значения ro и Umin различны и определяются природой данных молекул.
Молекулы представляют собой сложные системы электрически заряженных частиц. Основная масса молекулы и весь ее положительный заряд сосредоточены в ядрах, их размеры порядка 10-15 - 10-14 м, а размер самой молекулы, включая электронную оболочку, примерно 10-10 м. В целом молекула электрически нейтральна. Электрическое поле ее зарядов в основном сосредоточено внутри молекулы и за ее пределами резко убывает. При взаимодействии двух молекул одновременно проявляются и силы притяжения и силы отталкивания, они по-разному зависят от расстояния между молекулами (см рис.- пунктирные линии). Одновременное действие межмолекулярных сил дает зависимость силы F от расстояния r между молекулами, характерную и для двух молекул, и атомов, и ионов (сплошная кривая). На больших расстояния молекулы практически не взаимодействуют, на очень малых расстояния преобладают силы отталкивания. На расстояниях, равных нескольким диаметрам молекул действуют силы притяжения. Расстояние ro между центрами двух молекул, на котором F=0, - это положение равновесия. Так как сила связана с потенциальной энергией F=-dEпот /dr, то интегрирование даст зависимость потенциальной энергии от r (потенциальная кривая). Равновесное положение соответствует минимуму потенциальной энергии - Umin. Для различных молекул вид потенциальной кривой аналогичен, но числовые значения ro и Umin различны и определяются природой данных молекул.


