
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 6. Закон сохранения механической энергии.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Закон сохранения механической энергии:«Если система: 1)система замкнута (не действуют внешние силы), 2)система консервативна (не действуют силы трения, сопротивления), то полная механическая энергия системы остается постоянной»: Вопрос 7. Законы сохранения применительно к абсолютно упругому удару двух шаров. Абсолютно упругий удар – это такой удар, при котором сохраняется кинетическая энергия всей системы.
Вопрос 8. Законы сохранения применительно к абсолютно неупругий удару двух шаров. Абсолютно неупругий - это удар, при котором тела после удара движутся как единое целое, и часть механической энергии переходит в теплоту.
(8, 9)Тема 8. ДИНАМИКА АТТ. Вопрос 1. Момент силы. Момент импульса. Основной закон динамики вращательного движения.
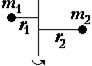
Вопрос 2. Момент инерции. Сформулировать теорему Штейнера. Величина I называется моментом инерции тела – это скалярная величина - по смыслу момент инерции является мерой инертности тела при вращательном движении. Моменты инерции – это аддитивные величины, т. е. для нескольких точек при одной и той же оси они просто складываются. материальной точки: системы материальных точек: абсолютно твердого тела:
Вопрос 3. Получить выражение для момента инерции.
Вопрос 4. Основной закон динамики для вращения тела вокруг неподвижной оси.
Вопрос 5. Плоские движения твердого тела. При плоском движении каждая точка тела в процессе движения остается все время в одной и той же плоскости. В этом случае ось вращения не меняет своего положения по отношению к телу, и уравнения упрощаются, т.е. для поступательного движения достаточно двух осей проекций х и у,а для вращательного - одной оси z. При этом говорят, что «ось вращения неподвижна» (по отношению к телу). Для «неподвижной» оси вращения момент импульса можно записать в скалярном виде, учитывая связь линейной и угловой скоростей
Рассмотрим скатывание сплошного цилиндра с наклонной плоскости.
Вопрос 7. Кинетическая энергия при вращательном движении. Найдем выражение для кинетической энергии при вращении тела относительно неподвижной оси, учитывая, что АТТ - система материальных точек, а энергия аддитивная величина: Тема 9. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 940; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

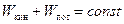 . Общефизический закон сохранения энергии: «Энергия не исчезает и не возникает вновь, она может только переходить из одной формы в другую».
. Общефизический закон сохранения энергии: «Энергия не исчезает и не возникает вновь, она может только переходить из одной формы в другую».


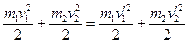




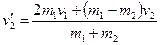
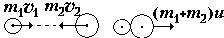

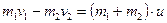




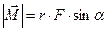 - момент силы относительно любой отсчетной точки O – это вектор, перпендикулярный плоскости, в которой лежат радиус-вектор и вектор силы.
- момент силы относительно любой отсчетной точки O – это вектор, перпендикулярный плоскости, в которой лежат радиус-вектор и вектор силы.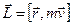
 - момент импульса относительно любой отсчетной точки О – это вектор, направленный перпендикулярно плоскости, в которой лежат радиус-вектор и вектор импульса точки.
- момент импульса относительно любой отсчетной точки О – это вектор, направленный перпендикулярно плоскости, в которой лежат радиус-вектор и вектор импульса точки.



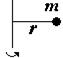



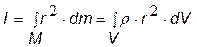
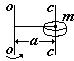 Теорема Штейнера: момент инерции I относительно произвольной оси равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями: I=Ic+ma2.
Теорема Штейнера: момент инерции I относительно произвольной оси равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями: I=Ic+ma2.



 основной закон динамики вращательного движения при неподвижной оси вращения (II закон Ньютона для вращательного движения), w - угловая скорость, e - угловое ускорение.
основной закон динамики вращательного движения при неподвижной оси вращения (II закон Ньютона для вращательного движения), w - угловая скорость, e - угловое ускорение.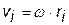 :
: .
.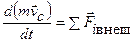



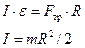

 Вопрос 6. Работа и мощность при вращательном движении.
Вопрос 6. Работа и мощность при вращательном движении.


 ,отсюда работа при вращательном движении
,отсюда работа при вращательном движении  .Мощность при вращат. движении
.Мощность при вращат. движении  .
. .Кинетическая энергия тела при вращении относительно неподвижной оси. Если тело одновременно движется и поступательно и вращается, то его кинетическая энергия складывается из двух частей:
.Кинетическая энергия тела при вращении относительно неподвижной оси. Если тело одновременно движется и поступательно и вращается, то его кинетическая энергия складывается из двух частей: 
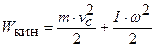 , v c – скорость центра масс.
, v c – скорость центра масс.


