
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 5. Центр масс(центр инерции). Уравнение движения центра масс.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Центром масс (центром инерции) называется воображаемая точка, в которой как бы сосредоточена вся масса тела или системы тел. Центр тяжести практически совпадает с центром масс.
Тема 6. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА. Вопрос 1. Замкнутая и незамкнутая системы в механике. Закон сохранения импульса. Система, на которую не действуют внешние силы или их действие скомпенсировано, т.е. для которой Пространство однородно – это означает, что все точки пространства эквивалентны, т.е. равноправны. В однородном пространстве нет каких-либо особых точек, отличных от других. Если некоторую систему тел перенести в другое место пространства, а тела в ней поставить в те же условия, в которых они находились в прежнем положении, то это никак не отразится на ходе всех последующих явлений. Если взять замкнутую систему тел, для которой полный импульс системы равен некоторой величине, то и в любом другом месте полный импульс будет оставаться тем же самым. Иначе говоря, закон сохранения импульса является следствием однородности пространства. Тема 7. РАБОТА. МОЩНОСТЬ. ЭНЕРГИЯ. Вопрос 1. Определение элементарной работы, различные выражения.
Вопрос 2. Мощность, ее выражение через силу и скорость тела. Мощность (Дж/с = Вт) – по смыслу – это работа, совершаемая за единицу времени.
Используя выражение для работы, мощность можно выразить как скалярное произведение вектора силы и вектора скорости: Вопрос 3. Кинетическая энергия и ее выражение через импульс тела. Кинетическая энергия – это энергия, связанная с движением. Выражение для кинетической энергии можно получить, если найти работу, которую должна совершить сила F, чтобы сообщить неподвижному телу массой m скорость v.
Вопрос 4. Консервативные силы, их работа. Потенциальная энергия. Консервативные (потенциальные) силы - силы, которые зависят только от координат тела и не зависят от его скорости. Работа консервативных сил (силы тяготения (тяжести), упругости, электростатические) не зависит от формы пути и определяется только начальным и конечным положением тела. Работа таких сил по замкнутому пути равна нулю. Т.е., каждую точку поля можно однозначно охарактеризовать работой, производимой при перемещении из некоторой условно нулевой точки в данную точку. Величина этой работы, взятая с обратным знаком, яв-ляется потенциальной энергией. Потенциальная энергия вводится только для консервативных систем. Вопрос 5. Диссипативные силы, их работа. Кинетическая энергия механической системы. Диссипативные силы всегда направлены противоположно скорости тела, они зависят от скорости тела, а также от других факторов. Диссипативные силы: силы сухого трения, сопротивления (вязкого трения), силы неупругой деформации. Изменение кинетической энергии системы материальных точек равно алгебраической сумме работ всех сил, действующих на систему.
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 552; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.158.111 (0.009 с.) |

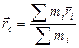
 Перепишем первое уравнение, дифференцируя, найдем скорость центра масс и получим:
Перепишем первое уравнение, дифференцируя, найдем скорость центра масс и получим: 

 .
.  - уравнение движения центра масс.
- уравнение движения центра масс. , называется замкнутой или изолированной. Для такой системы можно записать:
, называется замкнутой или изолированной. Для такой системы можно записать:  и, т.к.
и, т.к.  , следовательно,
, следовательно,  - закон сохранения импульса: «В замкнутой системе полный импульс материальных точек остается постоянным».
- закон сохранения импульса: «В замкнутой системе полный импульс материальных точек остается постоянным».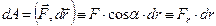 -элементарная работа, т.е. работа, совершаемая при таком малом перемещении, в пределах которого силу можно считать неизменной, Fr - проекция силы на направление перемещения.
-элементарная работа, т.е. работа, совершаемая при таком малом перемещении, в пределах которого силу можно считать неизменной, Fr - проекция силы на направление перемещения.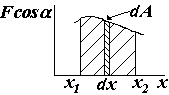
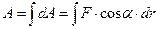 - полная работа (это всегда интеграл).
- полная работа (это всегда интеграл).  ,только при
,только при  , a = 0 и S = D r.
, a = 0 и S = D r. 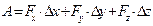 -работа на конечном участке, выраженная через проекции силы и изменения координат.
-работа на конечном участке, выраженная через проекции силы и изменения координат. На приведенном графике для одномерного движения - работа – площадь под кривой зависимости проекции силы от перемещения х. Работа является положительной, если сила действует в сторону перемещения (перпендикулярная сила работы не совершает).
На приведенном графике для одномерного движения - работа – площадь под кривой зависимости проекции силы от перемещения х. Работа является положительной, если сила действует в сторону перемещения (перпендикулярная сила работы не совершает). .
.



 Таким образом, неподвижное тело за счет работы силы приобрело скорость и кинетическую энергию.
Таким образом, неподвижное тело за счет работы силы приобрело скорость и кинетическую энергию. «Работа консервативных сил равна убыли потенциальной энергии тела».
«Работа консервативных сил равна убыли потенциальной энергии тела».




