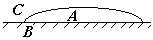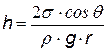Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
внутренняя энергия идеального газаСодержание книги Поиск на нашем сайте (приведена для сравнения)
Рассмотрим теперь расширение идеального и реального газов в вакуум.
будет адиабатически (dQ = 0) расширяться в пустоту, где внешнее давление рвнеш = 0 и, следовательно, работа dA = 0, т.е. расширяясь, газ не совершает работу. Согласно I началу термодинамики: dU = - dA = 0. Таким образом, внутренняя энергия идеального газа и, соответственно, температура газа остаются постоянными: U = const, T = const Рассуждая аналогично, для реального газа получим:
Явление изменения температуры газа при его расширении от давления р 1 до давления р 2 называется эффектом Джоуля - Томсона, по имени ученых которые впервые его наблюдали. Для большинства газов при комнатной температуре температура газа понижается, а для водорода и гелия повышается. Это можно объяснить тем, что в действительности газ расширяется не в вакуум, а от давления р 1 до давления р 2, т.е. совершается работа сначала внешними силами, а затем против внешних сил и
У различных газов при различных начальных объеме и температуре в большей или меньшей степени может сказываться роль взаимодействия молекул между собой или их собственный объем. Даже для одного и того же газа в зависимости от начальных условий Т 1 и V 1 изменение температуры при расширении может быть > 0 или < 0. Начальная температура, при которой происходит перемена знака в эффекте Джоуля – Томсона, называется температурой инверсии. Эффект Джоуля – Томсона используется для получения низких температур. При транспортировке газа по трубам при резком сужении диаметра трубы может понизиться температура газа, а при наличии в нем влаги образуются гидраты – снегоподобные вещества, которые могут закупорить трубу. Тема 18. Вопрос 2. ЖИДКОСТИ Жидкости по своему строению занимают промежуточное положение между газами и твердыми телами. Однако, по структуре они все же ближе к твердым телам. Так, рентгенограмма воды схожа с рентгенограммой льда, она показывает наличие некоторой упорядоченности в молекулярной структуре воды. Вблизи данной молекулы группируется определенное количество других молекул, причем существует определенный порядок в их расположении. Чем дальше от данной молекулы, тем беспорядоченнее располагаются другие молекулы по отношению к данной. В жидкости вследствие теплового движения молекулы некоторое время колеблются около положений равновесия, а затем перескакивают в новое положение равновесия. По образному выражению Френкеля молекулы жидкости ведут «оседло-кочевой образ жизни». Если теория газов достаточно хорошо развита и может объяснить большинство наблюдаемых их свойств, квантовая теория твердых тел тоже достигла больших успехов, то теория жидкого состояния далека еще от завершения. Основные особенности жидкого состояния. 1) Жидкости сохраняют свой объем, но не имеют определенной формы. 2) Жидкости практически несжимаемы. Из-за сильного взаимодействия молекул между собой, они сами себя как бы сжимают. Внутреннее давление, возникающее из-за взаимодействия молекул, очень велико. Например, для воды порядка 17000 атм, для ртути порядка 40000 атм. Это свойство жидкостей используется в гидравлических устройствах: подъемниках, прессах, тормозных устройствах. 3) С увеличением температуры увеличивается объем жидкости. Исключение составляет вода, объем которой в интервале (0 ¸ 4) оС уменьшается за счет ассоциации молекул в группы. 4) Наличие поверхностного натяжения на границе жидкости. Поверхностное натяжение. На молекулу жидкости действуют силы притяжения со стороны окружающих молекул. Если молекула находится внутри жидкости, эти силы уравновешены. Если молекула находится вблизи поверхности, то возникает сила, направленная внутрь жидкости. Поэтому, чтобы извлечь молекулу из глубины на поверхность, т.е. увеличить поверхность жидкости, требуется совершить работу. Эта работа пропорциональна увеличению площади поверхности: dA ~ dS. Вводя коэффициент пропорциональности s, можно записать:
s называется коэффициентом поверхностного натяжения. По смыслу он представляет собой работу, которую надо совершить, чтобы увеличить площадь поверхности на единицу при постоянной температуре. Это так называемый энергетический смысл s. Молекулы на поверхности обладают дополнительной потенциальной энергией. Любая система стремится перейти в состояние с наименьшей потенциальной энергией, поэтому поверхность жидкости стремится приобрести форму с наименьшей площадью поверхности. Небольшие объемы жидкости приобретают круглую форму (у шара наименьшая площадь поверхности).
Из этой формулы коэффициент поверхностного натяжения можно определить так: s численно равен силе, действующей по касательной к поверхности жидкости, в расчете на единицу длины раздела поверхности. Поверхностное натяжение жидкостей прив одит к явлению, называемому смачиванием. На рис. показано, какую форму может принимать капля одной и той же жидкости на разных поверхностях. Угол q между касательными, проведенными к поверхности жидкости и твердого тел, называется краевым углом смачивания.
Почему одна и та же жидкость может быть смачивающей или несмачивающей, можно объяснить с помощью приведенного рисунка. Обозначим молекулы жидкости символически буквой A, молекулы вещества подложки – B и молекулы окружающего воздуха или паров жидкости - C, силы их взаимодействия, соответственно, FAA, FAB FBB,… Силы FBС и FАС, << FAA и FВВ, т.к. концентрация молекул С (газ) по сравнению с концентрациями молекул А и В пренебрежимо мала (это конденсированные среды). Если силы FAB > FAA, жидкость будет смачивать поверхность, если FAB < FAA, будет наблюдаться несмачивание. Явление смачивания играет большую роль в природе и технике. Например, при обогащении руд методом флотации в породу вводят специальные вещества, которые обволакивают ценную руду, делая ее несмачиваемой для воды. Пузырьки воздуха, подаваемого в раствор, пристают к к кусочкам руды, и порода всплывает. Вопрос 3. Смачивание приводит к тому, что на стенках сосуда жидкость как бы «ползет» по стенке, и ее поверхность искривляется. В широком сосуде это искривление практически незаметно. В узких трубках – капиллярах – этот эффект можно наблюдать визуально. За счет сил поверхностного натяжения создается дополнительное (по сравнению с атмосферным) давление Dр, направленное к центру кривизны поверхности жидкости.
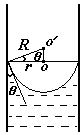
Дополнительное давление вблизи искривленной поверхности жидкости D р приводит к подъему (при смачивании) или опусканию (при несмачивании) жидкости в капиллярах. При равновесии дополнительное давление равно гидростатическому давлению столбика жидкости. Из формулы Лапласа для капилляра круглого сечения D p = 2s / R, гидростатическое давление р = r g h. Приравнивая Dр = р, найдем h.
Из формулы видно, что чем меньше радиус капилляра, тем выше подъем (или опускание) жидкости. Явление капиллярности чрезвычайно распространено в природе и технике. Например, проникновение влаги из почвы в растения осуществляется посредством подъема ее по капиллярным каналам. К капиллярным явлениям относится также такое явление, как движение влаги по стенам помещения, приводящее к сырости. Очень большую роль капиллярность играет при добыче нефти. Размеры пор в породе, содержащей нефть, чрезвычайно малы. Если добываемая нефть окажется несмачивающей по отношению к породе, то она закупорит канальца, и извлечь ее будет очень трудно. Добавляя к жидкости некоторые вещества даже в очень малом количестве, можно существенно изменить ее поверхностное натяжение. Такие вещества называются поверхностно-активными веществами. [1] N! =1×2×3××× N - факториал – это произведение целых чисел [2] Термодинамические законы не применимы к 3 молекулам. Пример взят для простоты вычислений. [3] Фаза – это совокупность частей системы, обладающих одинаковым химическим составом и находящихся в одинаковом состоянии.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 542; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 Пусть в сосуде 1 находится идеальный газ, а в сосуде 2 – вакуум (см. рис). Если теплоизолировать систему и открыть кран, то газ
Пусть в сосуде 1 находится идеальный газ, а в сосуде 2 – вакуум (см. рис). Если теплоизолировать систему и открыть кран, то газ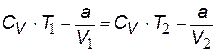
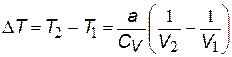
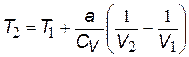
 . Если выразить давление из уравнения Ван-дер-Ваальса, то получим более общее выражение для изменения температуры газа при расширении, в которые входят поправки на взаимодействие молекул (а) и их собственный объем (b):
. Если выразить давление из уравнения Ван-дер-Ваальса, то получим более общее выражение для изменения температуры газа при расширении, в которые входят поправки на взаимодействие молекул (а) и их собственный объем (b):
 (Дж/м2)
(Дж/м2)
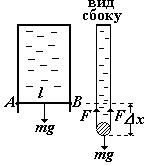 Коэффициенту поверхностного натяжения можно придать также силовой смысл. Пусть на проволочном каркасе с подвижной стороной АВ = l образована тонкая пленка жидкости (см. рис.). Под действием груза массой m пленка растянулась на Dх,при этом сила тяжести совершила работу DА = mg×Dх = 2 F×Dх Дальнейшему растяжению препятствуют силы поверхностного натяжения F. Подставим в формулу и получим:
Коэффициенту поверхностного натяжения можно придать также силовой смысл. Пусть на проволочном каркасе с подвижной стороной АВ = l образована тонкая пленка жидкости (см. рис.). Под действием груза массой m пленка растянулась на Dх,при этом сила тяжести совершила работу DА = mg×Dх = 2 F×Dх Дальнейшему растяжению препятствуют силы поверхностного натяжения F. Подставим в формулу и получим:  . Таким образом
. Таким образом (Н/м)
(Н/м)