

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Кинематика материальной точки и поступательного
Содержание книги
- Наука – это особая сфера духовной, а именно интеллектуальной деятельности человека и человечества, целью которой является выработка достоверного знания об окружающей нас действительности.
- Кинематика материальной точки и поступательного
- Основные законы динамики (Ньютон, 1687г.)
- Энергия – универсальная, количественная мера различных форм движения и взаимодействия: она характеризует способность физических тел или систем совершить движение.
- Полная механическая энергия замкнутой системы тел, в которой действуют только консервативные силы, сохраняется, не изменяется со временем.
- Механика вращательного движения
- Скорость изменения момента импульса вращающегося тела определяется суммарным моментом сил, действующих на это тело.
- Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.
- Обратимый процесс есть идеализированная модель реальных процессов, необходимая для успешного изучения последних.
- Энергетические характеристики электрического поля
- Энергия электростатического поля
- Плотность тока пропорциональна напряженности электрического поля и имеет одинаковое с ней направление.
- Алгебраическая сумма сил тока в узле разветвления равна нулю.
- Рукоятка буравчика, ввинчиваемого по направлению тока, вращается в направлении магнитных силовых линий.
- Индуктивность, самоиндукция, взаимная индукция
- Закон независимости световых пучков: пучки световых лучей, пересекаясь, не взаимодействуют и распространяются после пересечения независимо друг от друга.
- Аберрации или погрешности оптических систем
- Сравнительный анализ параметров интерференции и дифракции
- С точки зрения волновой теории
- Закономерности излучения абсолютно черного тела
- Распределение электронов в атоме по состояниям
- Закон радиоактивного распада
- Выделение ядерной энергии происходит как при реакциях деления тяжелых ядер, так и при реакциях синтеза легких ядер.
- Элементарные частицы это такие микрочастицы, внутреннюю структуру которых, на современном уровне развития физики, нельзя представить как объединение других, более мелких частиц
- Волновые свойства микрочастиц
- Соотношение неопределенности является квантовым ограничением применимости классической механики к микрообъектам.
- Трофимова Т.И., Курс физики, «Высшая школа»,2000г.
- Применение первого начала термодинамики к термодинамическим изопроцессам
Похожие статьи вашей тематики
Движения твердого тела
Движение физических тел (или материальных точек) происходит в пространстве и во времени. Любое перемещение тела относительно, поэтому, чтобы описать его, надо изучить и выбрать систему отсчета – совокупность системы координат и часов, в отношении которой происходит изменение положения тел в течение времени. Такой наиболее часто используемой системой является декартова система координат, где оси координат взаимно перпендикулярны. Положение любой точки А в данный момент времени характеризуется тремя координатами x, y и z или радиус-вектором 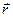 , проведенным из начала системы координат в данную точку (рис 4). , проведенным из начала системы координат в данную точку (рис 4).
 Функции зависимости координат от времени: x=x(t); y=y(t); z=z(t) или Функции зависимости координат от времени: x=x(t); y=y(t); z=z(t) или 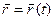 , называются кинематическими уравнениями движения материальной точки. , называются кинематическими уравнениями движения материальной точки.
Траектория движения материальной точки – линия, описываемая этой точкой в пространстве, – может быть прямолинейной или криволинейной.
 При движении материальной точки вдоль произвольной траектории, длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени (когда она находилась в положении А и характеризовалась радиус-вектором При движении материальной точки вдоль произвольной траектории, длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени (когда она находилась в положении А и характеризовалась радиус-вектором  ), называется длиной пути ), называется длиной пути 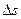 и является скалярной функцией времени: и является скалярной функцией времени: 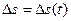 (рис.5). Вектор (рис.5). Вектор  , проведенный из начального положения движущейся точки в ее положение В в данный момент времени (характеризующийся радиус-вектором , проведенный из начального положения движущейся точки в ее положение В в данный момент времени (характеризующийся радиус-вектором  ), называется перемещением. Иными словами, векторная величина перемещение – это приращение радиус-вектора точки за рассматриваемый промежуток времени. ), называется перемещением. Иными словами, векторная величина перемещение – это приращение радиус-вектора точки за рассматриваемый промежуток времени.
Для количественной характеристики движения тела вводится понятие скорости движения. В обыденной жизни под скоростью понимают путь, проходимый телом или частицей за единицу времени. Если за равные, сколь угодно малые промежутки времени тело проходит одинаковые пути, движение тела называют равномерным. В этом случае скорость, которой обладает тело в каждый момент времени, можно вычислить, разделив путь s на время t. Если тело движется прямолинейно и не меняет направление движения, то путь движения 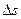 и модуль перемещения и модуль перемещения  совпадают совпадают  = = 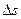 . Тогда движение тела можно характеризовать средней скоростью (средняя путевая скорость), которая является скалярной величиной: . Тогда движение тела можно характеризовать средней скоростью (средняя путевая скорость), которая является скалярной величиной:  , отсюда следует, что единица измерения скорости метр в секунду (м/с). , отсюда следует, что единица измерения скорости метр в секунду (м/с).
В физике под скоростью понимают векторную величину, характеризующую не только быстроту перемещения тела по траектории, но и направление, в котором движется это тело в каждый момент времени, поэтому существует и другое определение средней скорости – средняя скорость перемещения, которая является векторной величиной.
Под средней скоростью перемещения 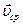 понимают отношение перемещения понимают отношение перемещения  , пройденного телом или материальной точкой, к промежутку времени , пройденного телом или материальной точкой, к промежутку времени 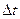 , за которой этот путь пройден: , за которой этот путь пройден:  . .
Для неравномерного и криволинейного движения 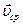 не всегда позволяет определить, даже приблизительно, реальные скорости на пути движения. Например, когда тело, двигаясь криволинейно, возвращается в исходное положение, то у него не всегда позволяет определить, даже приблизительно, реальные скорости на пути движения. Например, когда тело, двигаясь криволинейно, возвращается в исходное положение, то у него 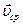 =0, так как его перемещение =0, так как его перемещение  =0, но средняя путевая скорость =0, но средняя путевая скорость  , так как путь движения , так как путь движения 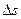 ≠0. Такое двоякое определение средней скорости приводит к тому, что в каждом конкретном случае следует различать эти два определения средней скорости и точно знать, о какой из них идет речь в данной задаче. ≠0. Такое двоякое определение средней скорости приводит к тому, что в каждом конкретном случае следует различать эти два определения средней скорости и точно знать, о какой из них идет речь в данной задаче.
Но существуют задачи, для решения которых средняя скорость недостаточна и вводится понятие мгновенной скорости, которое характеризует движение тела в данной точке траектории и в данный момент времени. Мгновенная скорость (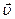 ) в любой точке траектории есть вектор, направленный по касательной к траектории, а по модулю равный пределу средней скорости перемещения при стремлении промежутка времени к нулю. ) в любой точке траектории есть вектор, направленный по касательной к траектории, а по модулю равный пределу средней скорости перемещения при стремлении промежутка времени к нулю.
 Мгновенная скорость Мгновенная скорость  . .
Модуль скорости равен производной пути по времени:

Из рис. 5 видно, что всегда 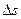 ≥ ≥  , но при Δt→0, , но при Δt→0,  → →  и dr=ds (рис.6). По этому из определения мгновенной скорости находим, что и dr=ds (рис.6). По этому из определения мгновенной скорости находим, что  или или  . При прямолинейном и равномерном движении ( . При прямолинейном и равномерном движении (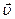 =const) длина пути s=υ(t2 − t1)=υ· =const) длина пути s=υ(t2 − t1)=υ· 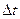 , а координаты, например, x=x0+υx , а координаты, например, x=x0+υx 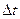 , где , где  - проекция скорости на оси х. Аналогично определяются и координаты y=y0+υyΔt и z=z0+υz Δt. - проекция скорости на оси х. Аналогично определяются и координаты y=y0+υyΔt и z=z0+υz Δt.

Ускорение – физическая величина, характеризующая быстроту изменения скорости по модулю и по направлению (рис.7). Здесь определяют среднее ускорение ( ) как отношение изменения скорости к промежутку времени, за который это изменение произошло, и мгновенное ускорение ( ) как отношение изменения скорости к промежутку времени, за который это изменение произошло, и мгновенное ускорение ( ) как предел среднего ускорения при Δt → 0, т.е. производной скорости по времени. ) как предел среднего ускорения при Δt → 0, т.е. производной скорости по времени.
 и и  = =  , отсюда следует, что ускорение выражается в метрах на секунду в квадрате (м/c2). , отсюда следует, что ускорение выражается в метрах на секунду в квадрате (м/c2).
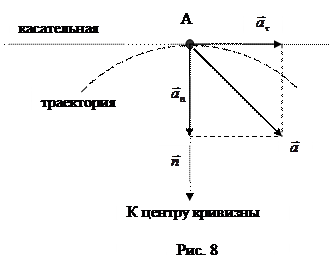 Целесообразно раскладывать вектор ускорения на две составляющие, одна из которых направлена по касательной к траектории и называется касательным или тангенциальным ускорением ( Целесообразно раскладывать вектор ускорения на две составляющие, одна из которых направлена по касательной к траектории и называется касательным или тангенциальным ускорением (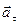 ), а другая – по нормали к траектории и называется нормальным или центростремительным ускорением ( ), а другая – по нормали к траектории и называется нормальным или центростремительным ускорением ( ) (рис. 8). Ускорение и его составляющие связаны между собой очевидными соотношениями: ) (рис. 8). Ускорение и его составляющие связаны между собой очевидными соотношениями:  = = 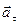 + +  и и  . .
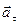 - тангенциальное ускорение, направленное по касательной, определяет быстроту изменения модуля скорости. Его модуль равен производной модуля скорости по времени или второй производной пути по времени, - тангенциальное ускорение, направленное по касательной, определяет быстроту изменения модуля скорости. Его модуль равен производной модуля скорости по времени или второй производной пути по времени,  (рис.9). (рис.9).
 - нормальное (центростремительное) ускорение характеризует изменение скорости по направлению. Оно направлено к центру кривизны вдоль радиуса кривизны в данной точке траектории ( - нормальное (центростремительное) ускорение характеризует изменение скорости по направлению. Оно направлено к центру кривизны вдоль радиуса кривизны в данной точке траектории (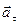   ). Модуль нормального ускорения ). Модуль нормального ускорения  , где R -радиус кривизны. Действительно, при Δt→0, B→A (рис.10), траекторию можно принять как окружность с радиусом R. ΔS=AB и из ΔAOB~ΔDAE имеем , где R -радиус кривизны. Действительно, при Δt→0, B→A (рис.10), траекторию можно принять как окружность с радиусом R. ΔS=AB и из ΔAOB~ΔDAE имеем  , но AB=ΔS=υ·Δt, тогда , но AB=ΔS=υ·Δt, тогда  так как при Δt→0, υ1→υ. так как при Δt→0, υ1→υ.
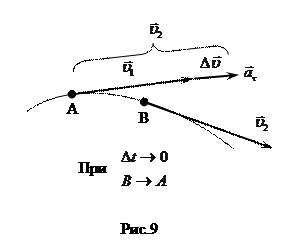 
В табл.1 представлены виды движения в зависимости от различных значений тангенциальных и нормальных ускорений, а на рис.11 − графики зависимости пути s, скорости υ и ускорения a от времени t при равноускоренном движении без начальной скорости (а), υ0=0) и с начальной скоростью (б), υ0≠0).
Таблица 1. Виды движения
| №
| Полное ускорение  = =  = = 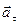 + + 
| |
|  =0; =0;  =0 =0
| Прямолинейное, равномерное движение
 , длина пути s= , длина пути s=  = υ ·Δt = υ ·Δt
| |
|  = а= const; = а= const;
 =0 =0
| Прямолинейное, равнопеременное движение
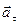 = а= = а=  , если t1=0, υ1= υ0 , то υ=υo+at , если t1=0, υ1= υ0 , то υ=υo+at

| |
|  = =  (t); (t);  =0 =0
| Прямолинейное движение с переменным ускорением
 , , 
| |
|  =0; =0;  =const =const
| Равномерное движение по окружности,
скорость по модулю не меняется (d υ =0),
 меняется по направлению,
из an= υ2 /R следует, что R=const меняется по направлению,
из an= υ2 /R следует, что R=const
| |
|  =0; =0;  ≠0 ≠0
| Равномерное, криволинейное движение
| |
|  =const; =const;  ≠0 ≠0
| Криволинейное, равнопеременное движение
| |
|  = =  (t); (t);  ≠0 ≠0
| Криволинейное движение с переменным ускорением
|
|



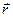 , проведенным из начала системы координат в данную точку (рис 4).
, проведенным из начала системы координат в данную точку (рис 4). Функции зависимости координат от времени: x=x(t); y=y(t); z=z(t) или
Функции зависимости координат от времени: x=x(t); y=y(t); z=z(t) или 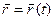 , называются кинематическими уравнениями движения материальной точки.
, называются кинематическими уравнениями движения материальной точки. При движении материальной точки вдоль произвольной траектории, длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени (когда она находилась в положении А и характеризовалась радиус-вектором
При движении материальной точки вдоль произвольной траектории, длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени (когда она находилась в положении А и характеризовалась радиус-вектором  ), называется длиной пути
), называется длиной пути 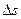 и является скалярной функцией времени:
и является скалярной функцией времени: 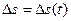 (рис.5). Вектор
(рис.5). Вектор  , проведенный из начального положения движущейся точки в ее положение В в данный момент времени (характеризующийся радиус-вектором
, проведенный из начального положения движущейся точки в ее положение В в данный момент времени (характеризующийся радиус-вектором  ), называется перемещением. Иными словами, векторная величина перемещение – это приращение радиус-вектора точки за рассматриваемый промежуток времени.
), называется перемещением. Иными словами, векторная величина перемещение – это приращение радиус-вектора точки за рассматриваемый промежуток времени. совпадают
совпадают  , отсюда следует, что единица измерения скорости метр в секунду (м/с).
, отсюда следует, что единица измерения скорости метр в секунду (м/с).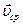 понимают отношение перемещения
понимают отношение перемещения  , пройденного телом или материальной точкой, к промежутку времени
, пройденного телом или материальной точкой, к промежутку времени 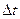 , за которой этот путь пройден:
, за которой этот путь пройден:  .
. , так как путь движения
, так как путь движения 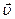 ) в любой точке траектории есть вектор, направленный по касательной к траектории, а по модулю равный пределу средней скорости перемещения при стремлении промежутка времени к нулю.
) в любой точке траектории есть вектор, направленный по касательной к траектории, а по модулю равный пределу средней скорости перемещения при стремлении промежутка времени к нулю. Мгновенная скорость
Мгновенная скорость  .
.
 , но при Δt→0,
, но при Δt→0,  →
→  и dr=ds (рис.6). По этому из определения мгновенной скорости находим, что
и dr=ds (рис.6). По этому из определения мгновенной скорости находим, что  или
или  . При прямолинейном и равномерном движении (
. При прямолинейном и равномерном движении ( - проекция скорости на оси х. Аналогично определяются и координаты y=y0+υyΔt и z=z0+υz Δt.
- проекция скорости на оси х. Аналогично определяются и координаты y=y0+υyΔt и z=z0+υz Δt.
 ) как отношение изменения скорости к промежутку времени, за который это изменение произошло, и мгновенное ускорение (
) как отношение изменения скорости к промежутку времени, за который это изменение произошло, и мгновенное ускорение ( ) как предел среднего ускорения при Δt → 0, т.е. производной скорости по времени.
) как предел среднего ускорения при Δt → 0, т.е. производной скорости по времени. и
и  =
=  , отсюда следует, что ускорение выражается в метрах на секунду в квадрате (м/c2).
, отсюда следует, что ускорение выражается в метрах на секунду в квадрате (м/c2). Целесообразно раскладывать вектор ускорения на две составляющие, одна из которых направлена по касательной к траектории и называется касательным или тангенциальным ускорением (
Целесообразно раскладывать вектор ускорения на две составляющие, одна из которых направлена по касательной к траектории и называется касательным или тангенциальным ускорением (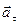 ), а другая – по нормали к траектории и называется нормальным или центростремительным ускорением (
), а другая – по нормали к траектории и называется нормальным или центростремительным ускорением ( ) (рис. 8). Ускорение и его составляющие связаны между собой очевидными соотношениями:
) (рис. 8). Ускорение и его составляющие связаны между собой очевидными соотношениями:  .
. (рис.9).
(рис.9).
 , где R -радиус кривизны. Действительно, при Δt→0, B→A (рис.10), траекторию можно принять как окружность с радиусом R. ΔS=AB и из ΔAOB~ΔDAE имеем
, где R -радиус кривизны. Действительно, при Δt→0, B→A (рис.10), траекторию можно принять как окружность с радиусом R. ΔS=AB и из ΔAOB~ΔDAE имеем  , но AB=ΔS=υ·Δt, тогда
, но AB=ΔS=υ·Δt, тогда  так как при Δt→0, υ1→υ.
так как при Δt→0, υ1→υ.


 =0;
=0;  =0
=0
 , длина пути s=
, длина пути s=  = υ ·Δt
= υ ·Δt
 , если t1=0, υ1= υ0 , то υ=υo+at
, если t1=0, υ1= υ0 , то υ=υo+at

 ,
, 
 меняется по направлению,
из an= υ2 /R следует, что R=const
меняется по направлению,
из an= υ2 /R следует, что R=const



