
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соотношение неопределенности является квантовым ограничением применимости классической механики к микрообъектам.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Принцип неопределенности, отражая физическую реальность, доказывает вероятностный характер физических характеристик микрочастиц: ее координат, импульса, энергии и др.. Примеряя соотношение неопределенности к электрону в атоме водорода, получаем, что его неопределенность скорости вращения вокруг ядра в несколько раз больше самой скорости, т.е. в данном случае нельзя говорить о движении электрона в атоме по определенной траектории, иными словами, для описания движения электрона в атоме нельзя пользоваться законами классической физики. Поэтому понятие орбиты применяется к электрону только в боровском приближении, которое, кстати, в некоторых случаях давал вполне удовлетворительные результаты. В квантовой механике представление о точных значениях координаты, мгновенной скорости микрочастицы, ее траектории (в классическом понимании) теряет смысл. Однако, законы сохранения импульса, энергии в квантовой механике выполняются строго. В квантовой теории рассматриваются также соотношение неопределенности для энергии E и времени t, т.е. неопределенности этих величин удовлетворяют условию ΔE . Δt ≥ h, где ΔE - неопределенность энергии некоторого состояния системы, а Δt - промежуток времени, в течение которого оно существует. Это приводит к «размытию» спектральных линий, которое экспериментально наблюдается и при помощи которого можно оценить порядок времени существования атома в возбужденном состоянии. Естественно, энергетическая «размытость» метастабильных уравнений гораздо меньше, т.к. время жизни, и соответственно Δt на этих уровнях гораздо больше.
§3.9. Основы квантовой механики.
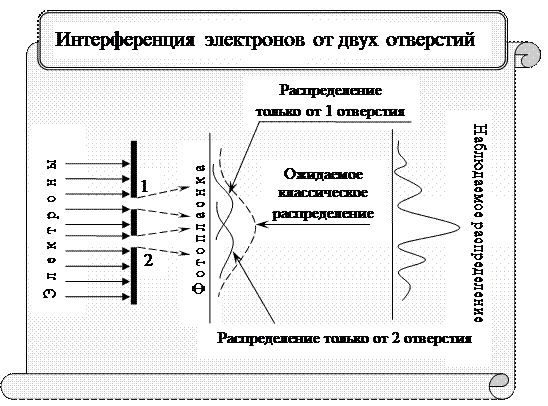
Таким образом, стало очевидным, что между процессами, совершающимися в макро- и микромире, существует не только количественное, но и качественное различие. Поэтому законы классической физики, полученные из наблюдений над макрообъектами, не всегда пригодны для описания процессов, происходящих в микромире. Для них используют результаты квантовой механики, физическими основами которой являются с одной стороны дискретность процессов микромира (кванты и фотоны) и волновая природа микрочастиц (волны де Бройля). При изучении квантовой физики определенные трудности составляют невозможность свести квантовые понятия и процессы к привычным представлениям и отсутствие в ряде случаев аналогий, столь облегчающих «понимание» изучаемого предмета. Иными словами, к сожалению, квантовая механика лишена наглядности, характерной для классической механики, и невозможно очевидными моделями представить или описать явления микромира. Из корпускулярно – волнового дуализма микрочастицы вытекает, что результаты, которые получаются из эксперимента, можно истолковать, используя с одной стороны выводы квантовой теории, и, с другой стороны, рассматривая частицу как волну с длиной де Бройля. Например, при дифракции электронов, освещенность дифракционной картины можно вычислить как результат интерференции волн де Бройля от разных электронов. Тогда, согласно волновым представлениям, интенсивность дифракционной картины пропорциональна квадрату амплитуды волны. По представлениям квантовой теории, интенсивность определяется числом электронов, попадающих в данную точку дифракционной картины. Следовательно, число электронов в данной точке дифракционной картины задается квадратом амплитуды волны де Бройля. Наличие максимумов в дифракционной картине с точки зрения волновой теории означает, что эти направления соответствуют наибольшей интенсивности волн де Бройля. С другой стороны, интенсивность волн де Бройля оказывается больше там, где имеется большее число частиц, попавших в эту точку или, иными словами, где больше вероятность попадания электронов. Таким образом, дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности, согласно которой частицы попадают в те места, где интенсивность волн де Бройля наибольшая.
Таким образом, в волновой теории интенсивность прямо пропорционально квадрату амплитуды A2, а согласно фотонной теории она прямо пропорционально числу фотонов n. Значит, n~A2. Для одного фотона A2 определяет вероятность попадания фотона в ту или иную точку. Этот пример показывает, что результаты квантовой теории имеют вероятностный характер и определяют вероятность того или иного события. Но волны де Бройля не могут играть роль волн вероятности, т.к. в каких то точках они имеют отрицательные значения. Для устранения этого Борн в 1926г. предположил, что по волновому закону меняется не сама вероятность, а величина ψ(x, y, z, t) − названная амплитудой вероятности или волновой функцией. Тогда вероятность W~|ψ(x, y, z, t)|2. Вероятность нахождения частицы в элементе объема dV: dW=~|ψ|2dV. |ψ|2 =dW/dV − имеет смысл плотности вероятности. Вероятность в объеме V: Нормировка Таким образом, движение микрочастиц в квантовой механике описывается принципиально по–новому − с помощью волновой функции ψ (x, y, z, t) (пси - функция), которая является основным носителем информации об их корпускулярных и волновых свойств. Физический смысл имеет не сама ψ – функция, а квадрат ее модуля |ψ|2, который характеризует вероятность пребывания частиц в данный момент времени, в определенной точке пространства, в данном объеме. Необходимость вероятного подхода к описанию микрочастиц является важнейшей отличительной особенностью квантовой теории. Вид функции ψ (x, y, z, t) в каждом конкретном случае получается решением волновой уравнения Шредингера (1926). Общее (основное) уравнение нерелятивистской квантовой механики, зависящим от времени:
где U − потенциальная энергия частицы в силовом поле. Уравнение Шредингера дополняется условиями, удовлетворяющие некоторые естественные требования к ψ − функции. ψ − функция должна быть: · конечной, однозначной и непрерывной во всем пространстве; · иметь непрерывные производные; · |ψ|2 должна быть интегрируемая: это приводит к ее нормировке (вероятность нахождения частицы где-либо в пространстве достоверное событие и равняется единице). Решение уравнения Шредингера, удовлетворяющие вышеуказанным требованиям (нахождение так называемых собственных функции ψ1, ψ2,…, ψn), возможно только при дискретных значениях полной энергии системы W (W1, W2, …, Wn ‑ энергетических уровнях). Отсюда и квантование не только энергии, но и других физических величин. Тогда квантовые числа естественным образом вытекают из решения уравнения Шредингера, а не постулируется, как в компромиссной теории Бора. Хотя само уравнение (как и все основные уравнения физики – как, например, уравнения Максвелла или уравнения Ньютона) не выводится, а постулируется, его правильность подтверждалась экспериментально. Уравнение Шредингера имеет бесчисленное множество решений, из которых посредством наложения граничных условий отбирают решения, имеющие физический смысл (более подробно в приложение).
Диаметры слоев у различных атомов различны. По мере увеличения заряда ядра диаметр внутренних слоев уменьшается (они как бы «подтягиваются» к ядру). Наружный слой – внешние размеры различных атомов (~10–10 м), меняется мало, благодаря экранизирующему действию внутренних слоев.
Приложение 1.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 826; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.69 (0.009 с.) |


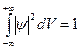

 − оператор Лапласа,
− оператор Лапласа,  ,
, ;
; Для электрона в атоме отдельная волновая функция определяет орбиталь, характеризуя распределение электронной плотности вокруг ядра (на рис. схематично показана зависимость вероятности обнаружения электрона от расстояния r до ядра). Максимум этой зависимости приходит на расстоянии r1 ≈ 0,53.10-10 м, которое соответствует радиусу первой боровской орбиты. Следовательно, электрон может быть обнаружен с наибольшей вероятностью на расстояниях, равных боровскому радиусу. Так как состояние электрона в этой орбитале сферически–симметричны, то электрон имеет наибольшую и одинаковую вероятность находиться во всех точках сферы радиусом r1 и с центром в ядре атома. Поэтому под орбиталью понимают область пространства, где вероятность пребывания электрона велика (~ 90 %). Каждому состоянию электрона в атоме соответствует своя орбиталь с характерными очертаниями и ориентацией. Такие задачи решаются в квантовой химии.
Для электрона в атоме отдельная волновая функция определяет орбиталь, характеризуя распределение электронной плотности вокруг ядра (на рис. схематично показана зависимость вероятности обнаружения электрона от расстояния r до ядра). Максимум этой зависимости приходит на расстоянии r1 ≈ 0,53.10-10 м, которое соответствует радиусу первой боровской орбиты. Следовательно, электрон может быть обнаружен с наибольшей вероятностью на расстояниях, равных боровскому радиусу. Так как состояние электрона в этой орбитале сферически–симметричны, то электрон имеет наибольшую и одинаковую вероятность находиться во всех точках сферы радиусом r1 и с центром в ядре атома. Поэтому под орбиталью понимают область пространства, где вероятность пребывания электрона велика (~ 90 %). Каждому состоянию электрона в атоме соответствует своя орбиталь с характерными очертаниями и ориентацией. Такие задачи решаются в квантовой химии.


