
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон независимости световых пучков: пучки световых лучей, пересекаясь, не взаимодействуют и распространяются после пересечения независимо друг от друга.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
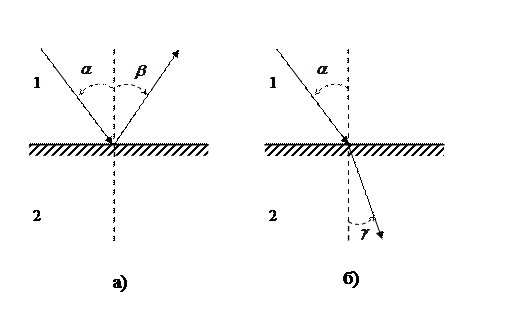
Луч света в однородной среде распространяется прямолинейно до тех пор, пока он не дойдет до границы этой среды с другой средой. На границе двух сред часть света (а в ряде случаев и весь свет) возвращается в первую среду (явление отражения света), а часть света проходить во вторую среду, меняя при этом направление своего распространения (явления преломления). В зависимости от свойств границы раздела между двумя средами, отражение может иметь различный характер. Если граница имеет вид поверхности, размеры неровностей которой меньше длины световой волны, то происходит зеркальное или направленное отражение, при котором узкие параллельные пучки света после отражения идут также по близким направлениям. Если же размеры неровностей больше длины волны света, то узкий пучок после отражения рассеивается по всевозможным направлениям (рассеянное или диффузное отражение). Законы зеркального отражения (левый рисунок, а)) 1. Падающий луч, отраженный луч и перпендикуляр к границе раздела двух сред, восставленный в точке падения луча, лежат в одной плоскости. 2. Угол отражения β равен углу падения α. Законы отражения справедливы при обратном направлении хода световых лучей. Луч, распространяющийся по пути отраженного, отражается по пути падающего луча (обратимость хода световых лучей)
Законы преломления (правый рисунок, б)) 1. Луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости. 2. Отношение синуса угла падения к синусу угла преломления есть постоянная для данных сред:
где n21 - относительный показатель преломления или показатель преломления второй среды относительно первой. Он равен отношению скоростей света в средах, на границе между которыми происходит преломление:
Показатель преломления среды относительно вакуума называют абсолютным показателем преломления этой среды. Относительный показатель преломления можно выразить через абсолютные показатели преломления n1 и n2 первой и второй сред:
Абсолютный показатель преломления для некоторых сред
Среду с меньшим абсолютным показателем преломления принято называть оптически менее плотной средой. В большинстве случаев (или если об этом специально не оговаривается) роль одной из сред играет воздух, оптические свойства которого мало отличается от таковых вакуума, поэтому абсолютный показатель преломления воздуха при нормальных условиях n ≈ 1. Следовательно, в таких случаях, n21 ≈n1≈n, поэтому в дальнейшем мы не будем разграничить абсолютные и относительные показатели преломления. Падающий и преломленный лучи тоже взаимно обратимы: если падающий луч будет пущен по направлению преломленного луча, то луч преломленный пойдет по направлению падающего.
Обычно для стекла n2≈ 1,5, поэтому αпр.= arcsin1/1,5≈420
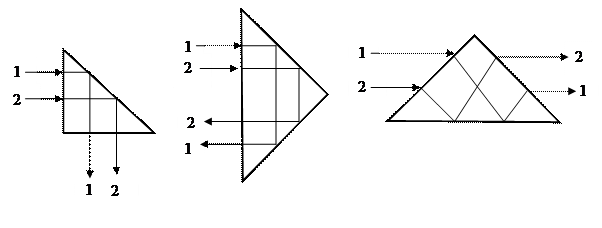
Тогда все лучи, которые попадают из стекла на границу стекло-воздух с углом больше чем 420, не могут выйти из стекла. Это дает возможность использовать прямоугольные призмы для того, чтобы повернуть луч на 900, повернуть изображение (например, в биноклях), обернуть лучи и т. п. Явления полного внутреннего отражения света сейчас находит широкое применение в волоконной оптике.
Формула призмы Призмой называется прозрачное тело, с двух сторон ограниченное плоскостями, которые составляют какой-то угол между собой (преломляющий угол призмы – θ, см. рисунок). После двукратного преломления (на левой и на правой гранях призмы) луч света отклоняется от первоначального направления на угол δ, называемый углом отклонения. Угол отклонения δ зависит от преломляющего угла θ и показателя преломления n призмы. Эта зависимость легко устанавливается для призмы с малым преломляющим углом (тонкая призма) в случаях малого угла падения α. δ ≈ (n -1)·θ (Вывести самостоятельно, учитывая, что при малых значениях θ и α, также малы углы γ, α1 и γ1, поэтому из закона преломления sin α= n.sin γ и n . sin α1=sinγ1 можно перейти к выражениям α= n γ и n α1= γ1, а θ=γ+α1, δ=(α-γ)+(γ1- α1)). Минимальный угол отклонения получается в случае симметричного хода луча (т.е. когда α=γ1 и луч внутри призмы параллелен основанию призмы). Обратите внимание, что при прохождении через призму луч всегда отклоняется в сторону основании.
§1.4. Линзы
Линзы – это прозрачные тела, ограниченные с двух сторон криволинейными (обычно сферическими) поверхностями, преломляющими световые лучи и способные формировать оптические изображения предметов. В частном случае одна из поверхностей может быть плоской
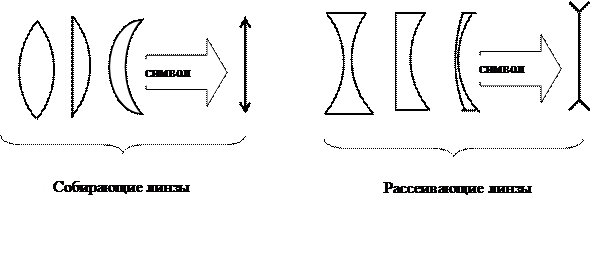
По внешней форме линзы делятся на двояковыпуклые, плосковыпуклые, вогнуто-выпуклые, двояковогнутые, плосковогнутые и выпукло-вогнутые (на рисунке они изображены слева направо). По оптическим свойствам линзы делятся на собирающие (положительные) и рассеивающие (отрицательные). Независимо от внешней формы собирающие линзы посредине толще, чем у краев, в то время, как рассеивающие линзы посредине тоньше, чем у краев.
Мы будем рассматривать тонкие линзы, толщина которых (расстояние АВ между ограничивающими поверхностями) значительно меньше по сравнению с расстоянием до предмета и с радиусами R1 и R2 поверхностей, ограничивающих линзу. В тонких линзах точки А и В расположены столь близко друг от друга, что можно принять их совпадающими с точкой О, называющимися оптическим центром линзы. Лучи света, проходящие через оптический центр линзы, практически не преломляются. Прямую О1О2, проходящую через центры (О1 и О2) сферических поверхностей и оптический центр линзы, называют главной оптической осью. Любую другую прямую, проходящую через оптический центр, называют побочной оптической осью (на рисунке О'1О'2). Линзу грубо можно представить как совокупность множества призм. Тогда становится очевидным: собирающие линзы отклоняют лучи к оптической оси, а рассеивающие линзы – от оптической оси. Параксиальные лучи (т.е. приосевые или околоосевые лучи, которые образуют с оптической осью малые углы), распространяющиеся параллельно главной оптической оси, после преломления сквозь линзу пересекаются в точке, лежащей на этой оси и называемой главным фокусом линзы. У всякой линзы имеются два фокуса по обе стороны от нее (точки F). Расстояние OF=f от оптического центра линзы до ее фокусов называется фокусным расстоянием линзы.
Величина, обратная фокусному расстоянию, называется оптической силой линзы (D=1/f ). Она измеряется в диоптриях (дптр или дп). 1 дптр – оптическая сила линзы с фокусным расстоянием 1 м (1 дптр = 1 м-1). В отличие от собирающей линзы (левый рисунок а)), рассеивающая линза имеет мнимые фокусы (правый рисунок б)). В мнимом фокусе сходятся (после преломления) воображаемые продолжения лучей, падающих на рассеивающуюся линзу параллельно главной оптической оси. Оптическая сила рассеивающей линзы, как ее фокусное расстояние, отрицательная величина.
Построение изображения (А1В1) предмета (АВ) в линзах осуществляется с помощью следующих лучей, ход которых нам известен: 1. лучи проходящие через оптический центр линзы не меняют своего направления (на рисунке, I луч); 2. лучи идущие параллельно главной оптической оси, после преломления в линзе (или его продолжение), проходят через второй главный фокус линзы (на рисунке, II луч); 3. лучи (или его продолжения), проходящие через первый главный фокус линзы, после преломления в ней, выходят из линзы параллельно ее главной оптической оси (на рисунке, III луч).
Пересечение любых двух таких лучей (или их продолжений) дает изображение точки предмета, откуда избранные лучи берут начало. Формула тонкой линзы имеет вид:
где a и b – соответственно расстояния от предмета и от его изображения до оптического центра линзы. Эту формулу самостоятельно можно получить, используя подобие треугольников: ΔВАО~ΔВ1 А1 О и ΔОСF~ΔB1 A1 F. Более сложный вид формулы тонкой линзы связывает фокусное расстояние f линзы с ее коэффициентом преломления n и радиусами R1 и R2 кривизны линзы (знак для радиусов кривизны линз берется положительный - для выпуклых поверхностей и отрицательный – для вогнутых) (см. приложения 2,3,4):
Так как фокусное расстояние рассеивающей линзы, как и ее оптическая сила, является отрицательной величиной, то это означает, что в формуле тонкой линзы a и b, в определенных случаях, должны иметь отрицательные значения. Правила, при помощи которых можно определить знаки a и b, в разных учебниках освещаются по-разному. Наиболее запоминающими, с моей точки зрения, являются правила, основанные на опыте повседневной жизни. Для этого надо только запомнить: · У собирающих линз f и D положительны, а у рассеивающих линз – отрицательны; · a всегда положительны; · b положительны, если изображения действительные, и отрицательны у мнимых изображений. Отношение линейных размеров изображения и предмета называется линейным увеличением линзы (А1В1/АВ). Отрицательным значением линейного увеличения соответствует действительное изображение (оно перевернутое), положительным – мнимое изображение (оно прямое). Нижеследующая таблица показывает характер изображения собирающей линзы в зависимости от расстояния предмета до линзы.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1032; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.113.185 (0.011 с.) |

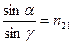
 , где
, где  и
и 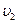 скорости света в I и II средах соответственно.
скорости света в I и II средах соответственно. .
. Если свет проходит из оптически более плотной среды (с показателем преломления n2) в оптически менее плотную среду (с показателем преломления n1 < n2 ), например из стекла или из воды в воздух (n1= 1), то угол падения будет меньше угла преломления γ. Поэтому при некотором угле падения (α = αпр.) угол преломления окажется равным 900 , т.е. преломленный луч будет скользить вдоль границы раздела сред, не выходя в первую среду. Угол αпр. называется предельным углом падения. При α > αпр. свет полностью отражается обратно во вторую среду (происходит полное внутреннее отражение света). При этом:
Если свет проходит из оптически более плотной среды (с показателем преломления n2) в оптически менее плотную среду (с показателем преломления n1 < n2 ), например из стекла или из воды в воздух (n1= 1), то угол падения будет меньше угла преломления γ. Поэтому при некотором угле падения (α = αпр.) угол преломления окажется равным 900 , т.е. преломленный луч будет скользить вдоль границы раздела сред, не выходя в первую среду. Угол αпр. называется предельным углом падения. При α > αпр. свет полностью отражается обратно во вторую среду (происходит полное внутреннее отражение света). При этом: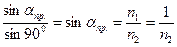



 Плоскость, проведенная через главный фокус линзы перпендикулярно к главной оптической оси, называется фокальной плоскостью. Лучи, падающие на линзу параллельно какой-либо побочной оптической оси, после преломления в линзе, пересекаются в точке, лежащей на фокальной плоскости (побочный или вторичный фокус, на рисунке точка F`). Т.е. фокальная плоскость является геометрическом местом всех вторичных фокусов. У линзы имеются две фокальные плоскости, расположенные на ровных расстояниях по обе стороны от нее.
Плоскость, проведенная через главный фокус линзы перпендикулярно к главной оптической оси, называется фокальной плоскостью. Лучи, падающие на линзу параллельно какой-либо побочной оптической оси, после преломления в линзе, пересекаются в точке, лежащей на фокальной плоскости (побочный или вторичный фокус, на рисунке точка F`). Т.е. фокальная плоскость является геометрическом местом всех вторичных фокусов. У линзы имеются две фокальные плоскости, расположенные на ровных расстояниях по обе стороны от нее.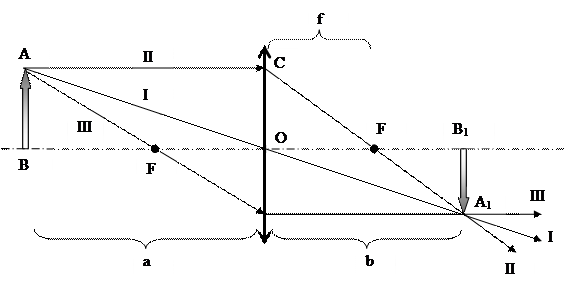
 ,
, .
.


