
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение предела последовательности.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Определение предела последовательности. число А называется пределом последовательности {Хn}, если для любого положительного Е существует номер n0, начиная с которого все члены последовательности отличаются от А по модулю меньше, чем на Е. Свойства пределов числовых последовательностей. 1)Сходящаяся последовательность имеет только один предел. 2) Сходящаяся последовательность ограничена. Мн-во чисел назыв. ограниченным, если сущ. такой отрезок [a,b] числовой оси, который содержит все числа из Х. 3)Если члены сход последовательности {Xn} удовлетворяют неравенству Xn>=b, то и lim Xn >= b
7. Правила вычисления пределов сходящихся последовательностей. 1) lim(Xn + Yn)= a+b 2) lim (Xn*Yn)=a*b 3)lim 1/Yn = 1/b, если у и б не равны 0 4) lim Xn/Yn= a/b
Определение ограниченной последовательности.
9.Определение бесконечно малой последовательности. Бесконечно малая последовательность — это последовательность, предел которой равен нулю.
10.Свойства бесконечно малых последовательностей. 1) Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью. 2)Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью. 3) Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью. 4)Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность. 5) Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. 6) Любая бесконечно малая последовательность ограничена. Определение беск. большой последовательности. Послед-ь {Xn} называется бб, если для любого положительного числа ε существует номер N такой, что при n > N выполняется неравенство |Xn| > ε. (lim (n→∞) Xn = ∞).
Свойства б.б.последовательностей. 1)б.б.последовательность является неограниченной. 2)Сумма б.б. и ограниченной послед-тей есть бесконечно большая послед-ть. 3)Сумма двух б.б. послед-тей одного знака есть б.б. того знака. 4)произведение б.б. послед-ти и ограниченной от нуля есть б.б. последовательность. Определение монотонных последовательностей. Последовательнсть {Хn} назыв.: возрастающей, если Хn<X(n+1) для всех n; невозрастающей, если Хn≤X(n+1) для всех n; убывающей, Хn>X(n+1) для всех n; неубывающей, Хn≥X(n+1) для всех n Определение предела функции в точке. Число а называется пределом функции f (x) в точке X0 (или пределом при X→ X0) если для любой сходящейся к точке X0 послед-и значений аргумента, отличных от X0, соответствующая послед-ь значений функции сходится к числу а, т. е. lim Xn = X0 (Xn ≠ X0) => lim f(Xn) = a; lim (X→ X0) f(x) = a. Свойства пределов функций. 1) Если 2)Если ф-ция f(x) имеет предел в точке X0, то в некоторой окрестности этой точки ф-ция ограничена,т.е. сущ-ет такая (проколотая) окрестность точки X0 и такое число А>0,что│f(x)│≤А для всех Х из этой окрестности 3) Если для всех точек Х некоторой окрестности точки Х0 выполняется неравенство f(x)≥b, то и limf(x)≥b, если только указанный предел существует. 4)Если в некоторой окрестности точки Х0 имеем f(x)≥g(x), то и limf(x)≥limg(x), если только указанные пределы сущ-ют. 5)Пусть в некоторой окрестности точки Х0 выполняются неравенства f(x)≥g(x)≥h(x),причём пределы f(x) и h(x) при Х→Х0 сущ-ют и равны между собой.Тогда предел g(x) при Х→Х0 также сущ-ет и равен тем пределам. Первый замечательный предел. lim (sinx/x) =1 при x→0 Второй замечательный предел Lim(1+ 1/n)n = e x→∞ 21. Дайте определения односторонних пределов функции в точке Число А называется правым пределом функции f(x) при х → а, если для любого ξ > 0 существует такое δ, что для всех х, удовлетворяющих неравенству а < х < а + δ, выполняется неравенство | f(x) - А |< ξ. Число А называется левым пределом функции f(x) при х → а, если для любого ξ > 0 существует такое δ, что для всех х, удовлетворяющих неравенству а - δ < х < а, выполняется неравенство | f(x) - А |< ξ. 1. Приведите примеры: а) послед-и, сходящейся к числу 3; б) ограниченной послед-и, не имеющей предела. Число а называется пределом числовой послед-и {Xn}, если для любого положительного числа ε существует номер N из множества Ñ такой, что для любого n ≥ N выполняется неравенство: | Xn – a | < ε √ ε > 0, сущ. N є Ñ, √ n ≥ N => | Xn – a | < ε А) Xn = (3n+1)/n, lim (n→∞) (3n+1)/n = 3 б) Xn = (-1)ⁿ - ограничена (-1), не имеет предела 2. Докажите, исходя из определения предела послед-и, что lim (n→∞) 2n/n+4 = 2. | Xn – a | < ε |2n/n+4 - 2| < ε, |-8/n+4| < ε, 8/n+4 < ε, n+4/8 >1/ε, n > (8 - 4ε)/ε, N = [8/ε - 4] +1 Уравнение касательной. Найдем ур-е касательной к графику Г ф-и y=f(x) в точке А(х0, f(x0)): т.к. т. А принадлежит Г и ур-ю касательной, то f(x0)=kx0+b, откуда b= f(x0)-kx0, значит, касательная задается след. Ур-м: y= kx+ f(x0)-kx0= f(x0)+k(х-x0) Т.к. k= f′(x0), то y=f(x0)+ f′(x0)(х-х0). Теорема Ролля. Если функция, непрерывна на отрезке [ a; b ] и дифференцируема на интервале (a; b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
Теорема Лагранжа. Пусть функция f (x) 1. непрерывна на отрезке [ a, b ]; 2. дифференцируема в интервале (a, b). Тогда существует точка с О (a, b) такая, что
Формула (1) называется формулой Лагранжа, или формулой конечных приращений Теорема Коши. Пусть даны две функции f(x) и g(x)такие, что: 1. f(x) и g(x)определены и непрерывны на отрезке 2. производные 3. производные 4. тогда
(Если убрать условие 4, то необоходимо усилить условие 3: g'(x) не должна обращаться в нуль нигде в интервале (a, b).) Правило Лопиталя. Теорема (правило Лопиталя). Пусть А – число, символ одностороннего предела (А=а±0) или символ бесконечности (А=±∞). Пусть функции ƒ(х) и g(х) либо обе бесконечно малые, либо обе бесконечно большие при х→А. Тогда, если существует предел
то существует и предел
при этом выполняется равенство:
Теорема Тейлора. Пусть функция f (x) имеет в точке x = a и некоторой ее окрестности производные порядка n+ 1. Тогда между точками a и x a найдется такая точка
Формула (10) называется формулой Тейлора, а выражение
представляет остаточный член в форме Лагранжа. Заметим, что если функция f (n+ 1)(x) ограничена в окрестности точки a, тогда остаточный член является бесконечно малой при x a более высокого порядка, чем (x-a) n. Таким образом, остаточный член можно записать в виде Rn+ 1(x) = o ((x-a) n) при x a. Данная форма записи остаточного члена называется формой Пеано. Формулой Маклорена называется формула Тейлора при a = 0:
Остаточный член в форме Пеано для формулы Маклорена имеет вид Rn+ 1 = o (xn) при x 0.
Найдите, исходя из определения, производную функции f(x) в точке x0: 26. f(x) = x3, x0 - произвольное число. Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’ (x)= f(x) = x3 f ′(xо)= 27. f(x)=sinx, xо-произвольное число Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’ (x)= f ′(xо)= 28. f (x)= Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’ (x)= f ’ (x)= 29. f(x)= Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’ (x)= f ’ (x)= 30. f(x)=x ½x½, x0=0 Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’ (x)=
31. Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’ (x)=
Найдите эластичность функции f (x) в точке x0: 38. f(x) = x4, x0 = 9. Эластичностью функции y = f(x) в точке х0 называется предел f (x) = x4 => E(x)= 39. f(x) = 3x, x0 = 5. Эластичностью функции y = f(x) в точке х0 называется предел E(x)= 40. Докажите, что эластичность произведения двух функций равна сумме их эластичностей.  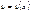 и и  в точке в точке 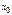 равна сумме эластичностей ф-ций в этой же точке: равна сумме эластичностей ф-ций в этой же точке:  . Эластичность равна Ey=x(lny) . Эластичность равна Ey=x(lny)
 тогда тогда   . .
42. Сформулируйте теорему Ролля. Можно утвержд, что производная функции f(x) = (x-2)(x-3)(x-4)(x-5) обращается в нуль в трех точках интервала (2,5)? Пусть ф-ция Можно. f(2)=0, f(3)=0, f(4)=0, f(5)=0 => существует С1из (2;3), такое, что f'(C1)=0, и тд 2, 3, 5, 4 43. Сформулируйте теорему Лагранжа. Докажите, что если f ′(x) = 0 на интервале (a,b), то функция f (x) постоянна на этом интервале. Пусть функция f(x) 1. непрерывна на отрезке [a, b]; 2. дифференцируема в интервале (a, b). Тогда существует точка с О (a, b) такая, что f(b) − f(a) = f '(c) · (b − a)
Формула Ньютона-Лейбница. Для нахождения определенного интеграла для функции f(x), интегрируемой на отрезке[a,b ]: Определение предела последовательности. число А называется пределом последовательности {Хn}, если для любого положительного Е существует номер n0, начиная с которого все члены последовательности отличаются от А по модулю меньше, чем на Е.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 832; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.99.39 (0.007 с.) |

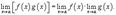 Ограниченная последовательность (ограниченная с обеих сторон последовательность) — это последовательность, ограниченная и сверху, и снизу. Ограниченная сверху последовательность — это последовательность элементов множества X, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности. Ограниченная снизу последовательность — это последовательность элементов множества X, для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.
Ограниченная последовательность (ограниченная с обеих сторон последовательность) — это последовательность, ограниченная и сверху, и снизу. Ограниченная сверху последовательность — это последовательность элементов множества X, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности. Ограниченная снизу последовательность — это последовательность элементов множества X, для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.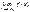 существует, то он единственный.
существует, то он единственный. ;
;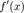 и
и 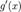 конечны на интервале
конечны на интервале  ;
; и
и  не обращаются в нуль одновременно на интервале
не обращаются в нуль одновременно на интервале  ;
; , где
, где 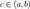
 (конечный или бесконечный),
(конечный или бесконечный),

 , что справедлива следующая формула:
, что справедлива следующая формула: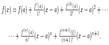
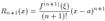

 Приведем разложения некоторых элементарных функций по формуле Маклорена
Приведем разложения некоторых элементарных функций по формуле Маклорена
 =
= 
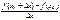

 = =
= = 
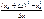 =
= 
 =3
=3 
 =
= 
 =
=  = cosx0
= cosx0 , xо =9
, xо =9

 =
=  =1/6
=1/6 , xо =1
, xо =1
 =
=  =
=  =
=  =-2
=-2 =
= 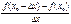

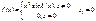
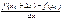

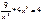 , при x0 = 9.
, при x0 = 9.

 непрерывна на отрезке [a;b], дифференцируема на интервале (a;b) и
непрерывна на отрезке [a;b], дифференцируема на интервале (a;b) и  , то найдётся хотя бы одна точка
, то найдётся хотя бы одна точка  , в которой
, в которой 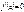 .
.
 =>
=> 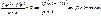
 , гдеF(x)- любая первообразная для функции f(x) на[a,b].
, гдеF(x)- любая первообразная для функции f(x) на[a,b].


