Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический смысл производной.Содержание книги Поиск на нашем сайте Пусть Г- график функции y=f(x). Рассмотрим на Г т. А(x0,f(x0)) и т. В (x0+Δx,f(x0+Δx)) Прямая АВ называется секущей. Будем считать, что y=f(x)-непрерывная функция, тогда если Δх→0, то f(x0+Δx)→f(x0), т.е. В→А при Δх→0. Пусть γ – угол наклона секущей относительно оси ОХ. Если существует предел lim γ=γ0 при Δх→0, то прямая, проходящая через А и образующая с осью ОХ угол γ0, называется касательной к Г в точке А. Пусть С(f(x0+Δх), f(x0)) – точка, дополняющая отрезок АВ до прямоуг. треугольника АВС. Т.к. АС//ОХ, то tgγ =Δу/Δх. Переходя к пределу, получим: tgγ0=f′(x0) Т.е. геометрический смысл производной состоит в том, что f′(x0) – это тангенс угла наклона касательной к графику y=f(x) в точке (x0,f(x0)). Уравнение касательной. Найдем ур-е касательной к графику Г ф-и y=f(x) в точке А(х0, f(x0)): т.к. т. А принадлежит Г и ур-ю касательной, то f(x0)=kx0+b, откуда b= f(x0)-kx0, значит, касательная задается след. Ур-м: y= kx+ f(x0)-kx0= f(x0)+k(х-x0) Т.к. k= f′(x0), то y=f(x0)+ f′(x0)(х-х0). Определение эластичности функции. функции y = f(x) в точке х0 называется следующий предел Eyx(x0) = lim ((Δy/y): (Δx/x)). Δx ® 0 Эластичность Ey – это коэффициент пропорциональности между относительными изменениями величин y и x.) Теорема Ролля. Если функция, непрерывна на отрезке [ a; b ] и дифференцируема на интервале (a; b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
Теорема Лагранжа. Пусть функция f (x) 1. непрерывна на отрезке [ a, b ]; 2. дифференцируема в интервале (a, b). Тогда существует точка с О (a, b) такая, что
Формула (1) называется формулой Лагранжа, или формулой конечных приращений Теорема Коши. Пусть даны две функции f(x) и g(x)такие, что: 1. f(x) и g(x)определены и непрерывны на отрезке 2. производные 3. производные 4. тогда
(Если убрать условие 4, то необоходимо усилить условие 3: g'(x) не должна обращаться в нуль нигде в интервале (a, b).) Правило Лопиталя. Теорема (правило Лопиталя). Пусть А – число, символ одностороннего предела (А=а±0) или символ бесконечности (А=±∞). Пусть функции ƒ(х) и g(х) либо обе бесконечно малые, либо обе бесконечно большие при х→А. Тогда, если существует предел
то существует и предел
при этом выполняется равенство:
Производные и дифференциалы высших порядков. Если для функции y=f(x) определена производная у(к-1) порядка (к-1), то производную у(к) порядка к (при условии ее существования) определяют как производную от производной порядка (к-1), т.е. у(к) = (у(к-1))′. В частности, у’’=(y’)’- производная второго порядка, y’’’=(y’’)’ – третьего и т.д.
Дифференциалы высших порядков ф-и y=f(v) последовательно определяются таким образом: d2y=d(dy) – диф-л 2-го порядка d3y=d(d2y)… dny=d(d n-1 y) - диф-л n-го порядка Формула Тейлора. Формула Маклорена. Теорема Тейлора. Пусть функция f (x) имеет в точке x = a и некоторой ее окрестности производные порядка n+ 1. Тогда между точками a и x a найдется такая точка
Формула (10) называется формулой Тейлора, а выражение
представляет остаточный член в форме Лагранжа. Заметим, что если функция f (n+ 1)(x) ограничена в окрестности точки a, тогда остаточный член является бесконечно малой при x a более высокого порядка, чем (x-a) n. Таким образом, остаточный член можно записать в виде Rn+ 1(x) = o ((x-a) n) при x a. Данная форма записи остаточного члена называется формой Пеано. Формулой Маклорена называется формула Тейлора при a = 0:
Остаточный член в форме Пеано для формулы Маклорена имеет вид Rn+ 1 = o (xn) при x 0.
Найдите, исходя из определения, производную функции f(x) в точке x0: 26. f(x) = x3, x0 - произвольное число. Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’ (x)= f(x) = x3 f ′(xо)= 27. f(x)=sinx, xо-произвольное число Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’ (x)= f ′(xо)= 28. f (x)= Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’ (x)= f ’ (x)= 29. f(x)= Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’ (x)= f ’ (x)= 30. f(x)=x ½x½, x0=0 Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’ (x)=
31. Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’ (x)=
Найдите эластичность функции f (x) в точке x0: 38. f(x) = x4, x0 = 9. Эластичностью функции y = f(x) в точке х0 называется предел f (x) = x4 => E(x)= 39. f(x) = 3x, x0 = 5. Эластичностью функции y = f(x) в точке х0 называется предел E(x)= 40. Докажите, что эластичность произведения двух функций равна сумме их эластичностей.  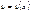 и и  в точке в точке 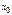 равна сумме эластичностей ф-ций в этой же точке: равна сумме эластичностей ф-ций в этой же точке:  . Эластичность равна Ey=x(lny) . Эластичность равна Ey=x(lny)
 тогда тогда   . .
42. Сформулируйте теорему Ролля. Можно утвержд, что производная функции f(x) = (x-2)(x-3)(x-4)(x-5) обращается в нуль в трех точках интервала (2,5)? Пусть ф-ция Можно. f(2)=0, f(3)=0, f(4)=0, f(5)=0 => существует С1из (2;3), такое, что f'(C1)=0, и тд 2, 3, 5, 4 43. Сформулируйте теорему Лагранжа. Докажите, что если f ′(x) = 0 на интервале (a,b), то функция f (x) постоянна на этом интервале. Пусть функция f(x) 1. непрерывна на отрезке [a, b]; 2. дифференцируема в интервале (a, b). Тогда существует точка с О (a, b) такая, что f(b) − f(a) = f '(c) · (b − a)
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 832; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 ;
;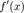 и
и 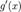 конечны на интервале
конечны на интервале  ;
; и
и  не обращаются в нуль одновременно на интервале
не обращаются в нуль одновременно на интервале  ;
; , где
, где 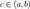
 (конечный или бесконечный),
(конечный или бесконечный),

 , что справедлива следующая формула:
, что справедлива следующая формула: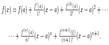
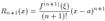

 Приведем разложения некоторых элементарных функций по формуле Маклорена
Приведем разложения некоторых элементарных функций по формуле Маклорена
 =
= 
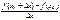

 = =
= = 
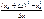 =
= 
 =3
=3 
 =
= 
 =
=  = cosx0
= cosx0 , xо =9
, xо =9

 =
=  =1/6
=1/6 , xо =1
, xо =1
 =
=  =
=  =
=  =-2
=-2 =
= 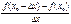

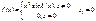
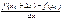

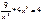 , при x0 = 9.
, при x0 = 9.

 непрерывна на отрезке [a;b], дифференцируема на интервале (a;b) и
непрерывна на отрезке [a;b], дифференцируема на интервале (a;b) и  , то найдётся хотя бы одна точка
, то найдётся хотя бы одна точка  , в которой
, в которой 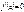 .
.
 =>
=>