
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение бесконечно большой функции.Содержание книги Поиск на нашем сайте
Функцию ( Первый замечательный предел. lim (sinx/x) =1 при x→0 Второй замечательный предел Lim(1+ 1/n)n = e x→∞ 21. Дайте определения односторонних пределов функции в точке Число А называется правым пределом функции f(x) при х → а, если для любого ξ > 0 существует такое δ, что для всех х, удовлетворяющих неравенству а < х < а + δ, выполняется неравенство | f(x) - А |< ξ. Число А называется левым пределом функции f(x) при х → а, если для любого ξ > 0 существует такое δ, что для всех х, удовлетворяющих неравенству а - δ < х < а, выполняется неравенство | f(x) - А |< ξ. 1. Приведите примеры: а) послед-и, сходящейся к числу 3; б) ограниченной послед-и, не имеющей предела. Число а называется пределом числовой послед-и {Xn}, если для любого положительного числа ε существует номер N из множества Ñ такой, что для любого n ≥ N выполняется неравенство: | Xn – a | < ε √ ε > 0, сущ. N є Ñ, √ n ≥ N => | Xn – a | < ε А) Xn = (3n+1)/n, lim (n→∞) (3n+1)/n = 3 б) Xn = (-1)ⁿ - ограничена (-1), не имеет предела 2. Докажите, исходя из определения предела послед-и, что lim (n→∞) 2n/n+4 = 2. | Xn – a | < ε |2n/n+4 - 2| < ε, |-8/n+4| < ε, 8/n+4 < ε, n+4/8 >1/ε, n > (8 - 4ε)/ε, N = [8/ε - 4] +1 Докажите, что сходящаяся послед-ь имеет только один предел От противного Предп, что некоторая послед-ь {Xn} имеет 2 разл предела а и b, a ≠ b. Выберем столь малые окрестности т. a и b, чтобы они не имели общ точек. Т.к. lim Xn = a, все Xn, начиная с нек номера n1, содержатся в выбран окрестности т. а; точно так же из lim Xn = b, следует, что все Xn, начиная с нек номера n2, содержатся в выбранной окрестности т. b. Положим, n0 = max {n1, n2}. Тогда числа Xn с номерами n≥ n0 должны принадлежать как первой, так и второй окрестности, что невозможно, так как окрестности не имеют общих точек. Докажите ограниченность сход послед-и док-во: Пусть lim Xn = a. Положим ε = 1 и найдем номер n0, начиная с которого | Xn – a | < 1, т. е. -1>Xn – a<1 для n≥ n0. Отсюда следует а-1>Xn<а+1 для всех n≥ n0. Заменим отрезок [а-1; а+1] таким отрезком [А;В], чтобы в него попали не только числа Xn, n≥ n0, но и все числа х1, х2,…хn0. Тогда будем иметь хn є [А;В] для всех n є N, что означает ограниченность множества {Хn}. 5. Дайте определение послед-и, ограниченной сверху. Может ли предел послед-и, ограниченной снизу числом 6, быть равным: а) 5,98; б) 6,02 Послед-ь называется ограниченной сверху, если существует число m, такое, что любой элемент Xn этой послед-и удовлетворяет неравенству m ≥ Xn. Предел послед., огранич. сверху числом 6, не может быть равным 6,02, но может быть равным 5,98, так как мы можем брать только числа меньше 6 (6≥Xn). 6. Что можно сказать о пределе суммы двух сходящихся послед-ей? Приведите пример расходящихся послед-ей, сумма которых сходится. 1) Алгебраическая сумма двух сходящихся послед-ей {Хn} и {Уn} есть сходящаяся послед-ь, предел которой равен сумме пределов послед-ей {Хn} и {Уn}. lim (n→∞) Xn = a, lim (n→∞) Уn = b: lim (n→∞) (Xn + Уn) = a + b. 2) an = (-1)ⁿ: -1; 1; -1; 1…- расход. bn = (-1)^(n+1): 1; -1; 1; -1…- расход. lim (n→∞) (an + bn) = 0 7. Что можно сказать о пределе произведения двух сходящихся послед-ей? Приведите пример расходящихся послед-ей, произведение которых сходится. 1) Произведение двух сходящихся послед-ей {Хn} и {Уn} есть сходящаяся послед-ь, предел которой равен произведению пределов послед-ей {Хn} и {Уn}. lim (n→∞) Xn = a, lim (n→∞) Уn = b: lim (n→∞) (Xn * Уn) = a * b. 2) an = (-1)ⁿ: -1; 1; -1; 1…- расход. bn = -1/2, 1/2, -2/3, 2/3, -3/4, 3/4: (-n/ n + 1)ⁿ lim (n→∞) (an * bn) = 1 – сход. (1/2, 1/2, 2/3, 2/3…). 8. Может ли послед-ь {Xn + Yn} сходиться, если послед-ь {Xn} сходится, а послед-ь {Yn} расходится? Ответ обоснуйте. нет, не может: С + ∞ = ∞ Xn = (1/2)ⁿ: 1/2, 1/4… Yn = (-1)ⁿ: -1, 1.. -1 + ½ = -1/2; -1 + 1/8 = -7/8 – сход. к (-1) 1 + ¼ = 1 ¼; 1 + 1/16 = 1 1/16 – сход. к 1 {Xn + Yn} – расход. 9. Дайте определение бесконечно малой (бм) послед-и. Приведите примеры бм послед-ей, отношение которых: а) является бм послед-ью; б) не является бм послед-ью. Послед-ь {αn} называется бм, если lim (n→∞) αn = 0. Для любого ε > 0, сущ. N, такое, что для любого n ≥ N | αn | < ε. а) 1/n, 1/ ^4√n – бм послед-и: ^4√n/ n = n^-3/4 – бм послед-ь б) n/ ^4√n = n^3/4 - не бм послед-ь Докажите, что произведение бм и ограниченной послед-ей является бм послед-ью. док-во: Пусть {Хn} – ограниченная, а {αn} – бм послед-и. Доказать, что {Xn * αn} – бм. Так как {Хn} ограниченна, то существует число А > 0 такое, что любой элемент Хn удовлетворяет неравенству | Хn | ≤ А. Возьмем любое ε > 0. Поскольку {αn} – бм, то для положительного числа ε/А существует номер N такой, что при n > N выполняется неравенство | αn | < ε/А. Тогда при n > N |Xn * αn | = |Xn| * | αn | < A * ε/A = ε. Это означает, что послед-ь {Xn * αn} – бм.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.63.148 (0.008 с.) |

 называют бесконечно большой приХ, стремящемся к Х0, если для любой последовательности
называют бесконечно большой приХ, стремящемся к Х0, если для любой последовательности 
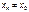 )значений аргумента, стремящейся к Х0,соответствующая последовательность значений функции
)значений аргумента, стремящейся к Х0,соответствующая последовательность значений функции  является бесконечно большой. Записывают:
является бесконечно большой. Записывают:  .
.


